GNSS(二):融合策略
文章目录
- 一、背景
- 二、松耦合融合策略
-
- 1. 信息有效性判断
- 2. 坐标系对齐
- 3. 观测方程
-
- a.杆臂补偿
- b.速度融合
- c.位置融合
-
- 1) 置信度设置
- d. 航向yaw融合
- 4.观测性分析
-
-
- 1)状态表示在VIO坐标系下的观测性分析
- 2)状态表示在GPS ENU坐标系下的观测性分析
-
- 三、紧耦合融合
-
- 1. 系统状态向量
- 2.基础知识
- 3.观测方程
-
- a. 伪距观测噪声
- b.伪距观测方程
- c.伪距Jacobian 计算
- d.多普勒测速噪声
- e.观测方程
- f. Jacobian推导
- g. Receiver Clock观测
- h.高精RTK定位(载波相位观测)
- i.初始化
- i.实验效果
一、背景
前面介绍了GNSS的定位原理,那么正常的GNSS模组可以解算出位置 ( G x , G y , G z ) (^Gx, ^Gy,^Gz) (Gx,Gy,Gz)以及三维速度 ( G v x , G v y , G v z ) (^Gv_x,^G v_y, ^Gv_z) (Gvx,Gvy,Gvz)以及航向角度yaw,同时也可以输出原始的GNSS测量,本文主要介绍滤波系统如何融合这些观测。
直接融合原始测量我们叫做紧耦合融合,而融合解算位姿速度结果的叫做松耦合融合。
二、松耦合融合策略
我们将坐标系转到GPS坐标系,我们这里将GPS坐标系标记为G. 变换前VIO的世界坐标系为VIO坐标系,并不是ENU,和GPS存在4 dof外参。
1. 信息有效性判断
RTK和GPS主要就是通过是否进入固定解,以及位置速度的置信度参数决定;双天线yaw的置信度也是一样,此外双天线可以判断一下解算的base_line和已知测量的baseline做个比较,或者求解的roll角度和当前飞机估计的角度作比较,去掉一些错误观测,相近才认为yaw准确。
2. 坐标系对齐
这里其实就是求解一个SE(3)的变换,求解 T w g p s T^{gps}_{w} Twgps坐标系变换,然后把w坐标系转成GPS坐标系即可。
求解方式很多,简单点可以直接建立一个小的优化问题,求解偏差即可,快一点的话就建立一个滤波器,滤波坐标变换偏差,cov收敛即为完成收敛。此外,初始化时,建议先初始化yaw(可以直接通过双天线,也可以通过速度对齐计算yaw),再计算位置。
3. 观测方程
a.杆臂补偿
GPS/IMU融合中的杆臂补偿是为了将IMU测量的姿态和加速度数据与GPS测量的位置数据进行一致性对齐。由于IMU和GPS通常安装在移动平台上的不同位置,导致IMU和GPS测量的参考点存在一定的偏移,因此需要进行杆臂补偿。主要是转弯时,刚体速度需要补偿。

v g p s = v i m u + b × w v_{gps} = v_{imu}+b\times w vgps=vimu+b×w,后文用到的杆臂为 t g p s i m u t_{gps}^{imu} tgpsimu。
杆臂补偿的原理是通过将IMU测量数据转换到与GPS天线在同一位置的参考点上,实现IMU和GPS数据的对齐。具体步骤如下:
-
确定杆臂向量:通过测量或者通过精确的安装参数来获取IMU测量点与GPS天线之间的距离和方向差异,得到杆臂向量b = [b_x, b_y, b_z]。
-
转换IMU测量数据:将IMU测量的加速度和角速度数据转换到与GPS天线在同一位置的参考点上。这可以通过将IMU测量数据与杆臂向量进行叉乘来实现。
-
- 加速度补偿:将IMU测量的加速度数据a_imu = [a_x_imu, a_y_imu, a_z_imu]转换为a_gps = [a_x_gps, a_y_gps, a_z_gps],其中a_gps = a_imu + b × w_imu,w_imu为IMU测量的角速度数据。
-
- 角速度补偿:将IMU测量的角速度数据w_imu = [w_x_imu, w_y_imu, w_z_imu]转换为w_gps = [w_x_gps, w_y_gps, w_z_gps],其中w_gps = w_imu。
-
融合IMU和GPS数据:将补偿后的IMU数据与GPS数据进行融合
b.速度融合
坐标系对齐之后W世界坐标系和GPSbase坐标系E对齐,我们后续都用W表示。观测方程如下:
r = w v g p s m e a s − w v g p s = w v m e a s − ( R i w s k e w ( w m e a s − b g ) t g p s i m u + w v ) r = ^wv_{gps_{meas}}- ^wv_{gps}=^wv_{meas}-(R_i^wskew(w_{meas} - b_g)t_{gps}^{imu}+^wv) r=wvgpsmeas−wvgps=wvmeas−(Riwskew(wmeas−bg)tgpsimu+wv)
c.位置融合
r = w p g p s m e a s − w p g p s = w p m e a s − ( R i w t g p s i + w t i ) r = ^wp_{gps_{meas}}- ^wp_{gps} =^wp_{meas}-(R_i^wt_{gps}^{i}+^wt_i) r=wpgpsmeas−wpgps=wpmeas−(Riwtgpsi+wti)
1) 置信度设置
前面提到,GNSS的本质是求解以下一个四元非线性方程组

观测:
- 接收机伪距
- 卫星位置
待求量: - 接收机位置
- 接收机时钟钟差
至少需要4个卫星观测才能求解。首先原始的伪距测量我们可以根据视角、卫星和接收机噪声设置其观测噪音,那么也可以将其转化为xyz的噪音,基本思想就是将上述非线性方程线性化,计算出线性变换矩阵,然后根据这个矩阵转换计算xyz的噪声即可。
y m = f ( x ) = f ( x 0 ) + G δ x + n y^m=f(x)=f(x_0)+G\delta x+n ym=f(x)=f(x0)+Gδx+n
b = y m − f ( x 0 ) = G δ x + n b=y^m-f(x_0)=G\delta x+n b=ym−f(x0)=Gδx+n
设:

这里r对接收机位置x轴求解:

这个结果是一个单位观测方向矢量的x轴分量。

类似的, r n r^n rn相对于xyz的导数为:
![]()
线性化之后:

其中:


上式考虑噪声:
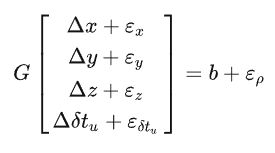
求逆变换得到:

进而得到噪声传播关系:

这样得到cov的转换关系:

这里xyz还是经纬高,需要转化为ENU坐标系下,变换矩阵为S:

所以最终ENU坐标系下的位置测量方差为:
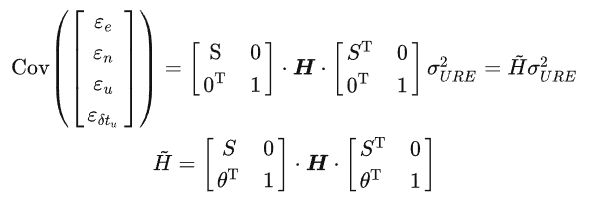
这样我们就可以得到xyz的置信度了,作为松耦合融合的置信度参数。可以看到,这个参数和下面两个因素有关:
1、测量误差:伪距测量误差的方差越大,则定位误差的方差也就越大;
2、卫星的几何分布:矩阵G和H取决于可见卫星的个数及其相对于用户的几何分布,所以卫星的个数和分布直接影响最终xyz的解算精度。
d. 航向yaw融合
相对位置和速度融合,航线融合有一定的技巧,主要是一般状态变量中不会维护yaw,而是维护3dof的so(3)。
当前状态的R转成欧拉角Euler,观测方程为:
r = y a w m e a s − E u l e r [ 0 ] r = yaw_{meas} - Euler[0] r=yawmeas−Euler[0]
下面主要介绍解析求解Jacobian矩阵时如何计算。即欧拉角关于so(3)的Jacobian矩阵。
四元数转旋转矩阵公式:
![]()
此外,一些基础公式,主这里使用JPL左手系四元数表示(Global到Local)


带入四元数转旋转公式得到
![]()
因此

此外还会用到反对称矩阵这个公式:

旋转矩阵转欧拉角如下:
![]()
<相对于固定坐标系,旋转矩阵按旋转顺序左乘,右乘是相对动坐标系>
忽略二阶项得到:

进而可以得到扰动项为

这里H就是R关于欧拉角求导的Jacobian矩阵,这样就可以进行covariance的转换:
![]()
要求解的 J = ∂ E u l e r ∂ R = ∂ R ∂ E u l e r . i n v e r s e ( ) = H T J=\frac{\partial Euler}{\partial R} = \frac{\partial R}{\partial Euler} .inverse()=H^T J=∂R∂Euler=∂Euler∂R.inverse()=HT的第三行;关于roll,pitch求导也是一样,取第一和第二行即可。
4.观测性分析
观测性分析是滤波系统中常用的问题分析方式,如常见的VIO系统4自由度不可观等,都可以通过观测性分析得到,我们简单介绍一下融合GPS之后系统的观测性(虽然结论显而易见,全部可观,这里就是理论推导一下)。后面有时间单独写一个如何进行观测性推导的内容,这里一些基础概念就不多做介绍了。
系统的可观性(observability)是指能否通过系统的输出来完全确定系统的内部状态。一个可观性良好的控制系统意味着系统的所有状态变量都可以通过测量系统的输出来准确地估计或恢复出来。
1)状态表示在VIO坐标系下的观测性分析
IMU的error state transition matrix为:

我们使用transition matrix去propagate covariance matrix。
![]()
这里V表示正常VIO系统的世界坐标系,E表示GPS的世界坐标系,第一种我们假设状态都表示在VIO的世界坐标系V,状态向量为:
![]()
注:这里VIO坐标系也是水平的,所以 V E R ^E_VR VER只有1个自由度。
视觉重投影和GPS观测的*观测方程**为:

线性化之后的预测和观测方程可以表示为

这里的state transition matrix为:

视觉观测方程对状态求解H矩阵为:

GPS观测对应H矩阵为:

合并在一起的观测矩阵为:

进而可以得到观测性矩阵为:

可以看到这个矩阵的零空间为:

一般这种零空间都比较显而易见,很容易就能拼凑出来,但是,也可以通过下面的方法判断是哪个状态的零空间。
V x + x ~ = V ′ x ^Vx + \tilde x = ^{V'}x Vx+x~=V′x
这里求出 x ~ \tilde x x~,然后看是不是零空间,是的话,就是这个方向不可观。以绕g重力旋转为例,我们增加扰动 V V ′ R = I + ⌊ α g × ⌋ ^{V'}_VR = I+\left \lfloor \alpha g\times \right \rfloor VV′R=I+⌊αg×⌋,求出 x ~ \tilde x x~即可。

以外参项 V E R ^E_V\textbf{R} VER为例,得到其 x ~ \tilde x x~

特征位置对应扰动为

因此,初始条件的扰动 V V ′ R = I + ⌊ α g × ⌋ ^{V'}_VR = I+\left \lfloor \alpha g\times \right \rfloor VV′R=I+⌊αg×⌋能够变成状态的扰动,而这个扰动就是我们的零空间,所以说明绕重力旋转不可观

2)状态表示在GPS ENU坐标系下的观测性分析
此时系统坐标系为ENU坐标系,我们标志为E

此时观测性矩阵为:

对比前面的观测性矩阵:

很明显前面的零空间 n u l l ( v M ) null(^vM) null(vM)不再是 E M ^EM EM的零空间,但他有新的零空间,还是4个自由度,主要是因为我们把GPS到VIO的4dof外参放在了状态变量中,边缘化这4dof状态,就会发现状态完全可观了。
三、紧耦合融合
1. 系统状态向量

在VINS的基础上增加了几个变量:
1) Ψ \Psi Ψ:local world(yaw未和ENU对齐)和ENU系之间的偏航角。
2) δ t \delta \textbf{t} δt:接收机时钟钟差。因为GVINS支持四个导航系统——GPS、GLONASS、Galileo和北斗卫星,不同的导航系统相应的接收机钟差是不同的。
3) δ t ˙ \delta \dot{t} δt˙:接收机时钟钟差变化率只有一个,不同导航系统是相同的。
2.基础知识
全球导航卫星系统(GNSS)有四个独立且完全运行的GNSS系统,即GPS、GLONASS、伽利略和北斗。每个GNSS系统中的导航卫星不断广播无线电信号,接收器可以从中唯一识别卫星并检索导航信息。以GPS L1C信号为例,最终传输的信号由三层组成,如下图所示。导航信息包含轨道参数、时钟误差的校正、电离层延迟的系数以及与卫星状态相关的其他信息。
- 轨道参数,也称为星历,包含14个变量,用于计算卫星在特定时间的地心地固坐标(ECEF coordinates)。
- 卫星的时钟误差被建模为二阶多项式,即,有三个参数。
每颗卫星都被分配一个每1毫秒重复一次的唯一伪随机噪声(PRN)码。首先将50位/秒的导航信息与PRN码进行异或操作,然后用它来调制高频载波信号。接收到信号后,接收器通过测量它和设计信号之间的频率差来获得多普勒偏移。从PRN码偏移(表示传播时间)中推断出伪距测量,最后,通过反向解调过程解析出导航信息。

卫星方面的误差源主要由卫星轨道(星历)和卫星钟差组成。轨道误差来自其他天体的影响,这些天体并未被星历精确建模,时钟误差是卫星上不完美的原子钟相对于标准系统时间的结果。轨道和时钟误差由系统控制段进行监控并不断校正。当信号到达时,通过比较由卫星的原子钟标记的信号传输时间和接收器的较不准确的本地时钟时间,计算飞行时间。
-
伪距测量可以模型化为,前一篇文章详细介绍过:

前面两个 p p p分别是卫星和接收机在ECI coordinates下的位置, ς s \varsigma_s ςs是4*1的向量,用1记录了当前导航系统的是否使用, △ t s \bigtriangleup t^s △ts为卫星钟差,随后就是对流层和电力层延迟,多径和噪声(单位×c统一到m). -
多普勒测量:多普勒频率偏移是通过接收到的载波信号和设计的信号之间的差异来测量的,它反映了接收器-卫星沿信号传播路径的相对运动。由于GNSS信号结构的特性,多普勒测量的精度通常比伪距的精度高一个数量级。

前面两个 v v v分别是卫星和接收机在ECI coordinates下的速度, λ \lambda λ表示载波信号的波长, κ r s \kappa_r^s κrs为从接收器到卫星的单位向量,表示在ECI coordinates, δ t ˙ \delta \dot{t} δt˙:接收机时钟钟差变化率, △ t ˙ s \bigtriangleup \dot t^s △t˙s为卫星的钟差变化率,最后一项是噪音。
3.观测方程
a. 伪距观测噪声
伪距测量的噪声模型符合均值为0的高斯分布:
![]()
其中标准差为:
![]()
其中 n s n_s ns 是广播卫星空间精度指标; n p r n_{pr} npr接收机上报的伪码测量噪声指标; θ e l \theta_{el} θel卫星在接收机视野中的仰角。这个分母项有两个原因。首先,它可以抑制由GNSS多径效应引起的噪声,这种效应通常出现在低仰角的卫星上。其次,由导航系统广泛采用的Klobuchar模型得到的电离层延迟,仍然包含高达50%的误差, 由于低仰角的卫星会受到显著的电离层延迟,分母项也可以减少电离层补偿带来的误差。
b.伪距观测方程
ENU系到ECEF系的转换:纬度 λ \lambda λ,经度 ϕ \phi ϕ

local world系和ENU系只差一个偏航角 ψ \psi ψ ,那么local world系到ENU系的转换为
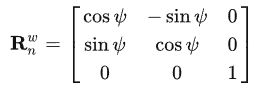
则接收机在local world下的坐标和ECEF下的坐标关系转换为
n: ENU坐标系
e:ECEF坐标系
![]()
这里涉及先选择一个anchor point的问题,可以通过SPP粗糙的估计anchor point位置,选定anchor point的LLA,作为ECEF和ENU坐标系之间的转换原点(因此也可以求出锚点处ENU转ECEF的旋转),并在初始化的时候调整local frame的轨迹和ECEF系下的对齐。这样anchor point从之前ENU系的原点变为local frame系的原点。对应松耦合的坐标系对齐过程。
p r w − p a n c w \textbf{p}_r^w-\textbf{p}_{anc}^w prw−pancw是在local world系下接收机位置到anchor point点的向量差,其中,设置local world系的坐标系原点是anchor point,又因为ENU的中心和local world的中心重合,所以 p a n c w \textbf{p}_{anc}^w pancw是0。 R n e R w n ( p r w − p a n c w ) \textbf{R}^e_n\textbf{R}^n_w(\textbf{p}_r^w-\textbf{p}_{anc}^w) RneRwn(prw−pancw)将向量差变换到了ECEF系下;即:
![]()
移项变换,即可得到公式(14)中接收机在ECEF下的位置坐标 p r e \textbf{p}_r^e pre.
接收机天线和机体坐标系的变换为:

定义E坐标系与接受到信号时间的ECEF一致,那么:
![]()
这里信号离开时的卫星位置和接受时候的卫星位置不一样,需要考虑信号传输时间 t f t_f tf和地球转速进行补偿。
![]()
最终,伪距测量误差因子可以建模为:
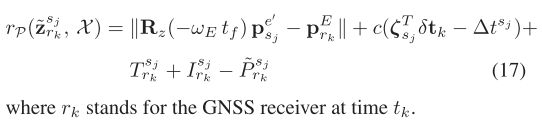
为避免混淆,接受时刻ECI我们不用E,也用e表示:

再将(14)(15)带入,得到:
注:这里为了方便推导,近似机体b和接收机r重合:

因此:

这里卫星位置,卫星的钟差、电离层误差可以计算得到,对流层误差也可通过建立适当的模型进行估计。anchor point在ECI系下的位置可以计算出来,因相关联的状态变量只有:
![]()
我们近似机体b和接收机r重合,那么 q b w \textbf{q}_b^w qbw就也没有了。
c.伪距Jacobian 计算
伪距测量误差对 p b t k w \textbf{p}^w_{b_{t_k}} pbtkw的导数
设:
![]()

伪距测量误差对 ψ \psi ψ的导数

其中 R w n \textbf{R}^n_w Rwn为:
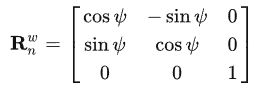
导数为:

**伪距测量误差对 δ t k \delta \textbf{t}_k δtk**的导数为:

d.多普勒测速噪声
η r s \eta_r^s ηrs是多普勒频移噪声,服从均值为0的高斯分布,其均方差建模为:

其中 n s n_s ns 是广播卫星空间精度指标; n d p n_{dp} ndp为接收机的测量噪声; θ e l \theta_{el} θel卫星在接收机视野中的仰角。
e.观测方程
前面提到,多普勒频率偏移为:

同样,这里e为接收时刻的ECEF坐标系,是一个ECI坐标系, v s e \textbf{v}^e_s vse v r e \textbf{v}^e_r vre分别是卫星和接收机在ECEF系下的速度, λ \lambda λ表示载波信号的波长, κ r s \kappa_r^s κrs是在ECEF下接收器到卫星的单位观测向量:

其实就是为了计算速度差在伪距方向的投影。残差为:
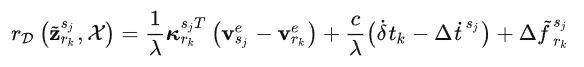
接收机在接受时刻ECEF系下的速度和在local world中的速度之间的转换为:
![]()
![]()
同样假设机体b和接收机r重合,则相关联的系统状态为:
![]()
f. Jacobian推导
多普勒频移误差对 v b t k w \textbf{v}^w_{b_{t_k}} vbtkw的导数

多普勒频移误差对 ψ \psi ψ的导数

多普勒频移误差对 δ t ˙ k \delta{\dot{t}}_k δt˙k

多普勒频移误差对 p b t k w \textbf{p}^w_{b_{t_k}} pbtkw的导数
根据链式求导法则:

第二项比较简单:

第一项比较复杂,但也不涉及很复杂的公式,就是链式求导流程长了点,建议直接用Matlab或者SymPy求导,这里直接给出结论:

其中:

g. Receiver Clock观测
在 t k − 1 t_{k-1} tk−1和 t k t_k tk接收机时钟钟差的变化为

离散化之后:

h.高精RTK定位(载波相位观测)
前面都是单点定位,属于非差观测,是绝对定位。
如果是高精定位,那么需要使用前文提到的双差观测,这里属于相对定位(相对于参考站的位置),下述公式是双差观测方程

类似正常求导即可。此时融合结果可以达到RTK定位精度
i.初始化
参考GVINS的初始化流程,其实也和松耦合类似,分为三步:
i.实验效果
- 融合原始多普勒平移测量比直接松耦合融合接收机解算的GPS速度的精度更高一些
- 融合伪距测量相当于融合单点GPS位置,融合后局部位置精度可能会下降,但是相比不融合的全局位置精度会提高,相对松耦合来说,由于融合了原始测量,因此效果会比直接融合解算的位置要好。在卫星数小于4颗时,接收机无法求解出GPS位置和速度,但紧耦合不受影响,卫星少也能融合。
- 融合载波相位也是同样的道理,就相当于松耦合融合接收机解算的RTK位置了


