R:应用时间序列分析--基于R(2)第二章 时间序列的预处理
第二章 时间序列的预处理
-
- 2.1平稳序列的定义
-
- 2.1.1特征统计量
- 2.1.2 平稳时间序列的定义
-
- 严平稳
- 宽平稳
- 2.1.3 平稳时间序列的统计特征
- 2.1.4 平稳时间序列的意义
- 2.2 平稳性检验***
-
- 2.2.1 时序图检验
- 自相关图检验
- 2.3 纯随机性检验***
-
- 2.3.1 纯随机序列定义
- 2.3.2 纯随机序列的性质
-
- 纯随机性
- 方差齐性
- 2.3.3 纯随机性检验****
-
- 运用假设检验的方式对序列的纯随机性进行检验
-
- 假设条件
- 检验统计量
2.1平稳序列的定义
2.1.1特征统计量
概率分布
特征统计量
2.1.2 平稳时间序列的定义
严平稳
宽平稳
2.1.3 平稳时间序列的统计特征
2.1.4 平稳时间序列的意义
2.2 平稳性检验***
2.2.1 时序图检验
##导入数据(以后最好导入CSV格式数据)
dat1<-read.csv("F:/应用时间序列分析/时间序列分析——基于R(第2版)案例数据/A1_4.csv")
percent<-ts(dat1$percent,start=1978)
plot(percent)
dat2<-read.csv("F:/应用时间序列分析/时间序列分析——基于R(第2版)案例数据/A1_5.csv")
rain<-ts(dat2$rain,start = c(1970,1),frequency = 12)
plot(rain)
dat3<-read.csv("F:/应用时间序列分析/时间序列分析——基于R(第2版)案例数据/A1_6.csv")
Suicide<-ts(dat3$Suicide,start = 1915)
plot(Suicide)
自相关图检验
运用函数acf
acf(x , lag.max= , plot= )
- x : 变量名
- lag.max = : 延迟阶数。 若用户缺省这个参数,系统会根据序列的长度自动指定延迟阶数。
- plot = : 输出自相关图还是自相关系数
(1)系统默认参数是 plot=True ,即只输出自相关图,不输出自相关系数。
(2)若指定是 plot = False , 则只输出自相关系数,不输出自相关图。
(3)获取自相关图之后,可以用 acf(x)$acf 查看自相关系数
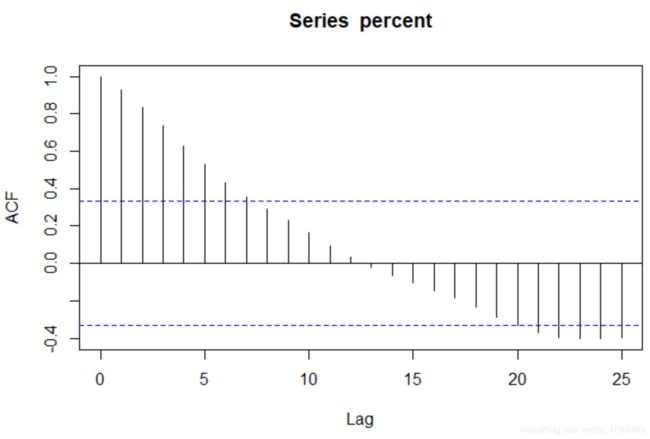
acf(percent , lag.max = 25)
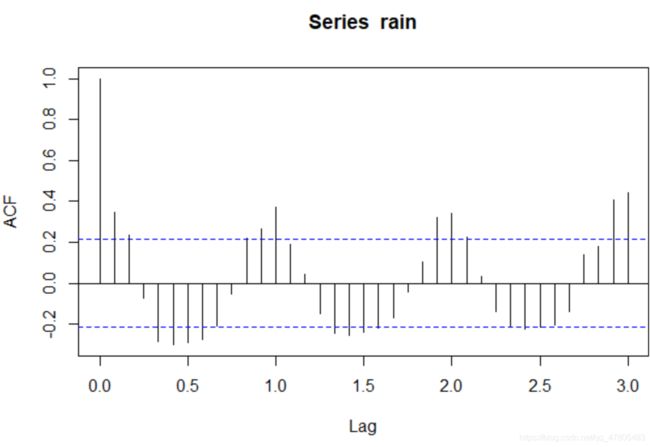
acf(rain,lag.max = 36)
2.3 纯随机性检验***
2.3.1 纯随机序列定义
正态分布随机数生成函数是 rnorm 。
rnorm(n = , mean = , sd = )
###产生1000个服从标准正态分布的随机数构成的一个白噪声序列
white_noise<-rnorm(1000)
white_noise<-ts(white_noise)
plot(white_noise)
2.3.2 纯随机序列的性质
纯随机性
方差齐性
2.3.3 纯随机性检验****
###产生1000个服从标准正态分布的随机数构成的一个白噪声序列
white_noise<-rnorm(1000)
white_noise<-ts(white_noise)
plot(white_noise)
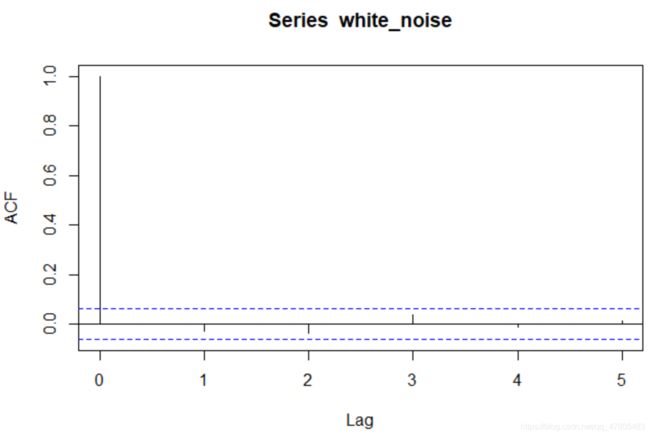
###绘制白噪声序列的样本自相关图
acf(white_noise)
acf(white_noise,lag.max = 5)$acf
运用假设检验的方式对序列的纯随机性进行检验
假设条件
原假设:延迟期数小于等于m期的序列值之间相互独立。
备择假设:延迟期数小于等于m期的序列值之间具有相关性
检验统计量
Q统计量
LB统计量
运用 Box.test 函数进行序列的纯随机性检验
Box.test (x , type = , lag= )
- x : 变量名
- type : 检验统计量类型
(1)type = "Box-Pierce " Q统计量
(2)type = “Ljung-Box” LB统计量
# 录入数据
x <- c(10,15,10,10,12,10,7,7,10,14,
8,17,14,18,3,9,11,10,6,12,
14,10,25,29,33,33,12,19,16,19,
19,12,34,15,36,29,26,21,17,19,
13,20,24,12,6,14,6,12,9,11,
17,12,8,14,14,12,5,8,10,3,
16,8,8,7,12,6,10,8,10,5)
x <- ts(x)
# 绘制时序图
plot(x)
# 绘制自相关图,延迟20阶
acf(x,lag.max = 20,main="lag.max = 20")
# 纯随机性检验,延迟10阶
Box.test(x,type = "Box-Pierce",lag = 10)
Box.test(x,type = "Ljung-Box",lag = 10)
y <- diff(x)
# 绘制时序图
plot(y)
# 绘制自相关图,延迟20阶
acf(y,lag.max = 20,main="lag.max = 20")
# 纯随机性检验,延迟10阶
Box.test(y,type = "Box-Pierce",lag = 10)
Box.test(y,type = "Ljung-Box",lag = 10)
# P46/1
x<-c(1:20)
x<-ts(x)
##第一问
plot(x,type='o')
##第二问
acf(x,lag.max = 6 , main='lag.max = 6')
acf(x)$acf
##第三问
acf(x,lag.max = 20 , main='lag.max = 20')
acf(x)$acf
##P47/4
# 输入12个样本自相关系数
rho <- c(0.02,0.05,0.1,-0.02,0.05,0.01,0.12,-0.06,0.08,-0.05,0.02,-0.05)
# 样本量为100
n = 100
# 计算Q统计量
Q <- n*sum(rho**2)
qchisq(0.95,12)
# Q=4.57明显小于临界值chisq(12)=21.03,所以无法拒绝原假设,认为改序列为纯随机序列。
# 计算LB统计量
k <- c(1:12)
mr = rho**2/(n-k)
LB <- n*(n+2)*sum(mr)
qchisq(0.95,12)
# Q=4.57明显小于临界值chisq(12)=21.03,所以无法拒绝原假设,认为改序列为纯随机序列。
#P48/6
##第一问
# 录入数据
x <- c(10,15,10,10,12,10,7,7,10,14,
8,17,14,18,3,9,11,10,6,12,
14,10,25,29,33,33,12,19,16,19,
19,12,34,15,36,29,26,21,17,19,
13,20,24,12,6,14,6,12,9,11,
17,12,8,14,14,12,5,8,10,3,
16,8,8,7,12,6,10,8,10,5)
x <- ts(x)
# 绘制时序图
plot(x)
# 绘制自相关图,延迟20阶
acf(x,lag.max = 20,main="lag.max = 20")
# 纯随机性检验,延迟10阶
Box.test(x,type = "Box-Pierce",lag = 10)
Box.test(x,type = "Ljung-Box",lag = 10)
##第二问
y <- diff(x)
# 绘制时序图
plot(y)
# 绘制自相关图,延迟20阶
acf(y,lag.max = 20,main="lag.max = 20")
# 纯随机性检验,延迟10阶
Box.test(y,type = "Box-Pierce",lag = 10)
Box.test(y,type = "Ljung-Box",lag = 10)