微分几何笔记(4) —— 二维三维空间中曲线的曲率以及环绕数

本篇文章我们从一般化的 ${\mathbb{R}}^n$ 空间回到我们生活的 ${\mathbb{R}}^2,{\mathbb{R}}^3$空间，看看低维空间中的曲线有哪些性质，主要计算下在非弧长参数下的曲线，曲率挠率的一般表达式。
最后引入环绕数的概念，讲讲怎么数曲线转了多少圈。
 
 

4.1 二维空间中的曲线

二维空间中的曲线(plane curves)的Frenet运动方程：
$$\frac{d}{dt}\left(\begin{array}{c}{e}_1(t)\\ e_2(t)\end{array}\right)=\left(\begin{array}{cc}0& \omega (t)\\ -\omega (t)& 0\end{array}\right)\cdot \left(\begin{array}{c}{e}_1(t)\\ e_2(t)\end{array}\right)$$
这里 $\omega (t)={\omega }_{1,2}(t)=e_1^{\prime }(t)\cdot e_2(t)$ ，曲率$\kappa (t)\triangleq \frac{\omega (t)}{|c^{\prime }(t)|}$，详细的定义写在之前一篇笔记中。
进一步，在弧长参数下有$c^{\prime \prime }(s)=e_1^{\prime }(s)=\omega (s)e_2(s)=\kappa (s)e_2(s)$ 所以有 $|c^{\prime \prime }(s)|=|\kappa (s)|$

这里我们可以看到平面曲线曲率正负的意义：
首先最主要的一点是，因为在每一点曲率是一个数而已，这说明曲线二阶导的方向，与 $e_2(s)$的方向相同或者相反，总之他们在一条直线上！
（我写完之后几天又绕回了这个问题，发现这是相当本质的一个结论，$n$维欧式空间中，非退化的曲线，自身前 $n$ 阶导数就是正交的！）

因为二阶导数的正负，决定了曲线的凹凸性，二阶导大于0，曲线下凸；二阶导小于0，曲线上凸；二阶导等于0，曲线没有凸性。
再结合由Frenet标架自身性质所决定的，$e_1(s)$为曲线的切线方向，$e_2(s)$由$e_1(s)$逆时针旋转 $90^{\circ }$ 得到（为了和${\mathbb{R}}^2$空间中的基底保持相同定向。）所以我们知道，$\kappa (s)>0$ 表示$e_2(s)$与曲线弯曲方向相同，反之，则相反；若$\kappa (s)=0$自然表示曲线在这一点处不弯曲。（不同的参数 $s$ 或者 $t$ 并不改变上述向量的方向，只是在大小上相差个常数倍。）

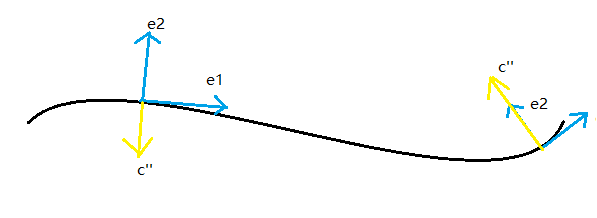
接下来，我们来算一算，如果不对曲线进行弧长参数化，用最原本的参数，曲率的表达式是怎样的：

Proposition 4.1.1   $c:I\to {\mathbb{R}}^2$ 为一条满足Frenet条件的参数化平面曲线，则其曲率 $\kappa (t)=\frac{\text{det}(c^{\prime }(t),c^{\prime \prime }(t))}{|c^{\prime }(t){|}^3}$

Proof:
对任意参数曲线，都可以写成$c=\tilde{c}\circ \varphi$的形式，这里 $s=\varphi (t)={\int }_{x_0}^t|c^{\prime }(\tau )|d\tau ,\therefore {\varphi }^{\prime }=|c^{\prime }(t)|$（证明写在笔记(2)中的命题2.2.5）
那么
$c^{\prime }(t)={\varphi }^{\prime }({\tilde{c}}^{\prime }\circ \varphi ),c^{\prime \prime }(t)={\varphi }^{\prime \prime }({\tilde{c}}^{\prime }\circ \varphi )+({\varphi }^{\prime }{)}^2({\tilde{c}}^{\prime \prime }\circ \varphi )$
注意这里${\tilde{c}}^{\prime }\circ \varphi ={\tilde{c}}^{\prime }(s)={\tilde{e}}_1,{\tilde{c}}^{\prime \prime }\circ \varphi ={\tilde{c}}^{\prime \prime }(s)=\tilde{\kappa }(s){\tilde{e}}_2(s)$
写成矩阵的形式：
$$\left(\begin{array}{c}{c}^{\prime }(t)\\ c^{\prime \prime }(t)\end{array}\right)=\left(\begin{array}{cc}{\varphi }^{\prime }& 0\\ {\varphi }^{\prime \prime }& {\varphi }^{{}^{\prime }2}\end{array}\right)\left(\begin{array}{cc}1& 0\\ 0& \tilde{\kappa }\end{array}\right)\left(\begin{array}{c}{\tilde{e}}_1(t)\\ {\tilde{e}}_2(t)\end{array}\right)$$由于曲率在参数变换下不变，上式两边取行列式便得到了结果。

事实上，曲线为平面圆周，当且仅当曲率恒为非零常数；当曲率恒为零时，对应的曲线退化为一条直线。

4.2 三维空间中的曲线

类似的，我们可以计算一般非弧长参数曲线的曲率。在三维空间中，“曲率”含有两部分，曲率$\kappa (t)$ 和挠率 $\tau (t)$，分别计算下：
Proposition 4.2.1   $c:I\to {\mathbb{R}}^3$ 为一条满足Frenet条件的参数化空间曲线，则其曲率 $\kappa (t)=\frac{|c^{\prime }(t)\times c^{\prime \prime }(t)|}{|c^{\prime }(t){|}^3}$, $\tau (t)=\frac{\text{det}(c^{\prime }(t),c^{\prime \prime }(t),c^{\prime \prime \prime }(t))}{|c^{\prime }(t)\times c^{\prime \prime }(t){|}^2}$.

Proof:
与二维情况类似，将曲线写为 $c=\tilde{c}\circ \varphi$，然后求导，写成矩阵形式：
$$\left(\begin{array}{c}{c}^{\prime }(t)\\ c^{\prime \prime }(t)\\ c^{\prime \prime \prime }(t)\end{array}\right)=\left(\begin{array}{ccc}{\varphi }^{\prime }& & \\ {\varphi }^{\prime \prime }& {\varphi }^{{}^{\prime }2}& \\ {\varphi }^{\prime \prime \prime }& 3{\varphi }^{\prime }{\varphi }^{\prime \prime }& ({\varphi }^{\prime }{)}^3\end{array}\right)\left(\begin{array}{ccc}1& & \\ 0& \tilde{\kappa }(s)& \\ -{\tilde{\kappa }}^2(s)& {\tilde{\kappa }}^{\prime }(s)& \tilde{\kappa }(s)\tilde{\tau }(s)\end{array}\right)\left(\begin{array}{c}{\tilde{e}}_1(t)\\ {\tilde{e}}_2(t)\\ {\tilde{e}}_3(t)\end{array}\right)$$

先计算曲率$\kappa (t)$：$c^{\prime }(t)\times c^{\prime \prime }(t)={\varphi }^{\prime }(t){\tilde{e}}_1(s)\times ({\varphi }^{\prime \prime }{\tilde{e}}_1(s)+({\varphi }^{\prime }{)}^2\tilde{\kappa }(s){\tilde{e}}_2(s))=|c^{\prime }(t){|}^3\tilde{k}(s){\tilde{e}}_3(s)$

由曲率的参数变换不变性，$\kappa (t)=\frac{|c^{\prime }(t)\times c^{\prime \prime }(t)|}{|c^{\prime }(t){|}^3}$.

再在上面矩阵两边取行列式，就得到：$\tau (t)=\frac{\text{det}(c^{\prime }(t),c^{\prime \prime }(t),c^{\prime \prime \prime }(t))}{|c^{\prime }(t)\times c^{\prime \prime }(t){|}^2}$
 
 

空间曲线由曲率和挠率唯一决定，假若二者均为常数（注意在空间中，曲率$\kappa >0$）：
1.当$\tau \ne 0$时，曲线为螺旋线(Helix)；
2.当$\tau$恒为非零常数时，曲线退化为平面圆周。

证明也很简单，一方面螺旋线的曲率挠率恒为常数；另一方面，任意恒为常数的曲率挠率，总可以写成螺旋线所对应的形式。

接下来我们再来看一看Frenet标架，是如何唯一决定曲线的.
我们试图对一条弧长参数化曲线进行泰勒展开来做，这就涉及到用Frenet标架来表示曲线的导数，这个也好办，上方矩阵形式的最后两个矩阵就是我们要的：
$$\left(\begin{array}{c}{c}^{\prime }(s)\\ c^{\prime \prime }(s)\\ c^{\prime \prime \prime }(s)\end{array}\right)=\left(\begin{array}{ccc}1& & \\ 0& \kappa (s)& \\ -{\kappa }^2(s)& {\kappa }^{\prime }(s)& \kappa (s)\tau (s)\end{array}\right)\left(\begin{array}{c}{e}_1(s)\\ e_2(s)\\ e_3(s)\end{array}\right)$$

我们现在可以用泰勒公式了：
$\begin{array}{rl}c(s_0+s)& \approx c(s_0)+s{c}^{\prime }(s_0)+\frac{s^2}{2}{c}^{\prime \prime }(s_0)+\frac{s^3}{6}{c}^{\prime \prime \prime }(s_0)\\ & =c(s_0)+(s-\frac{{\kappa }^2}{6}{s}^3)e_1+(\frac{\kappa }{2}{s}^2+\frac{{\kappa }^{\prime }}{6}{s}^3)e_2+\frac{\kappa \tau }{6}{s}^3{e}_3\end{array}$

因为 $s$ 是小量，其高阶可以扔掉，所以在 $e_1-e_2$ 平面上，曲线的改变近似为$(s,\frac{\kappa }{2}{s}^2)$;
在 $e_1-e_3$ 平面上，曲线的改变近似为$(s,\frac{\kappa \tau }{6}{s}^3)$;
在 $e_2-e_3$ 平面上，曲线的改变近似为$(\frac{\kappa }{2}{s}^2,\frac{\kappa \tau }{6}{s}^3)$.

这里刚好说到第三个曲线，被成为Neil抛物线，其特点是在尖点(cusp)处连续可导，当然在这里他就不满足函数的定义了。

将他们画在三维坐标系中：

（图来自 UTM Calculus and Analysis in Euclidean Space p402）
这里$T$是Tangent vector的简写，对应$e_1$;
$N$ 是Normal vector，对应$e_2$;
$B$ 是Binormal vector，对应$e_3$.
 
 

4.3 环绕数定理

这个是平面曲线的全局性质(Global Theory)，之前讲的标架，曲率都是对曲线的局部而言，那么对全局我们可以先考虑，比方说，曲线转了多少圈。
这一章在Klingenberg的书中语言叙述还是挺繁琐的，直观理解就好。

先说下什么是闭曲线：
用好理解的说法，这条曲线具有周期性，且处处都是光滑的(特别是在相同两部分连接的地方)。在傅里叶分析里我们还会见到他，圆上的曲线。
简单就是一一映射的意思。
所以简单闭曲线就是一条光滑周期参数曲线，且在每个周期上，都是一一映射的。

接下来是环绕数的概念：
在平面上一个光滑参数曲线的切向量是会随着曲线的方向转的，取定一个固定的坐标系，把切向量和 $x$-坐标轴的夹角定义为$\theta (t)$ ，其中 $t$ 为曲线的参数，那么显然这个 $\theta (t)$ 除了在 $\pi$ 和 $2\pi$ 这两个零界点附近都是光滑的。

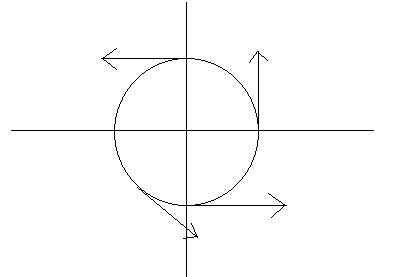
拿圆举例子，在起始位置，它的切向量和x轴夹角为$\frac{\pi }{2}$，继续逆时针前进，到它的正上方时，夹角为$\pi$，快到正下方，却还没到时，夹角接近 $2\pi$ ，当到了正下方后，与$x$-轴夹角从新从0算起。
所以我们总可以通过给夹角加一个$2\pi$的整数倍，使得这个夹角函数$\theta (t)$是连续且可导的，比方说刚说的例子，本来过了圆周的正下方，夹角重新回到0，我们只要对他加$2\pi$，使得夹角变成 $2\pi +\theta$，变成全局的连续可导函数即可。

环绕数，对光滑参数曲线，定义为在曲线的两个端点$[a,b]$的角度之差再除$2\pi$：$$n_c=\frac{\theta (b)-\theta (a)}{2\pi }$$.
比方说对单位圆周$c=(\cos \theta ,\sin \theta ),\theta \in [0,2\pi ]$的环绕数，按定义为1；
单位圆周$c=(\cos 2\theta ,\sin 2\theta ),\theta \in [0,2\pi ]$的环绕数，按定义为2；
单位圆周$c=(\cos (-\theta ),\sin (-\theta )),\theta \in [0,2\pi ]$的环绕数，按定义为-1.

更进一步，对于分段光滑的参数曲线，定义一个外角(exterior angle)，记为${\alpha }_i$，表示对于一个分段光滑节点 $a_i$ 左右两端点角度的差值：即从$c^{\prime }(a_i^{-})$到$c^{\prime }(a_i^{+})$的角度差值，规定逆时针为正，顺时针为负，$-\pi <{\alpha }_i<\pi$.
所以对分段光滑参数曲线的环绕数就定义为：$$n_c=\frac{1}{2\pi }\sum _i({\theta }_i(b_i)-{\theta }_i(a_i))+\frac{1}{2\pi }\sum _i{\alpha }_i.$$
这里的$a_i,b_i$表示分段光滑区间的端点。
 
 

接下来是看起来很显然，但很有用的环绕数定理(Umlaufsatz)，这是他的德语名字。
Theorem 4.3.1 假设$c:I\to {\mathbb{R}}^n$是一条分段光滑的，正则的简单闭曲线，则它的环绕数$n_c=\pm 1.$
 
 

这里的简单闭曲线其实可以很复杂：
比如简单光滑曲线可以不简单：

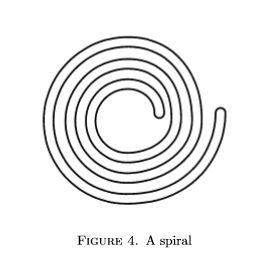
再比如简单分断光滑曲线可以相当复杂：

但他们的环绕数其实都是$1$或者$-1$，即绕着走到起点，其实都只绕了一圈。

 
 

参考：
[1]W. Klingenberg.   A course in differential geometry.   Translated from the German by David Hoffman. Graduate Texts in Mathematics, Vol. 51. Springer-Verlag, 1978.
[2]J. Shurman.   Calculus and Analysis in Euclidean Space   Undergraduate Texts in Mathematics,Springer-Verlag, 2016.
[3]厦门大学杨波老师的讲义：http://math.xmu.edu.cn/group/ga/dg_files/surface_notes.pdf