Toponogov 比较定理及其应用
1. Toponogov 比较定理的背景来源
Victor Andreevich Toponogov(1930-2004) 是苏联数学家,Toponogov 比较定理是他的博士论文题目,在1958年答辩。他证明这个定理是为了用于证明截面曲率假设下的分裂定理和最大直径定理,这两个定理后来都被推广到了只需要里奇曲率的假设。Berger 首先在证明 1 4 \frac{1}{4} 41-pinched sphere theorem 中用到了 Toponogov 比较定理,后来和 Grove Shiohama 的 Critical point theorem 被 Gromov 一起用来估计非负截面曲率流形的 Betti 数的估计。
2. 定理叙述及其几何理解
以下内容,我主要参考教材: Cheeger & Ebin 的 Comparison Theorems in Riemannian Geometry 以及上课的笔记。
首先我们定义测地三角形,这是欧氏空间里三角形的推广:
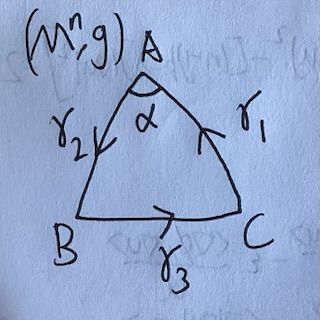
定义2.1 (测地三角形)黎曼流形 M n M^n Mn 上的一个测地三角形,是一个集合,它由三个顶点 A , B , C A, B, C A,B,C 和三条分别连接两个不同顶点、首尾相接、具有单位速度的最短测地线段构成,用 Δ A B C \Delta ABC ΔABC 表示。
三角形各顶点各边的记号如下图所示:
注意这里定义,教材中要求两边之和大于第三边,而不要求最短测地线;有的教科书则直接要求最短测地线,比如 Petersen 的黎曼几何,其后面注释也有提到,其实证明中只要求在空间形式上对应的测地线是最短的。如 Petersen 上面的证明,这个定理也可以从方程的角度,比如用所谓的 R i c c a t i Riccati Riccati 比较来证明。
三角形去掉一边,定义为铰链(Hinge):
定义2.2 (铰链)由流形上一点 A A A 和两条最短测地线 γ 1 , γ 2 \gamma_1, \gamma_2 γ1,γ2 构成, γ 1 ( l 1 ) = γ 2 ( 0 ) = A \gamma_1(l_1)=\gamma_2(0)=A γ1(l1)=γ2(0)=A,角度记为 α \alpha α. 用 ( A , γ 1 , γ 2 ) (A, \gamma_1, \gamma_2) (A,γ1,γ2) 表示。

铰链就长这样↑
定理2.3 (Toponogov) ( M n , g ) (M^n, g) (Mn,g) 是一个完备黎曼流形,其截面曲率 K M ≥ H , H K_M\geq H, H KM≥H,H 是某个固定常数, M ‾ \underline{M} M 是二维常截面曲率 H H H 的空间形式,则:
(i)(三角形比较) ∀ Δ A B C ⊂ M , ∃ \forall \Delta ABC\subset M, \exist ∀ΔABC⊂M,∃ 比较三角形 Δ A B C ‾ ⊂ M ‾ \Delta \underline{ABC}\subset \underline{M} ΔABC⊂M, 使得二者边长对应相等,角度满足:
α ‾ ≤ α , β ‾ ≤ β , γ ‾ ≤ γ . \underline{\alpha}\leq\alpha, \underline{\beta}\leq\beta, \underline{\gamma}\leq\gamma. α≤α,β≤β,γ≤γ.并且比较三角形在合同变换的意义下唯一(除了 H > 0 H>0 H>0,且存在一条边的长度等于空间形式的直径时);
(ii)(铰链比较) ∀ ( A , γ 1 , γ 2 ) ⊂ M , ∃ \forall (A, \gamma_1, \gamma_2)\subset M, \exist ∀(A,γ1,γ2)⊂M,∃ 比较铰链 ( A ‾ , γ 1 ‾ , γ 2 ‾ ) ⊂ M ‾ (\underline{A}, \underline{\gamma_1}, \underline{\gamma_2})\subset\underline{M} (A,γ1,γ2)⊂M,使得 d ( γ 1 ( 0 ) , γ 2 ( l 2 ) ) ≤ d ‾ ( γ 1 ‾ ( 0 ) , γ 2 ‾ ( l 2 ) ) . d(\gamma_1(0), \gamma_2(l_2))\leq\underline{d}(\underline{\gamma_1}(0), \underline{\gamma_2}(l_2)). d(γ1(0),γ2(l2))≤d(γ1(0),γ2(l2)).
定理2.3的(i)说明较大曲率流形上的三角形,和二维空间形式上的三角形相比,边长相等时,曲率大则角度也大。比方说我们比较球面和欧氏空间上的三角形,由高斯博内公式可知,球面上三角形的内角和大于 π \pi π;比较欧氏空间和双曲空间,同样可知双曲空间上三角形的内角和小于 π \pi π,这也符合Toponogov比较定理。直观上来看,球面上的三角形更“胖”,双曲空间上的三角形更“瘦”。更近一步,Toponogov比较定理说大曲率流形上三角形的每个角都更大。
3. 证明概叙
首先我们考虑曲率为 H − ϵ H-\epsilon H−ϵ 的空间形式,原因在我的理解里有两个:
其一是此时排除了一条边长度等于球面经线长度的情况,使得比较三角形在合同的意义下唯一;
其二是在证明(5)(6)(7)步中,要对瘦的(Thin)铰链证明时,需要保证沿着一条边,每个点的单射半径有大于零的下界(即书中要求沿着一条边没有 focal point)。
证明分为 10 10 10 步:
(1)对空间形式上的铰链而言,所去除那条边的长度,随铰链的角度 α ‾ \underline{\alpha} α 严格单调递增,并且长度有上下界:
证明可以用第一变分公式(Cheeger&Ebin),对一组测地线变分,变分公式中的积分项为 0 0 0,只剩边界项在一边端点取值;
也可以用空间形式上的余弦定理(Petersen)直接得到。
(2)证明比较三角形在合同变换(Congruence)下的唯一性:
因为空间形式具有齐性,任意两点可以通过空间形式的等距映射对应起来,这样对应了三角形的第一个点,第二个点根据长度相等也被固定,第三个点之间至多相差一个反射。
(3)证明定理叙述(i)中三角形的比较等价于(ii)中铰链的比较:
这一步主要用到单调性,分别画出流形和空间形式上的三角形和铰链,绕两下就可以比较出来。
这样我们接下来的步骤只需要对铰链证明即可。
(4)证明对于小的(Small)铰链,结论(ii)成立:
所谓小的铰链 ( A , γ 1 , γ 2 ) (A, \gamma_1, \gamma_2) (A,γ1,γ2),是指两条边的长度都小于顶点单射半径的一半:
L ( γ i ) < 1 2 inj A , i = 1 , 2. L(\gamma_i)<\frac{1}{2}\text{inj}_A, \quad i=1,2. L(γi)<21injA,i=1,2.这样确保了连成三角形后,第三条边同样在顶点的单射半径里。“小的”三角形也是类似的定义,三角形分别除去一条边得到的三个铰链,都是小的。
这一步是我觉得最有意思的一步,别的步骤是进行转化、剖分、归纳之类的操作,这一步要用到之前所讲的 Rauch 比较定理的第二个版本:
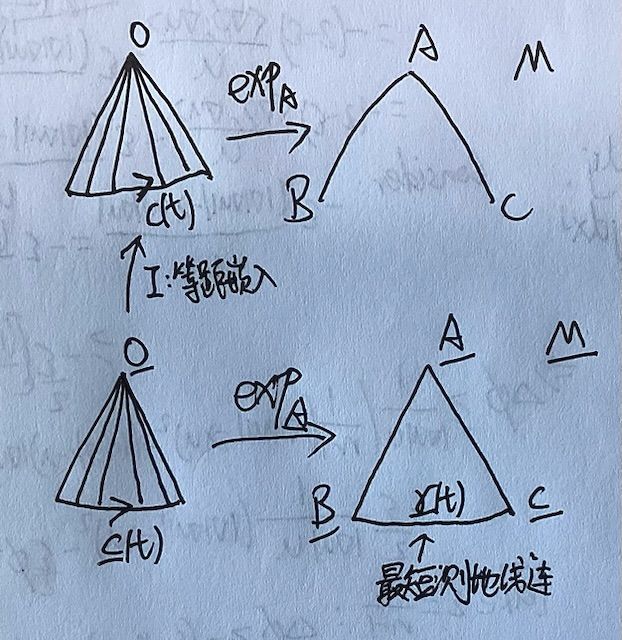
先在空间形式上用最短测地线 γ ‾ ( t ) \underline{\gamma}(t) γ(t)连接铰链,将这条最短测地线通过指数映射拉回到 A ‾ \underline{A} A 的切空间中,得到曲线 c ‾ ( t ) \underline{c}(t) c(t),通过等距嵌入, c ‾ ( t ) \underline{c}(t) c(t)对应到流形上 A A A 点处的切空间里的曲线 c ( t ) c(t) c(t),注意这时 exp A ( c ( t ) ) \text{exp}_A(c(t)) expA(c(t)) 并不一定是连接流形上铰链的测地线;
有了这两条曲线,我们可以得到流形和空间形式上的两族测地线的变分,验证他们满足 Rauch 比较定理的条件,可以得到他们在端点处的变分向量场的比较,从而得到曲线长度的比较 L ( γ ‾ ) ≥ L ( γ ) L(\underline{\gamma})\geq L(\gamma) L(γ)≥L(γ),因为 γ \gamma γ 并不一定是最短测地线,所以有结论成立。
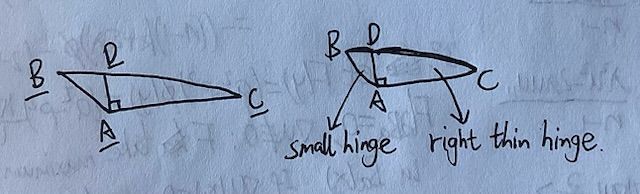
(5)证明对瘦的(Thin)直角铰链(ii)成立:
空间形式中的铰链用最短测地线连接斜边,再像第(4)步一样,瞄准 Rauch 比较定理的条件,构造垂直一边的平行单位向量场,然后写出变分,照搬到原先的流形 M M M 上,这时流形上连接铰链的曲线由空间形式上搬过来,不一定是最短测地线。
所谓瘦的直角铰链,就是指对流形中的图形,选定的那条边没有 focal point(有点拗口),看下方图形很直观可以理解。
这样就可以应用 Rauch 比较定理得出结论。
(6)证明对瘦的钝角铰链(ii)成立:
从空间形式出发,将用最短测地线连接的铰链剖分成直角三角形和一个新的钝角三角形,对钝角铰链而言,“瘦”是指剖分后,得到一个瘦的直角三角形和一个“小”的三角形。
(7)证明对瘦的锐角铰链(ii)成立:
如下图,瘦的锐角铰链是指,用最短测地线连接后,从一个铰链的“脚”向内做垂线,会得到一个小的三角形和一个瘦的直角三角形。
我们先比较小三角形,再比较剩余部分就可以得到结论。
(8)(9)证明对一般铰链(ii)成立:
将一般的三角形剖分成充分瘦的三角形,再用归纳法。
(10)令 ϵ → 0 \epsilon\rightarrow0 ϵ→0即可。
4. Toponogov 比较定理的应用
4.1 Petersen书中的介绍
这里只能粗略的介绍,Petersen 的黎曼几何(第三版)第12章介绍了很多应用,第12章的前言总结的很好,摘录在这里:
It wasn’t until Grove and Shiohama developed critical point theory to prove their diameter sphere theorem that Toponogov’s theorem was put to serious use. Shortly after that, Gromov put these two ideas to even more nontrivial use, with his Betti number estimate for manifolds with nonnegative sectional curvature. After that, it became clear that in working with manifolds that have lower sectional curvature bounds, the two key techniques are Toponogov’s theorem and the critical point theory of Grove-Shiohama.
正文中的内容这里只取前两个:
1. 1. 1. Rauch-Berger-Klingenberg sphere theorem, 或者 1 4 \frac{1}{4} 41-pinched sphere theorem.
定理4.1.1( 1 4 \frac{1}{4} 41-Pinched Shpere Theorem)对于一个单连通闭的黎曼流形 ( M n , g ) (M^n,g) (Mn,g),如果截面曲率满足 s e c M ∈ ( 1 , 4 ] sec_M\in(1,4] secM∈(1,4],则 M M M 同胚于 S n S^n Sn.
2. 2. 2. Soul Theorem.
定理4.1.2 (Soul Theorem)如果完备非紧的黎曼流形 ( M , g ) (M,g) (M,g) 满足截面曲率 s e c M ≥ 0 sec_M\geq0 secM≥0,则 M M M 包含一个灵魂 S S S,它是一个闭的全凸子流形,并且 M M M 微分同胚于底流形为 S S S 的某个法丛。更进一步,如果 M M M 的截面曲率处处为正,则灵魂 S S S 是一个点,因此 M M M 微分同胚于 R n \mathbb{R}^n Rn.
这个定理的证明想法我曾在去年(2022年)戎老师度量黎曼几何的期末口试上讲过。后来 Cheeger 猜想只需要在一点处截面曲率全为正的,就能推出流形的灵魂是一个点,被称为灵魂猜想。这个猜想的证明是佩雷尔曼的“成名作”,证明只有两页。
后续还提及了有限性定理等等,这里就不说了(主要还没学会)。
4.2 Alexandrov空间
如课上所讲,Toponogov 比较定理在 Alexandrov 空间中是类似公理的内容,所谓的 C A T ( k ) CAT(k) CAT(k) 空间,其中 T 就代表着 Toponogov,事实上 Toponogov 和 Alexandrov 两人也互相影响(这块东西我也是一窍不通)。
参考文献:
[1] 课程笔记;
[2] Peter Petersen. Riemannian Geometry, 3rd edn;
[3] Cheeger, Ebin, Comparison Theorems in Riemannian Geometry.
[4] Toponogov 的遗产:http://www.pdmi.ras.ru/EIMI/2020/GL/toponogov.html