Apriori算法通俗讲解

一、Apriori算法简介

       Apriori算法用于解决大规模数据集的关联分析问题。关联分析（association analysis）或关联规则学习（association rule learning）是从大规模数据集中寻找物品间的隐含关系。但是，寻找物品的不同组合是一项十分耗时的任务，计算代价高，蛮力搜索并不能解决问题，所以需要更智能的方法在合理时间范围内找到频繁项集。Apriori算法就是解决这个问题的。

二、关联分析

       关联分析是一种在大规模数据集中寻找有趣关系的任务。这些关系可以有两种形式：（1）频繁项集，（2）关联规则。

（1）频繁项集

频繁项集：是经常出现在一块的物品的集合。

量化方法：支持度（support）。支持度是数据集中包含该项集的记录所占的比例。例如数据集[[1, 3, 4], [2, 3, 5], [1, 2, 3], [2, 5]]中，项集{2}的支持度为3/4，项集{2,3}的支持度为1/2。

（2）关联规则

关联规则：暗示两种物品之间可能存在很强的关系。

量化计算：可信度或置信度（confidence）。可信度是针对一条关联规则（如{2}-->{3}）来定义的。{2}-->{3}这条规则的可信度为“支持度{2，3}/支持度{2}”，即2/3，意味着包含{2}的所有记录中2/3符合规则包含{2,3}。

三、Apriori原理

       无论频繁项集还是关联规则都需要计算支持度。如果数据量小，计算一个项集的支持度可以针对每个项集扫描所有数据，然后统计该项集出现的总数除以总的交易记录数，就可以得到支持度。但是对于N个物品的数据集共有2N-1中项集组合，即使4个物品也需要遍历数据集15次，100种物品有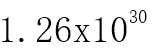中可能的项集组合，对现代计算机而言，需要很长的时间才能完成运算，何况事实上，商店都会有上百上千种商品。

       Apriori算法可以降低计算时间，减少可能感兴趣的项集。

       Apriori原理：如果某个项集是频繁的，那么它的所有子集也是频繁的。如若{2,3}是频繁的，那么{0}、{1}也一定是频繁的。反过来同样，如果一个项集是非频繁集，那么它的所有超集也是非频繁的。如若{2,3}是非频繁的，那么{0,2,3}、{1,2,3}、{0,1,2,3}也是非频繁项。所以如果计算出{2,3}的支持度是非频繁的，那么{0,2,3}、{1,2,3}、{0,1,2,3}的支持度就不用计算了。

Apriori原理可以避免项集数目的指数增长，从而在合理时间内计算出频繁项集。

四、Apriori算法发现频繁项集

Apriori算法流程：

1）首先，基于数据集生成个数为1的项集的列表C1；

2）根据频繁项集函数，计算C1中各元素的支持度，去掉不满足最小支持度的元素，生成满足最小支持度的频繁项集列表L1；

3）根据创建候选项集函数，基于L1生成k=2的候选项集列表C2；

4）根据频繁项集函数，基于C2生成满足最小支持度的k=2的频繁项集列表L2；

5）增加k的值，重复3）、4）生成Lk，直到Lk为空时，返回L列表，L包含L1、L2、L3...

       以下是创建候选项集函数及解释。

       至于为什么是比较前k-2个元素呢，一般初始项集个数为1，由k=1的项集生成k=2的项集。所以k的初始值也为2。如果要生成个数为k的项集，则比较前k-2项，如果相等合并，正好比较的项各剩下1个不相等的元素，这样合并后个数就为k-2+1+1=k项。（以下是举例推导过程，忽略C2经过滤后生成L2，直接将C2视为L2，相当于支持度为0）

       比较前k-2个元素，可以减少遍历列表的次数。比如想利用{0,1}、{0,2}、{1,2}来创建三元素项集，如果将每两个集合合并，就会得到{0,1,2}、{0,1,2}、{0,1,2}。同样的结果结合会重复3次，还需要处理以得到非重复结果。现在只比较第k-2=1个元素，第1个元素相同才合并集合，得到{0,1,2}，只有一次操作，这样就不需要遍历列表来寻找非重复值。

五、从频繁项集中挖掘关联规则

       首先从一个频繁项集开始，接着创建一个规则列表，其中规则右部只包含一个元素，然后对这些规则进行测试。接下来合并所有剩余规则来创建一个新的规则列表，其中规则右部包含两个元素。这种方法也被称作分级法。【待续】