Logistic Regression with a Neural Network mindset _吴恩达老师深度学习课后作业

Logistic Regression with a Neural Network mindset

本篇博客主要是个人在完成吴恩达老师第二周的课后作业的实验记录，期间遇到过很多问题和还有个人的一些思考，所以写此博客，以便分享和日后回顾。个人实现过程主要参考了这个up：ladykaka007的教学视频，大家也可以前往一同学习。

1.背景补充

Logistic回归是一种广义线性回归（generalized linear model），是一个常用于二分类(binary classification)的算法（线性回归的模型形式基本上相同，都具有 w‘x+b，其中w和b是待求参数）。吴老师用一个二分类的例子（即识别一张图片是否为猫，是则输出标签 1 作为结果；如果识别出不是猫，那么输出标签 0 作为结果），向我们说明了神经网络的基础知识。

2.实验过程

2.1实验环境

在实验的过程中，实用的开发工具为jupyter notebook，接着提前安装好实验需要的库，如下所示：

• numpy（科学计算相关）
• h5py(这个是用来处理数据集的库）
• matplotlib（图像相关）
• PIL（这个库安装的时候找不到，好像是Python2的库，我们可以选择安装Pillow库）

2.2数据处理

我们需要将实验中的训练数据和测试数据从本地文件中读入，在这个过程中我们需要注意的是window环境下的文件路径是“\\”！

# 导入数据集
import h5py

# 训练原始数据  注意Windows环境下面的目录要使用双斜杠
train_data = h5py.File('C:\\Users\\佳雨初林\\Desktop\\研究生学习\\吴恩达深度学习作业\\01.机器学习和神经网络\\2.第二周 神经网络基础\\编程作业\\datasets\\train_catvnoncat.h5','r')
# 测试原始数据
test_data = h5py.File('C:\\Users\\佳雨初林\\Desktop\\研究生学习\\吴恩达深度学习作业\\01.机器学习和神经网络\\2.第二周 神经网络基础\\编程作业\\datasets\\test_catvnoncat.h5','r')

.h5文件中的数据是以key：value键值对的形式存在的，所以我们可以查看一下数据的key值：

#查看一下数据集里面的key有哪些（h5文件中的数据是以key：value的形式存储的）
for key in train_data.keys():
    print(key)

可以知道数据的key值有：

key	value
list_classes	图片类别：cat or non-cat
train_set_x	图片的特征值(RGB值）
train_set_y	图片的分类（{0，1})

将这些数据集的维度打印出来看看：

print("train_set_x shape is:",train_data['train_set_x'].shape) #train_set_x shape is: (209, 64, 64, 3)
print("train_set_y shape is:",train_data['train_set_y'].shape #train_set_y shape is: (209,)
print("test_set_x shape is:",test_data['test_set_x'].shape)   #test_set_x shape is: (50, 64, 64, 3)
print("test_set_y shape is:",test_data['test_set_y'].shape		 #test_set_y shape is: (50,)

取出原始数据：

# 取出我们的数据集 测试集 (x,y)
train_data_org = train_data['train_set_x'][:]
train_lables_org =train_data['train_set_y'][:]
test_data_org =test_data['test_set_x'][:]
test_lables_org = test_data['test_set_y'][:]

我们可以看一看图片是啥样子的：

# 我们查看一下数据对应的图片
import matplotlib.pyplot as plt
%matplotlib inline
#随机查看第123张图片
plt.imshow(train_data_org[123]) 

接下来我们需要对数据进行处理，这里主要是将单个数据样本向量化，最终也就是将所有的数据集进行矩阵化。向量化、矩阵化的数据是计算机更加擅长处理的，但是在变化的过程中记得多多验证一下数据的维度是否达到了自己的要求，避免在之后的工作内容中出现不必要的错误。

# 记录训练样本和测试样本的个数
m_train = train_data_org.shape[0]   #209
m_test = test_data_org.shape[0]	    #50
print(m_train,m_test)

# 接着我们将元素数据维度进行处理（209，64，64，3）->（209，12288），并转置-》（12288，209）
train_data_tran = train_data_org.reshape(m_train,-1).T
test_data_tran = test_data_org.reshape(m_test,-1).T
# 输出验证一下处理后的数据维度
print("train_data_tran shape is :",train_data_tran.shape)  #train_data_tran shape is : (12288, 209)
print("test_data_tran shape is :",test_data_tran.shape)	 #test_data_tran shape is : (12288, 50)

# 同样也将标签的维度从（209，1）->（209，1）
import numpy as np
train_lables_tran = train_lables_org[np.newaxis,:]
print("train_lables_tran shape is:",train_lables_tran.shape)	#train_lables_tran shape is: (1, 209)
test_lables_tran = test_lables_org[np.newaxis,:]
print("test_lables_tran shape is:",test_lables_tran.shape)	#test_lables_tran shape is: (1, 50)


# 数据的标准化 目的是使特征之间的差值变化不要太大了(将特征同比缩小)
print(test_data_tran)
train_data_sta = train_data_tran / 255
print(train_data_sta)
test_data_sta = test_data_tran / 255

2.3模型搭建

2.3.1 sigmoid函数和参数定义

sigmoid函数是Logistic中常用的激活函数，其函数特性将将任意的输入（-∞，+∞），映射到（0，1）的区间中
这里参数w是每个特征值x对应的权重，参数b则是偏差

# 定义好sigmoid函数
def sigmoid(z):
    a = 1/(1 + np.exp(-z))
    return a
    
# 参数定义
n_dim = train_data_sta.shape[0]
print(n_dim) #12288
w = np.zeros((n_dim, 1))
b = 0    

2.3.2 前向传播

所谓的前向传播，其实就是我们输入数据x到模型中，得到输出y的这个正向过程。但是在这个过程中，我们需要有对这个模型好坏的一个评判标准，这就是损失函数（这是对于单个样本而言的），如果是对于全体训练集的样本来说，就是用代价函数J来评判模型好坏：代价函数J=m个样本的损失函数值之和/m。

# 定义前向传播函数、代价函数以及代价函数对参数求偏导
def propagate(w, b, X, y):
    #1.前向传播函数
    Z = np.dot(w.T, X) + b
    A = sigmoid(Z)
    
    # 2.代价函数
    m = X.shape[1]
    J = -1/m * np.sum(y * np.log(A) + (1-y) * np.log(1-A))
    
    # 3.对于参数求偏导（这里使用了反向传播，起始就是数学中的链式求导
    dw = 1/m * np.dot(X,(A-y).T)
    db = 1/m * np.sum(A - y)
    
    # 定义一个字典
    grands = {'dw':dw , 'db':db}
    
    return grands,J  

2.3.3 参数优化

对于参数w和b的优化选择的是梯度下降算法，在一个连续可导的凸函数（外国的凸函数和国内相反）中，我们可以可以从某一点沿着函数的梯度方向下降，最后可以到达一个global optimism的点，这个点的特征就是代价函数最小，也就是模型有最好表现。这个过程中，参数w和b就是经过多次的迭代（也就是模型训练的过程），最后取得最好的参数w值和参数b值，我们就可以将这两个参数值带入到模型中用来对其他数据进行预测了。
梯度下降法的实现，我们需要完成反向传播的过程，其实就是将代价函数J分别对参数w和b求偏导，这个求偏到的过程涉及到链式准则（就是高数中的链式求导）

# 优化部分
def optimize(w,b,X,y,alpha,n_iters,print_flag):
    # 定义一个空列表，用来存储数据，方便后面画图
    costs = []
    for i in range(n_iters):
        grands,J = propagate(w, b, X, y)
        dw = grands['dw']
        db = grands['db']
        # 我们在上一步中已经求好偏导了，接下来实现梯度下降即可
        w = w - alpha * dw
        b = b - alpha * db
        
        if i % 100 == 0:
            costs.append(J)
            # print_flag是打印的标志位（在下面的实验中可能不需要打印代价函数值）
            if print_flag:
                print('n_iters is :', i,' cost is :', J)
            
    grands = {'dw':dw , 'db':db}  
    params = {'w': w,'b': b}
    
    return grands ,params, costs 

2.3.4 预测函数

我们在优化部分获得参数w和b，接下来就可以实现模型的预测部分了。参数w和b是通过训练集的数据所得出来的，接下来的用于对测试集中的数据进行预测，然后记录好模型输出的结果。

# 预测部分:就是我们使用上面优化好的参数w、b对测试集试进行预测
def predit(w,b,X_test):
    Z = np.dot(w.T, X_test) + b
    A = sigmoid(Z)
    
    m = X_test.shape[1]
    y_pred = np.zeros((1,m))
    
    # 大于0.5认位是猫，取值为1
    for i in range(m):
        if A[:,i] > 0.5:
            y_pred[:,i] = 1
        else:
            y_pred[:,i] = 0
    
    return y_pred

2.3.5 模型整合

模型的整合就是将优化部分和预测部分拼接到一起，这样就获得了逻辑回归模型的完整实现。

# 模型的整合：就是将优化和预测部分整合到一起
def model(w,b,X_train,y_train,X_test,y_test,alpha,n_iters,print_flag):
    grands ,params, costs = optimize(w,b,X_train,y_train,alpha,n_iters,print_flag)
    w = params['w']
    b = params['b']
    
    y_pred_train = predit(w,b,X_train)
    y_pred_test = predit(w,b,X_test)
    
    print("the train acc is :", np.mean(y_pred_train == y_train)*100,'%')
    print("the test acc is :", np.mean(y_pred_test == y_test)*100,'%')
    
    d = {
        'w' : w,
        'b' : b,
        'y_pred_train' : y_pred_train,
        'y_pred_test' : y_pred_test,
        'alpha':alpha,
        'costs':costs
    }
    
    return d

2.4实验结果

接下来调用模型函数，只需要向模型中传入数据就行

# 传入0.005学习率，2000次迭代
d = model(w,b,train_data_sta,train_lables_tran,test_data_sta,test_lables_tran,0.005,2000,True)
# 绘制出训练次数与代价的关系
plt.plot(d['costs'])
plt.xlabel('per hundred iters')
plt.ylabel('cost')

实验结果中（如下），我们不仅对测试集进行了预测，也对训练集经行了预测。 结果很明显，模型对于训练集的预测正确率极高，达到了99%，出现了过拟合；在测试集中的预测结果正确率只有70%，也就是欠拟合的状态。（应该在之后的学习过程中会有优化过程）

3.问题以及思考

3.1学习率的选择

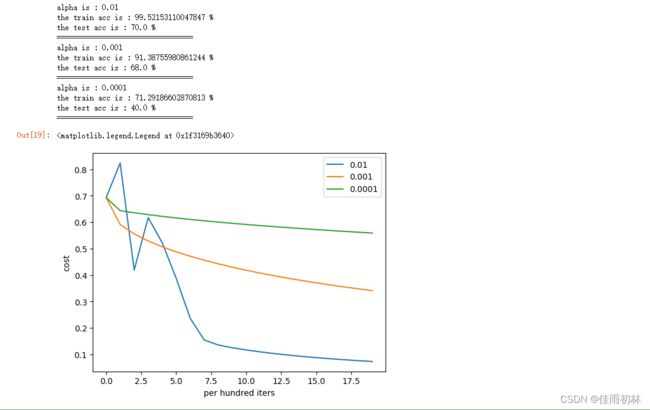
学习率alpha在梯度下降过程中影响下降的幅度，所以用三个不同的学习率来查看其对于代价函数值得影响。

# 比较学习率 alpha对模型的影响
alphas=[0.01, 0.001, 0.0001]
for i in alphas:
    print('alpha is :',i);
    d = model(w,b,train_data_sta,train_lables_tran,test_data_sta,test_lables_tran,alpha=i,n_iters=2000,print_flag=False)
    print('=================================')
    plt.plot(d['costs'],label = str(i))
plt.xlabel('per hundred iters')
plt.ylabel('cost')    
plt.legend()

学习率选择0.01、0.001、0.0001，可以看出学习率的选择也是一个比较重要的因素不可以过小，也不宜偏大。
用0.2的学习率进行实验的时候，模型就出现了问题，出现了报错情况

3.2 本地图片的测试

上传一张本地图片到模型中，看看模型的效果。这个过程中，由于本地图片与数据集中的规格不一致，所以要对本地图片经行相应的处理。

# 用自己电脑本地图片输入到模型中进行预测
local_file_path = 'C:\\Users\\佳雨初林\\Desktop\\猫头.jpg'
local_image = plt.imread(local_file_path )
# 打印出图片看看
plt.imshow(local_image)

# 打印本地图片的尺寸：(200,197,3)
local_image.shape
# 我们需要将图片尺寸改成我们模型中数据集的尺寸：(200,197,3)->(64,64,3)
from skimage import transform
local_image_tran = transform.resize(local_image,(64, 64, 3))
# 将改变尺寸后的图片打印出来看看 
plt.imshow(local_image_tran)

# 最后将改变好尺寸之后的图像数据转化为模型需要的向量数据（12288，1）
local_test = local_image_tran.reshape(64*64*3,1)
local_test.shape
# 直接调用我们的预测函数 这里的参数w，b要传入我们训练好之后的参数
y_test = predit(d['w'],d['b'],local_test)
print(int(y_test))
if (int(y_test)) ==1:
    print('本地输入图片是一只猫')
else:
    print('本地输入图片不是一只猫')

我选的这个图比较奇葩，模型认为我这个图片不是一只猫（哈哈哈，我就是想搞一下这个模型的心态）

4.总结

搭建出了这个逻辑回归模型的过程还是挺有意思的，复习到了很多数学知识，将数学的理论知识实际运用到计算机问题当中，这真的是great！接下来的学习道路还很长，还得脚踏实地，好好加油！