使用 sklearn 进行数学建模的通用模板
前言
无论是本科和研究生都会有的数学建模含金量还是很高的,下面将介绍一下进行数学建模的一些基本操作方法,这里主要是利用sklearn 进行建模,包括前期的一些数据预处理以及一些常用的机器学习模型以及一些简单粗暴的通用建模步骤,仅代表我自己意见。
一、数学建模常见的问题类型
常见的问题类型只有三种:分类、回归、聚类。而明确具体问题对应的类型也很简单。比如,如果你需要通过输入数据得到一个类别变量,那就是分类问题。
分成两类就是二分类问题,分成两类以上就是多分类问题。常见的有:判别一个邮件是否是垃圾邮件、根据图片分辩图片里的是猫还是狗等等。
如果你需要通过输入数据得到一个具体的连续数值,那就是回归问题。比如:预测某个区域的房价等。
常用的分类和回归算法算法有:RF(随机森林)、SVM (支持向量机) 、xgboost、KNN、LR算法、SGD (随机梯度下降算法)、Bayes (贝叶斯估计)以及随机森林等。这些算法大多都既可以解分类问题,又可以解回归问题。
如果你的数据集有对应的属性标签,那我们通常要做的就是对数据划分训练集和验证集,然后再进行预测和评估,选用不同的评价指标来进行评估,比如常见的有accuracy (准确率)、pcc(相关系数)、mse(平均绝对误差)等值。
如果你的数据集并没有对应的属性标签,你要做的,是发掘这组样本在空间的分布, 比如分析哪些样本靠的更近,哪些样本之间离得很远, 这就是属于聚类问题。常用的聚类算法有k-means算法。
二、使用步骤
1.数据集准备工作
在介绍万能模板之前,为了能够更深刻地理解这三个模板,我们加载一个Iris(鸢尾花)数据集来作为应用万能模板的小例子,Iris数据集在前边的文章中已经提到过多次了
代码如下(示例):
from sklearn.datasets import load_iris
data = load_iris()
x = data.data
y = data.target
x值如下,可以看到scikit-learn把数据集经过去除空值处理放在了array里,所以x是一个(150,4)的数组,保存了150个数据的4个特征:
[[5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]
[4.6 3.1 1.5 0.2]
[5. 3.6 1.4 0.2]
[5.4 3.9 1.7 0.4]
[4.6 3.4 1.4 0.3]
[5. 3.4 1.5 0.2]
[4.4 2.9 1.4 0.2]
[4.9 3.1 1.5 0.1]
[5.4 3.7 1.5 0.2]
[4.8 3.4 1.6 0.2]
[4.8 3. 1.4 0.1]
[4.3 3. 1.1 0.1]
[5.8 4. 1.2 0.2]
[5.7 4.4 1.5 0.4]
[5.4 3.9 1.3 0.4]
[5.1 3.5 1.4 0.3]
[5.7 3.8 1.7 0.3]
[5.1 3.8 1.5 0.3]
[5.4 3.4 1.7 0.2]
[5.1 3.7 1.5 0.4]
[4.6 3.6 1. 0.2]
[5.1 3.3 1.7 0.5]
[4.8 3.4 1.9 0.2]
[5. 3. 1.6 0.2]
[5. 3.4 1.6 0.4]
[5.2 3.5 1.5 0.2]
[5.2 3.4 1.4 0.2]
[4.7 3.2 1.6 0.2]
[4.8 3.1 1.6 0.2]
[5.4 3.4 1.5 0.4]
[5.2 4.1 1.5 0.1]
[5.5 4.2 1.4 0.2]
[4.9 3.1 1.5 0.2]
[5. 3.2 1.2 0.2]
[5.5 3.5 1.3 0.2]
[4.9 3.6 1.4 0.1]
[4.4 3. 1.3 0.2]
[5.1 3.4 1.5 0.2]
[5. 3.5 1.3 0.3]
[4.5 2.3 1.3 0.3]
[4.4 3.2 1.3 0.2]
[5. 3.5 1.6 0.6]
[5.1 3.8 1.9 0.4]
[4.8 3. 1.4 0.3]
[5.1 3.8 1.6 0.2]
[4.6 3.2 1.4 0.2]
[5.3 3.7 1.5 0.2]
[5. 3.3 1.4 0.2]
[7. 3.2 4.7 1.4]
[6.4 3.2 4.5 1.5]
[6.9 3.1 4.9 1.5]
[5.5 2.3 4. 1.3]
[6.5 2.8 4.6 1.5]
[5.7 2.8 4.5 1.3]
[6.3 3.3 4.7 1.6]
[4.9 2.4 3.3 1. ]
[6.6 2.9 4.6 1.3]
[5.2 2.7 3.9 1.4]
[5. 2. 3.5 1. ]
[5.9 3. 4.2 1.5]
[6. 2.2 4. 1. ]
[6.1 2.9 4.7 1.4]
[5.6 2.9 3.6 1.3]
[6.7 3.1 4.4 1.4]
[5.6 3. 4.5 1.5]
[5.8 2.7 4.1 1. ]
[6.2 2.2 4.5 1.5]
[5.6 2.5 3.9 1.1]
[5.9 3.2 4.8 1.8]
[6.1 2.8 4. 1.3]
[6.3 2.5 4.9 1.5]
[6.1 2.8 4.7 1.2]
[6.4 2.9 4.3 1.3]
[6.6 3. 4.4 1.4]
[6.8 2.8 4.8 1.4]
[6.7 3. 5. 1.7]
[6. 2.9 4.5 1.5]
[5.7 2.6 3.5 1. ]
[5.5 2.4 3.8 1.1]
[5.5 2.4 3.7 1. ]
[5.8 2.7 3.9 1.2]
[6. 2.7 5.1 1.6]
[5.4 3. 4.5 1.5]
[6. 3.4 4.5 1.6]
[6.7 3.1 4.7 1.5]
[6.3 2.3 4.4 1.3]
[5.6 3. 4.1 1.3]
[5.5 2.5 4. 1.3]
[5.5 2.6 4.4 1.2]
[6.1 3. 4.6 1.4]
[5.8 2.6 4. 1.2]
[5. 2.3 3.3 1. ]
[5.6 2.7 4.2 1.3]
[5.7 3. 4.2 1.2]
[5.7 2.9 4.2 1.3]
[6.2 2.9 4.3 1.3]
[5.1 2.5 3. 1.1]
[5.7 2.8 4.1 1.3]
[6.3 3.3 6. 2.5]
[5.8 2.7 5.1 1.9]
[7.1 3. 5.9 2.1]
[6.3 2.9 5.6 1.8]
[6.5 3. 5.8 2.2]
[7.6 3. 6.6 2.1]
[4.9 2.5 4.5 1.7]
[7.3 2.9 6.3 1.8]
[6.7 2.5 5.8 1.8]
[7.2 3.6 6.1 2.5]
[6.5 3.2 5.1 2. ]
[6.4 2.7 5.3 1.9]
[6.8 3. 5.5 2.1]
[5.7 2.5 5. 2. ]
[5.8 2.8 5.1 2.4]
[6.4 3.2 5.3 2.3]
[6.5 3. 5.5 1.8]
[7.7 3.8 6.7 2.2]
[7.7 2.6 6.9 2.3]
[6. 2.2 5. 1.5]
[6.9 3.2 5.7 2.3]
[5.6 2.8 4.9 2. ]
[7.7 2.8 6.7 2. ]
[6.3 2.7 4.9 1.8]
[6.7 3.3 5.7 2.1]
[7.2 3.2 6. 1.8]
[6.2 2.8 4.8 1.8]
[6.1 3. 4.9 1.8]
[6.4 2.8 5.6 2.1]
[7.2 3. 5.8 1.6]
[7.4 2.8 6.1 1.9]
[7.9 3.8 6.4 2. ]
[6.4 2.8 5.6 2.2]
[6.3 2.8 5.1 1.5]
[6.1 2.6 5.6 1.4]
[7.7 3. 6.1 2.3]
[6.3 3.4 5.6 2.4]
[6.4 3.1 5.5 1.8]
[6. 3. 4.8 1.8]
[6.9 3.1 5.4 2.1]
[6.7 3.1 5.6 2.4]
[6.9 3.1 5.1 2.3]
[5.8 2.7 5.1 1.9]
[6.8 3.2 5.9 2.3]
[6.7 3.3 5.7 2.5]
[6.7 3. 5.2 2.3]
[6.3 2.5 5. 1.9]
[6.5 3. 5.2 2. ]
[6.2 3.4 5.4 2.3]
[5.9 3. 5.1 1.8]]
y值如下,共有150行,其中0、1、2分别代表三类花:
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2]
上面的是 x 数据,下边的是 y 数据,我们可以看到此时的数据集是带有数据标签的,所以此时建立模型的目的就是首先用一部分的数据进行训练,然后用另一部分数据进行预测,并且与其已有的标签进行对比验证,判断其预测准确性。
2.数据集拆分
代码如下(示例):
from sklearn.model_selection import train_test_split
train_x,test_x,train_y,test_y = train_test_split(x,y,test_size=0.1,random_state=0)
数据集拆分是为了验证模型在训练集和测试集是否过拟合,使用train_test_split的目的是保证从数据集中均匀拆分出测试集。这里,简单把10%的数据集拿出来用作测试集。
test_size=0.1 是指拿出10%的数据用来做测试,test_size=0.2 就是拿出20%的数据集用来做测试。
3.模型建立

根据这个模板的话其实只要是机器学习中的算法都可以拿来套用这个模板,不同的就是算法的位置和模型的参数不同,不知道算法具体位置的话大家当然也可以用科技来AI一下了,比如我们要调用支持向量回归:
比如我们要调用AUC指标进行评价:

如果大家经常调用的话,每个包的存放位置都是有规律的,好多同类算法在一个集成包下。
#随机森林
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error, r2_score
model_rf = RandomForestRegressor(n_estimators=500, random_state=42)
model_rf.fit(X_train, y_train)
# 预测测试集
rf_pred = model_rf.predict(X_test)
# 计算MSE
rf_test_mse = mean_squared_error(y_test, rf_pred)
rf_test_rmse = np.sqrt(mean_squared_error(y_test, rf_pred))
# 计算R2分数
rf_test_r2 = r2_score(y_test, rf_pred)
from sklearn.svm import SVR
import numpy as np
# 拟合SVR模型
svr_rbf = SVR(kernel='rbf')
svr_rbf.fit(X_train, y_train)
from sklearn.metrics import mean_squared_error, r2_score
# 预测测试集
svr_rbf_pred = svr_rbf.predict(X_test)
# 计算MSE
svr_rbf_test_mse = mean_squared_error(y_test, svr_rbf_pred)
svr_rbf_test_rmse = np.sqrt(mean_squared_error(y_test, svr_rbf_pred))
# 计算R2分数
svr_rbf_test_r2 = r2_score(y_test, svr_rbf_pred)
4.模型改进方案2.0
在上一个版本当中,当你多次运行同一个程序就会发现:每次运行得到的精确度并不相同,而是在一定范围内浮动,这是因为数据输入模型之前会进行选择,每次训练时数据输入模型的顺序都不一样。所以即使是同一个程序,模型最后的表现也会有好有坏。
有些情况下,在训练集上,通过调整参数设置使模型的性能达到了最佳状态,但在测试集上却可能出现过拟合的情况。这个时候,我们在训练集上得到的评分不能有效反映出模型的泛化性能,这种情况下就是我们经常所说的过拟合问题,在训练数据集上通过调整模型参数等操作使得数据在训练集上的准确率达到了较高情况,但到了测试集上真正开始检验的时候准确率却没有那么高。
为了解决上述两个问题,还应该在训练集上划分出验证集(validation set)并结合交叉验证来解决。首先,在训练集中划分出不参与训练的验证集,只是在模型训练完成以后对模型进行评估,接着再在测试集上进行最后的评估。
但这样大大减少了可用于模型学习的样本数量,所以还需要采用交叉验证的方式多训练几次。比如说最常用的k-折交叉验证如下图所示,它主要是将训练集划分为 k 个较小的集合。然后将k-1份训练子集作为训练集训练模型,将剩余的 1 份训练集子集作为验证集用于模型验证。这样需要训练k次,最后在训练集上的评估得分取所有训练结果评估得分的平均值。
之所以说这样减少了可用于模型学习的样本数量是因为并不是所有的样本都用来训练,我们在进行模型训练的时候划分了一部分数据集用来与训练集的预测值进行比较,所以用来比较的这部分数据集是没有参与训练的,假如我们采用五折交叉验证的话进行过程如下图所示:
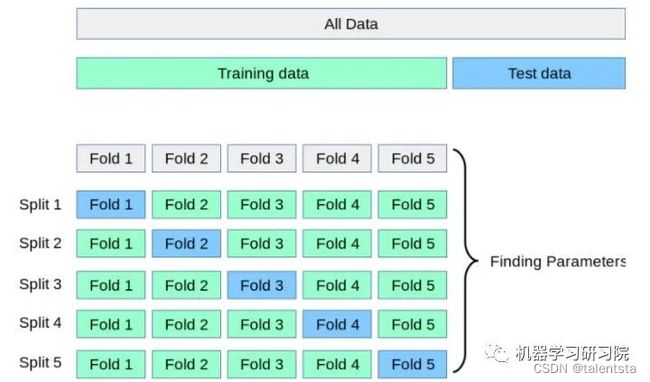
这时我们是将数据均匀的划分成五份,每次用四份来进行训练,一份来进行测试,执行五次,所以通过五折交叉验证我们相当于用五份数据都做了一次测试集,这样一方面可以让训练集的所有数据都参与训练,另一方面也通过多次计算得到了一个比较有代表性的得分。唯一的缺点就是计算代价很高,增加了k倍的计算量。
scikit-learn已经将优秀的数学家所想到的均匀拆分方法和程序员的智慧融合在了cross_val_score() 这个函数里了,只需要调用该函数即可,不需要自己想什么拆分算法,也不用写for循环进行循环训练。
在求精确度的时候,我们可以简单地输出平均精确度:
# 输出精确度的平均值
# print("训练集上的精确度: %0.2f " % scores1.mean())
但是既然我们进行了交叉验证,做了这么多计算量,单求一个平均值还是有点浪费了,可以利用下边代码捎带求出精确度的置信度:
# 输出精确度的平均值和置信度区间
print("训练集上的平均精确度: %0.2f (+/- %0.2f)" % (scores2.mean(), scores2.std() * 2))
以上说了那么多,下面让我们来看一下具体的应用案例:
### svm分类器
from sklearn.model_selection import cross_val_score
from sklearn.svm import SVC
svm_model = SVC()
svm_model.fit(train_x,train_y)
scores1 = cross_val_score(svm_model,train_x,train_y,cv=5, scoring='accuracy')
# 输出精确度的平均值和置信度区间
print("训练集上的精确度: %0.2f (+/- %0.2f)" % (scores1.mean(), scores1.std() * 2))
scores2 = cross_val_score(svm_model,test_x,test_y,cv=5, scoring='accuracy')
# 输出精确度的平均值和置信度区间
print("测试集上的平均精确度: %0.2f (+/- %0.2f)" % (scores2.mean(), scores2.std() * 2))
print(scores1)
print(scores2)
输出:
训练集上的精确度: 0.96 (+/- 0.09)
测试集上的平均精确度: 0.80 (+/- 0.13)
[0.95833333 0.95833333 1. 1. 0.875 ]
[0.66666667 0.83333333 0.83333333 0.83333333 0.83333333]
# LogisticRegression分类器
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
lr_model = LogisticRegression()
lr_model.fit(train_x,train_y)
scores1 = cross_val_score(lr_model,train_x,train_y,cv=5, scoring='accuracy')
# 输出精确度的平均值和置信度区间
print("训练集上的精确度: %0.2f (+/- %0.2f)" % (scores1.mean(), scores1.std() * 2))
scores2 = cross_val_score(lr_model,test_x,test_y,cv=5, scoring='accuracy')
# 输出精确度的平均值和置信度区间
print("测试集上的平均精确度: %0.2f (+/- %0.2f)" % (scores2.mean(), scores2.std() * 2))
print(scores1)
print(scores2)
输出:
训练集上的精确度: 0.95 (+/- 0.10)
测试集上的平均精确度: 0.93 (+/- 0.16)
[0.95833333 0.91666667 1. 1. 0.875 ]
[1. 1. 0.83333333 1. 0.83333333]
模型改进方案3.0
以上都是通过算法的默认参数来训练模型的,不同的数据集适用的参数难免会不一样,scikit-learn对于不同的算法也提供了不同的参数可以自己调节。本文目的是构建一个万能算法框架构建模板,所以,这里只介绍一下一个通用的自动化调参方法。
首先要明确的是,scikit-learn提供了算法().get_params()方法来查看每个算法可以调整的参数,比如说,我们想查看SVM分类器算法可以调整的参数,可以:
SVC().get_params()
{‘C’: 1.0, ‘break_ties’: False, ‘cache_size’: 200, ‘class_weight’: None, ‘coef0’: 0.0, ‘decision_function_shape’: ‘ovr’, ‘degree’: 3, ‘gamma’: ‘scale’, ‘kernel’: ‘rbf’, ‘max_iter’: -1, ‘probability’: False, ‘random_state’: None, ‘shrinking’: True, ‘tol’: 0.001, ‘verbose’: False}
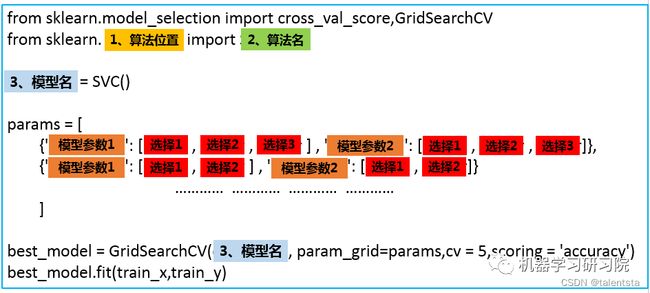
参数的形式如下:

程序就会按照顺序测试这几个参数的组合效果,根本不需要自己辛辛苦苦实现。假如我们要调节n个参数,每个参数有4个备选值。那么程序就会训练 4n 。当n为10的时候是 410 ,这是一个对于计算机来说庞大的计算量。而当我们将这10个参数拆分成5组,每次只调节两个参数,其他参数采用默认值,那么计算量就是5*4**2=80 ,计算量会大大减少。
列表的作用这是如此,保证了每次只调节列表中的一个字典中的参数。运行之后,best_model就是我们得到的最优模型,可以利用这个模型进行预测。
当然,best_model 还有好多好用的属性:
best_model.cv_results_:可以查看不同参数情况下的评价结果。
best_model.param_ :得到该模型的最优参数
best_model.best_score_: 得到该模型的最后评分结果
实现SVM分类器
###1、svm分类器
from sklearn.model_selection import cross_val_score,GridSearchCV
from sklearn.svm import SVC
svm_model = SVC()
params = [
{'kernel': ['linear'], 'C': [1, 10, 100, 100]},
{'kernel': ['poly'], 'C': [1], 'degree': [2, 3]},
{'kernel': ['rbf'], 'C': [1, 10, 100, 100], 'gamma':[1, 0.1, 0.01, 0.001]}
]
best_model = GridSearchCV(svm_model, param_grid=params,cv = 5,scoring = 'accuracy')
best_model.fit(train_x,train_y)
查看最优得分:
best_model.best_score_
0.9583333333333334
查看最优参数:
best_model.best_params_
{‘C’: 10, ‘kernel’: ‘linear’}
查看最优模型的所有参数:
best_model.best_estimator_
输出:
SVC(C=10, kernel=‘linear’)
这里对于线性核我们只设置了两个可以调节的参数,所以这里出现了两个参数。
这个函数会显示出没有调参的参数,便于整体查看模型的参数。
查看每个参数的交叉验证结果:
best_model.cv_results_
总结
这里简单介绍了数学建模经常会用到的一些操作以及基本流程步骤,基本的功能都可以实现了,当然还有很多其他部分还需要再细化,比如说数据处理部分,对于缺失值如何做到有效的填补以及如何由文字转为编码格式进行分析等,后续会进行更加详细的补充和分析。
