【C语言】浅_刷 —— 栈 - 队列 OJ题,看了就会~(详解版)
文章目录
- 前言
- 1. OJ练习
-
-
- 1.1 用队列实现栈
- 1.2 用栈实现队列
- 1.3 设计循环队列
-
- 总结
前言
上一篇简单的实现了一下队列,并介绍了队列的概念及结构。今天将带来三道OJ题练习,将继续对栈和队列的知识进行更深入的认识和巩固。
队列不清楚的小伙伴可以复习一下相关知识:
- 【数据结构】队列的基本操作(C语言版)
1. OJ练习
有了上面队列的结构,再加上之前实现的栈的结构,我们来做几道OJ练习来加强对知的理解。
1.1 用队列实现栈
OJ链接

本题并没有太大的逻辑结构,更多的反而是结构上的难度。
思路:
因为栈的结构规定了数据只能是后进先出,而本题却让我们用两个队列来实现。
基于队列存储数据的要求即先进先出的原则,就有了以下的思路:
- 将数据存储在非空的其中一个队列中(当两个队列都为空时,任意在存一个队列中),这样就实现了 “入栈” 。
- 删除数据(出栈)时,要满足后进的数据先出,所以要将非空的队列中的前n - 1个元素拷贝到空队列中,非空队列向空队列拷贝一个元素就要删除一个。最后还剩一个(即真正要删除的元素,也是题目中要求出栈的数据),这里还需要判断哪一个队列为空,具体过程看代码实现,再将剩的最后一个元素删除,就实现了 “出栈” 。
- 后续操作就是重复上述过程,直到数据删空为止。
- 实现了上述的过程,我们就实现了后存入的数据先出,先存入的数据后出,用两个 “队列” 实现了一个“栈” 。
- 最后释放空间时要注意:先将队列挨个释放再释放自己创造的栈,不然可能会造成**内存泄漏。
假设先插入1 , 2, 3 ,4 , 5这几个数。

下面是删除的过程:
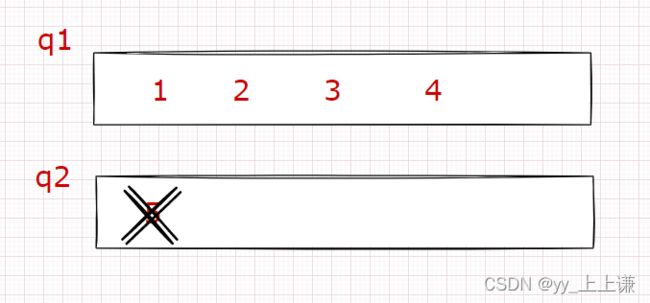

………………
直到将数据删空位止。
这里需要我们自己先实现一个队列来供我们调用。
参考代码如下:
typedef int QDataType;
typedef struct QueueNode
{
QDataType data;
struct QueueNode* next;
}QNode;
//记录头指针和尾指针
typedef struct Queue
{
QNode* head;
QNode* tail;
}Queue;
//队列的初始化
void QueueInit(Queue* pq);
//队列的销毁
void QueueDestroy(Queue* pq);
//入队
void QueuePush(Queue* pq, QDataType x);
//出队
void QueuePop(Queue* pq);
//判断队列是否为空
bool QueueEmpty(Queue* pq);
//队列中数据的个数
size_t QueueSize(Queue* pq);
//队头的数据
QDataType QueueFront(Queue* pq);
//队尾的数据
QDataType QueueBack(Queue* pq);
//队列的初始化
void QueueInit(Queue* pq)
{
assert(pq);
pq->head = pq->tail = NULL;
}
//队列的销毁
void QueueDestroy(Queue* pq)
{
QNode* cur = pq->head;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
}
//入队
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
exit(-1);
newnode->data = x;
newnode->next = NULL;
//尾插 - 用了尾指针就不用找尾了
if (pq->tail == NULL)
{
assert(pq->head == NULL);
pq->head = pq->tail = newnode;
}
else
{
pq->tail->next = newnode;
pq->tail = newnode;
}
}
//出队
void QueuePop(Queue* pq)
{
assert(pq);
assert(pq->head && pq->tail);
//头删 - 只有一种个结点的情况时tail会成野指针
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else
{
QNode* next = pq->head->next;
free(pq->head);
pq->head = next;
}
}
//判断队列是否为空
bool QueueEmpty(Queue* pq)
{
assert(pq);
return pq->head == NULL && pq->tail == NULL;
}
//队列中数据的个数
size_t QueueSize(Queue* pq)
{
assert(pq);
QNode* cur = pq->head;
size_t size = 0;
while (cur)
{
size++;
cur = cur->next;
}
return size;
}
//队头的数据
QDataType QueueFront(Queue* pq)
{
assert(pq);
assert(pq->head);
return pq->head->data;
}
//队尾的数据
QDataType QueueBack(Queue* pq)
{
assert(pq);
assert(pq->tail);
return pq->tail->data;
}
typedef struct
{
Queue q1;
Queue q2;
} MyStack;
MyStack* myStackCreate()
{
MyStack* pst = (MyStack*)malloc(sizeof(MyStack));
if(pst == NULL)
exit(-1);
QueueInit(&pst->q1);
QueueInit(&pst->q2);
return pst;
}
void myStackPush(MyStack* obj, int x)
{
assert(obj);
if(!QueueEmpty(&obj->q1))
{
QueuePush(&obj->q1, x);
}
else
{
QueuePush(&obj->q2, x);
}
}
int myStackPop(MyStack* obj)
{
assert(obj);
Queue* empty = &obj->q1;
Queue* nonEmpty = &obj->q2;
if(!QueueEmpty(empty))
{
empty = &obj->q2;
nonEmpty = &obj->q1;
}
while(QueueSize(nonEmpty) > 1)
{
QueuePush(empty,QueueFront(nonEmpty));
QueuePop(nonEmpty);
}
int top = QueueBack(nonEmpty);
QueuePop(nonEmpty);
return top;
}
int myStackTop(MyStack* obj)
{
assert(obj);
if(!QueueEmpty(&obj->q1))
{
return QueueBack(&obj->q1);
}
else
{
return QueueBack(&obj->q2);
}
}
bool myStackEmpty(MyStack* obj)
{
assert(obj);
return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}
void myStackFree(MyStack* obj)
{
assert(obj);
QueueDestroy(&obj->q1);
QueueDestroy(&obj->q2);
free(obj);
}
/**
* Your MyStack struct will be instantiated and called as such:
* MyStack* obj = myStackCreate();
* myStackPush(obj, x);
* int param_2 = myStackPop(obj);
* int param_3 = myStackTop(obj);
* bool param_4 = myStackEmpty(obj);
* myStackFree(obj);
*/
1.2 用栈实现队列
OJ链接

思路:
因为队列的结构规定了数据只能是先进先出,而本题却让我们用两个栈来实现。
基于队列存储数据的要求即先进先出的原则,就有了以下的思路:
- 定义两个栈,一个用来存放数据(pushST),一个用来专门删除数据(popST)。
- 只要是插入数据就将数据放在(pushST)这个栈中,只要是删除数据就从(popST)这个栈中删除数据。如果(popST)为空,就将(pushST)这个栈的数据导入到(popST)这个栈中。
- 将(pushST)这个栈的数据导入到(popST)这个栈中,这个过程因为栈是 “后进先出” 的,所以“导入” 的这一个过程中是从(pushST)这个栈的 “栈顶依次 拿出数据放到(popST)这个栈中,所以(popST)这个栈中的数据存放的顺序是和原本(pushST) 栈中数据存放的顺序是 “相反的” 。 这时候从(popST)这个栈出栈就是相当于将原本(pushST)这个栈中的数据的前面的数据删除。
- 实现了上述的过程,我们就实现了先存入的顺序先出,后存入的数据后出,用两个栈实现了一个队列。
- 最后释放空间时要注意:先将队列挨个释放再释放自己创造的栈,不然可能会造成**内存泄漏。
假设先插入1 , 2, 3 ,4 , 5这几个数。
插入和删除过程如下图:


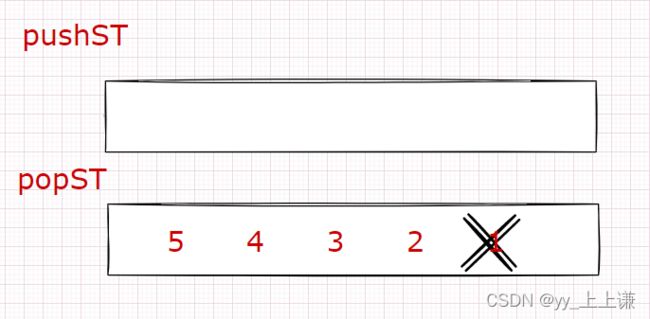

此时再出入两个数据

下面继续删除 ………………
假设(popST)这个栈的数据都已经删完了。
那么就将(pushST)这个栈中的数据导入到(popST)这个栈中。
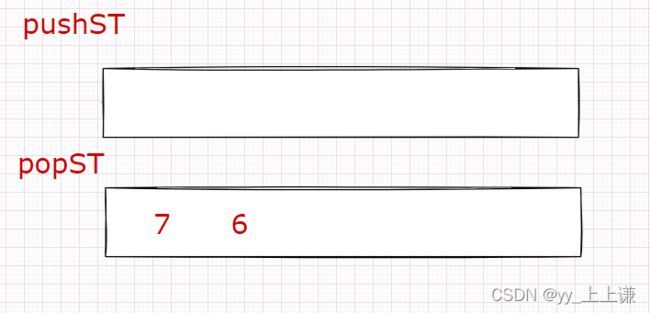
下面继续进行上述删除过程。
这里需要我们自己先实现一个栈来供我们调用。
参考代码如下:
typedef int STDataType;
typedef struct Stack
{
int* a;
int top; //栈顶的位置
int capacity; //容量
}ST;
//初始化
void StackInit(ST* ps);
//销毁
void StackDestroy(ST* ps);
//进栈
void StackPush(ST* ps, STDataType x);
//出栈
void StackPop(ST* ps);
//判断栈是否为空
bool StackEmpty(ST* ps);
//栈顶的数据
STDataType StackTop(ST* ps);
//栈的数据个数
int StackSize(ST* ps);
//初始化
void StackInit(ST* ps)
{
assert(ps);
ps->a = NULL;
ps->top = 0;
ps->capacity = 0;
}
//销毁
void StackDestroy(ST* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->capacity = ps->top = 0;
}
//进栈
void StackPush(ST* ps, STDataType x)
{
assert(ps);
//满了扩容
if (ps->top == ps->capacity)
{
int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
int* tmp = (int*)realloc(ps->a, newCapacity * sizeof(STDataType));
if (tmp == NULL)
exit(-1);
ps->a = tmp;
ps->capacity = newCapacity;
}
ps->a[ps->top] = x;
ps->top++;
}
//出栈
void StackPop(ST* ps)
{
assert(ps);
assert(ps->top > 0);
ps->top--;
}
//判断栈是否为空
bool StackEmpty(ST* ps)
{
assert(ps);
/*if (ps->top > 0)
{
return false;
}
else
{
return true;
}*/
return ps->top == 0;
}
//栈顶的数据
STDataType StackTop(ST* ps)
{
assert(ps);
assert(ps->top > 0);
return ps->a[ps->top - 1];
}
//栈的数据个数
int StackSize(ST* ps)
{
assert(ps);
return ps->top;
}
typedef struct
{
ST pushST;
ST popST;
} MyQueue;
MyQueue* myQueueCreate()
{
MyQueue* pst = (MyQueue*)malloc(sizeof(MyQueue));
if(pst == NULL)
exit(-1);
StackInit(&pst->pushST);
StackInit(&pst->popST);
return pst;
}
void myQueuePush(MyQueue* obj, int x)
{
assert(obj);
StackPush(&obj->pushST, x);
}
int myQueuePop(MyQueue* obj)
{
assert(obj);
int front = 0;
if(StackEmpty(&obj->popST))
{
while(StackSize(&obj->pushST) > 0)
{
StackPush(&obj->popST, StackTop(&obj->pushST));
StackPop(&obj->pushST);
}
front = StackTop(&obj->popST);
StackPop(&obj->popST);
}
else
{
front = StackTop(&obj->popST);
StackPop(&obj->popST);
}
return front;
}
int myQueuePeek(MyQueue* obj)
{
assert(obj);
if(StackEmpty(&obj->popST))
{
while(StackSize(&obj->pushST) > 0)
{
StackPush(&obj->popST,StackTop(&obj->pushST));
StackPop(&obj->pushST);
}
}
return StackTop(&obj->popST);
}
bool myQueueEmpty(MyQueue* obj)
{
assert(obj);
return StackEmpty(&obj->popST) && StackEmpty(&obj->pushST);
}
void myQueueFree(MyQueue* obj)
{
assert(obj);
free((&obj->popST)->a);
free((&obj->pushST)->a);
free(obj);
}
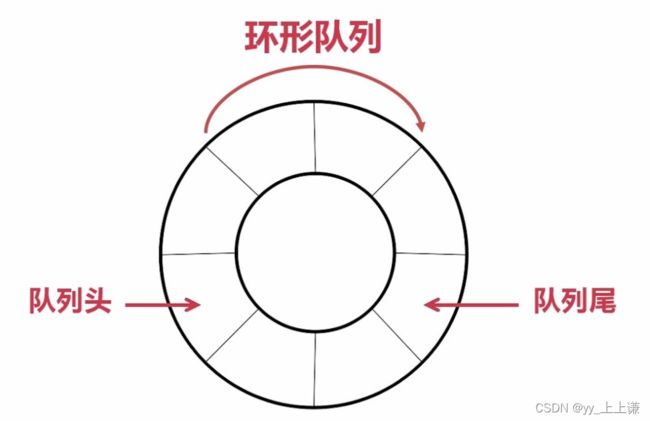
1.3 设计循环队列
- 数组式环形队列
- 链表式环形队列
这里我们选用数组实现环形队列,因为是环形结构且又是队列,那么删除数据肯定满足先进先出,如果用链式结构的话,那就要设计环形链表,当删除数据时环形链表的头在更新,插入数据时需要找尾的前一个结点,对于单链表来说找前驱是很麻烦的过程。
综上所述:我们选用数组式环形队列。

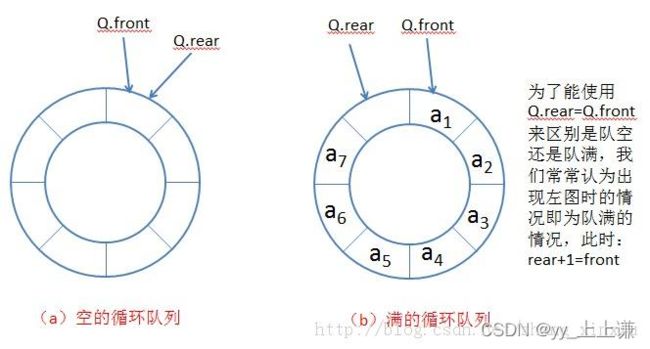
当front == tail时为空,假设环形队列的大小为k
具体思路:
- 插入一个数据那么tail就向后挪动一个单位,当tail == k - 1时,下一步就将k赋值成0,那么tail又指向了下标为0的位置,这样就形成了循环的结构。
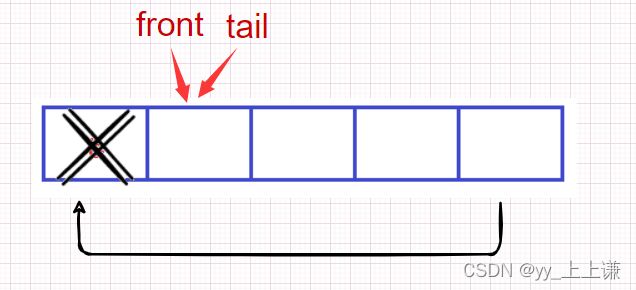
但是这种结构会出现问题:先插入,再删除,再插入的时候会出现如图所示的情况:
先插入1 ,2,3, 4,再删除一个(将1删除),再插入一个5(即在循环队列的头插入一个5)

因为tail永远指向循环队列最后一个元素的后一个位置,所以就会出现这种队列实则满却被条件(tail == front)判为空的情况。
解决方案:
我们在对数开辟空间的时候多开一个空间,这样就能很好的错开,避免了上面的情况。
存入的有效数据为k个,但是我们开辟数组的时候开辟(k + 1)个空间,有一个空间始终是不存放数据的。
- 当(front == tail)的时候,循环队列为空。
- 当(fornt == tail + 1)的时候队列为满。
下面举两个满了的栗子:
满了的情况1:
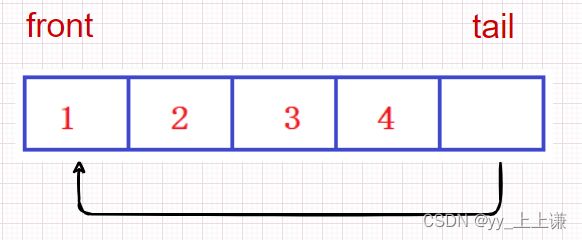
满了的情况2:

以上情况均符合(tail)的下一个位置为(front)的条件。
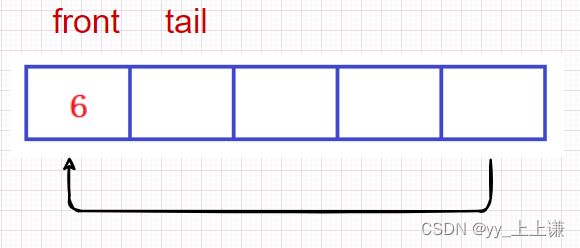
假设只存储了一个数据:
typedef struct
{
int front;
int tail;
int k;
int* a;
} MyCircularQueue;
bool myCircularQueueIsEmpty(MyCircularQueue* obj);
bool myCircularQueueIsFull(MyCircularQueue* obj);
MyCircularQueue* myCircularQueueCreate(int k)
{
MyCircularQueue* pst = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
if(pst == NULL)
exit(-1);
pst->a = (int*)malloc(sizeof(int) * (k + 1));
if(pst->a == NULL)
exit(-1);
pst->front = pst->tail = 0;
pst->k = k;
return pst;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value)
{
assert(obj);
if(myCircularQueueIsFull(obj))
return false;
if(obj->tail == obj->k)
{
obj->a[obj->tail] = value;
obj->tail = 0;
}
else
{
obj->a[obj->tail++] = value;
}
return true;
}
bool myCircularQueueDeQueue(MyCircularQueue* obj)
{
assert(obj);
if(myCircularQueueIsEmpty(obj))
return false;
if(obj->front == obj->k)
{
obj->front = 0;
}
else
{
obj->front++;
}
return true;
}
int myCircularQueueFront(MyCircularQueue* obj)
{
assert(obj);
if(myCircularQueueIsEmpty(obj))
return -1;
return obj->a[obj->front];
}
int myCircularQueueRear(MyCircularQueue* obj)
{
assert(obj);
if(myCircularQueueIsEmpty(obj))
return -1;
if(obj->tail == 0)
{
return obj->a[obj->k];
}
else
{
return obj->a[obj->tail - 1];
}
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj)
{
assert(obj);
return obj->front == obj->tail;
}
bool myCircularQueueIsFull(MyCircularQueue* obj)
{
assert(obj);
if(obj->front == 0 && obj->tail == obj->k)
{
return true;
}
else
{
return obj->tail + 1 == obj->front;
}
}
void myCircularQueueFree(MyCircularQueue* obj)
{
assert(obj);
free(obj->a);
free(obj);
}
总结
多画图有利于解题,弄清细节很重要!