树、森林与二叉树的转换
文章目录
-
- 一.转换
-
- 1.树 ⟷ \longleftrightarrow ⟷二叉树
- 2.森林 ⟷ \longleftrightarrow ⟷二叉树
- 题——空指针计算:
- 二.遍历
-
- 1.树:
- 2.森林:
- 三.树练习
-
- 1.求树叶子结点个数
- 2.求树高
树——逻辑结构,其存储结构有顺序、链式存储。
树的三种表示法:
1.双亲表示法——顺序存储,每个结点包括:结点值
data、双亲的下标 parent。一般用数组实现。
2.孩子表示法——链式存储,将每个结点的孩子用单链表连接起来。
3. 孩子兄弟表示法——链式存储(二叉树表示法),每个结点包括:结点值
data、指向第一个孩子的指针 firstchild,指向结点下一个兄弟的指针 nextsibling。
一.转换
- 树、森林、二叉树 之间的转化是 唯一的
1.树 ⟷ \longleftrightarrow ⟷二叉树
(1)树 → \rightarrow →二叉树
- 将所有兄弟相连
- 保留指向第一个孩子的指针,抹去其他
- 以根为轴心顺时针转45°(即将所有兄弟变成右子)
实际上是一个,从上到下,从左到右的右兄变右子的过程。
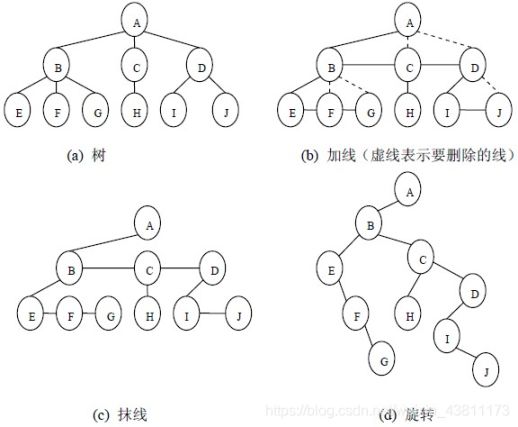
树的先跟、二叉树的先序均为:ABEFGCHDIJ
树的后跟、二叉树的中序均为:EFGBHCIJDA
(2)二叉树 → \rightarrow →树
从上到下,依次将所有结点的右子变成其的右兄弟即可。
2.森林 ⟷ \longleftrightarrow ⟷二叉树
森林即一些树的集合。
(1)森林 → \rightarrow →二叉树
- 将每棵树转化成二叉树
- 将每棵树的根视为兄弟结点,依次连接
- 以第一颗树的根为轴心旋转45°(即将右兄(根)变右子)
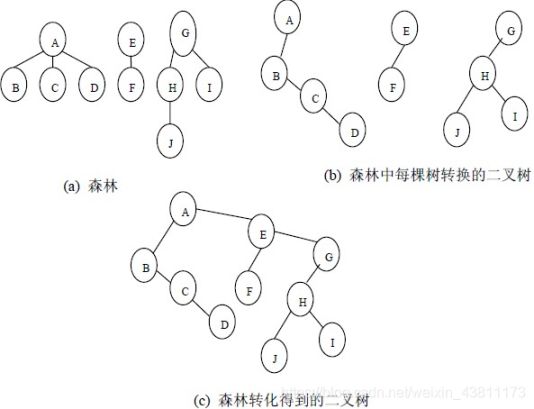
森林、二叉树的先序均为:ABCDEFGHJI
森林、二叉树的中序均为:BCDAFEJHIG
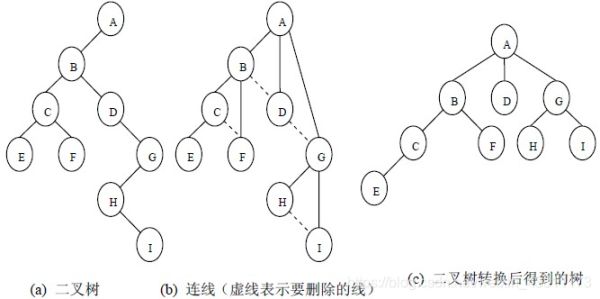
(2)二叉树 → \rightarrow →森林
1.从上到下,每次将根的右链断开,得到一些二叉树
2.将所有二叉树转化成树,得到森林
题——空指针计算:
树/森林 的叶结点数: n 1 n_1 n1,非终端结点数: n 2 n_2 n2,则转换成二叉树后
左子为空结点数: n 1 n_1 n1,右子为空结点数: n 2 + 1 n_2+1 n2+1
左子为空 = 叶结点数
树/森林:只有叶结点没有孩子,转化成二叉树后,左子为空,所以是 n 1 n_1 n1
右子为空 = 非叶结点数 + 1(根)
树/森林:每个非叶结点都有孩子,其最右边的孩子必然无右兄,即转换成二叉树后必然右子为空, n 2 n_2 n2个右子为空
树:树的根无右兄,故 n 2 + 1 n_2+1 n2+1
森林:森林的根视为兄弟相连,其最右边的根无右兄,故也是 n 2 + 1 n_2+1 n2+1
2011统考真题:2011个结点的树,叶结点数为116,其对应的二叉树中无右孩子节点的个数是:2011-116+1 = 1896
2014统考真题:森林F转换成二叉树T后,F中叶结点个数等于:T中左孩子指针为空的结点个数
树的 结点数=边数+1(结点数=总度数+1)
所以 森林中的 总结点数-总边数=森林中树的个数
2016统考真题:若森林F有15条边,25个结点,则F包含树的个数:25-15=10
二.遍历
1.树:
先根遍历:先访问根,再访问子树。对树的每一棵子树递归进行。
后跟遍历:先访问子树,后访问根。递归进行。
2.森林:
先序遍历:先访问第一棵树的根节点,先序遍历第一棵树根节点的子树森林,先序遍历第一棵树外其他树组成的森林。
中序遍历:中序遍历第一棵树的根节点的子树森林,访问第一棵树的根节点,中序遍历第一棵树外其他树组成的森林。
先根:根子
后根:子根
先序遍历森林:对每棵树依次进行先跟遍历
中序遍历森林:对每棵树依次进行后根遍历
| 树 | 森林 | 二叉树 |
|---|---|---|
| 先跟 | 先序 | 先序 |
| 后跟 | 中序 | 中序 |
等价关系:
树先根 = 森林先序 = 二叉树先序
树后根 = 森林中序 = 二叉树中序
2019统考真题 将树T转换成二叉树BT,则与T的后跟遍历相同的是:BT的中序遍历
三.树练习
1.求树叶子结点个数
孩子兄弟链表为存储结构。
int Q5(Tree T) {
if (T == NULL)
return 0;
if(T->child==NULL) //没有孩子的时候,说明是叶结点
return Q5(T->sibling) + 1;
else
return Q5(T->sibling) + Q5(T->child);
}
2.求树高
孩子兄弟链表为存储结构。
int Q6(Tree T) {
if (T == NULL)
return 0;
else
return Q6(T->child) + 1 > Q6(T->sibling) ? Q6(T->child) + 1 : Q6(T->sibling);
}
一般二叉树的递归求高为
return Q(T->lchild) > Q(T->rchild) ? Q(T->lchild) + 1 : Q(T->rchild) + 1;