sea_bi

算法和数据结构

程序 = 算法 + 数据结构

在刷题的时候遇到数据结构知识不够，特来补充学习。

前言

开始学习数据结构。

不要轻视基础算法和数据结构，而只关注“有意思”的题目
各种排序算法：
基础数据结构和算法的实现：如堆、二叉树、图等
基础数据结构的使用：如链表、栈、队列、哈希表、图、Trie、并查集等
基础算法：深度优先、广度优先、递归、二分查找等
基本算法思想：递归、分治、动态规划、贪心、回溯搜索等

1 字符串

1.1 剑指offer例题

字符串常考的题目。

1.1.1 【剑指Offer】2、替换空格

题目描述：
请实现一个函数，将一个字符串中的每个空格替换成“%20”。例如，当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
思路：第一个想到的就是用python中的replace方法：
str.replace(old, new[, max]) ，把字符串中的 old（旧字符串）替换成 new(新字符串)，如果指定第三个参数max，则替换不超过 max 次。

采用调包。

class Soultion:
    def replace(self,s):
        s=s.replace(" ","%20")
        return s


if __name__ == "__main__":
    s = Soultion()
    res = s.replace("We Are Happy")
    print(res)

输出：
We%20Are%20Happy

1.1.2 验证回文串

回文串（palindromic string）是指这个字符串无论从左读还是从右读，所读的顺序是一样的；简而言之，回文串是左右对称的。所谓最长回文子串问题，是指对于一个给定的母串。

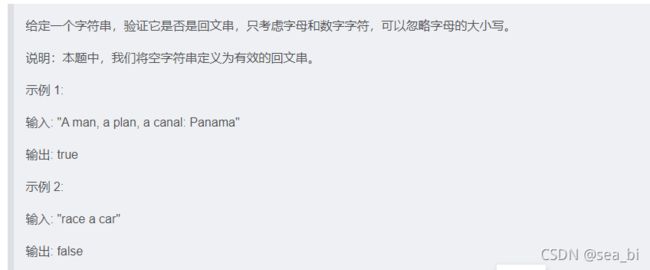
def isPalindrome(str):
    if not str:
        return True
    beg = 0
    end = len(str)-1
    while beg < end:
        if not str[beg].isalnum():
            beg += 1
            continue
        if not str[end].isalnum():
            end -= 1
            continue
        if str[beg].lower() == str[end].lower():
            beg += 1
            end -= 1
        else:
            return False
    return True


if __name__ == '__main__':
    tempt = "A man, a plan, a canal: Panama"
    print(isPalindrome(tempt))

输出是：True

1.1.3

2 数组和列表

2.1 数组 array

推荐你用 numpy.array

2.2 列表 list

1、列表操作平均时间复杂度
list[index] O(1)
list.append O(1)
list.insert O(n)
list.pop(index), default last element O(1)
list.remove O(n)

2.3 剑指offer例题

2.3.1【剑指Offer】1、二维数组中的查找

例如：
找数字7的过程：
[[1,2,3,4,5],
↓
[3,4,5,6,7],
[8,9,10,11,12]]

代码实现：

class Soultion:
    def find(self, target, arr):
        len_row = len(arr) - 1 # 行的长度范围
        len_col = len(arr[0]) - 1 # 列的长度范围

        i = 0 # 从右上角开始，二维数组索引为array[0][len_col]
        j = len_col # 用i，j来查找数组中的元素，i对应行，j对应列
        while i <= len_row and j >= 0:
            if arr[i][j] == target:
                return True
            # 如果没找到且当前array[i][j]数值比target小,继续向下查找
            elif arr[i][j] < target:
                i += 1
            # 如果没找到且当前array[i][j]数值比target大,向 查找
            else:
                j -= 1
        # 搜索到数组边界也没找到target，说明没有，返回false
        return False


if __name__ == "__main__":
    s = Soultion()
    arr = [[1, 2, 3, 4, 5],
           [3, 4, 5, 6, 7],
           [8, 9, 10, 11, 12]]
    res = s.find(7, arr)
    print(res)

输出：True

2.3.2 【剑指Offer】6、旋转数组的最小数字

题目描述：
把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个非减排序的数组的一个旋转，输出旋转数组的最小元素。例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。 NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

解题思路：
本题的直观解法很简单，直接对数组进行一次遍历就可以找到最小值，复杂度为O(n)，但是显然这不是本题的意图所在，因为没有利用到任何旋转数组的特性。
进一步分析，如果整个数组是有序的，那我们一定会想到用折半查找来实现（二分查找法）。对于旋转数组，我们发现，它实际上可以划分为两个排序的子数组，而且前面数组的元素都不小于后面数组的元素，并且最小值正好就是这两个数组的分界线，由此，我们可以得出以下解决方法。
首先用两个指针low和high分别指向数组的第一个元素和最后一个元素，然后可以找到中间元素mid。对于这个中间元素，有以下两种情况：（1）该元素大于等于low指向的元素，此时最小的元素说明在mid的后面，可以把low=mid；（2）中间元素小于等于high指向的元素，那么最小元素在mid之前，可以high=mid。特别注意：这里不要+1或者-1，因为只有这样才能保证low始终在第一个数组，high始终在第二个数组。依次循环，当最后low和high相差1时，low指向第一个数组的最后一个，high指向第二个数组的第一个（即为我们要找的最小值）。很明显，以上查找的时间复杂度为O(logN)。

这一题隐藏信息是有序，对于有序数列通常使用二分查找法比较有效。

用low代表数组低起点位置，high代表数组高起点位置，mid = (low + high) / 2是数组中间位置。
这时候有几种情况：
1、当中间元素比最右侧元素大的时候，说明最小元素一定在右侧，令low = mid + 1 （因为这个时候最小值一定不是mid了所以low可以等于mid+1)：

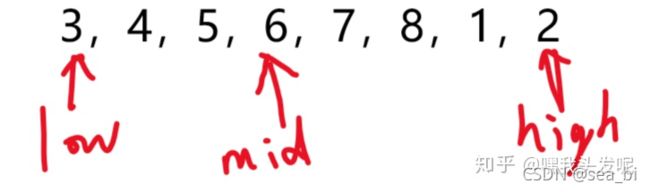
2、当中间元素比最右侧元素小的时候，说明最小元素要么是mid要么是在左边，因为右侧呈一个递增序列，所以这个时候让high=mid：

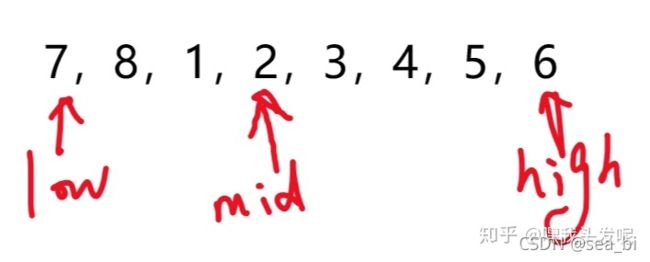
3、当中间元素等于最右侧元素时，说明出现了数值相等的情况，这个时候无法判断最小元素出现在左侧或者右侧，一个办法是，既然这两个元素相等，那就说明都不是最小的元素，所以让high的位置左移，继续查找，一种可能的情况如下：

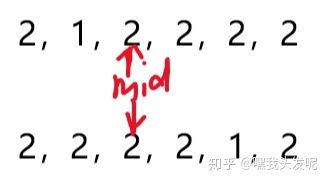
二分查找算法实现：题目说的是有序

class Solution:
    def minNumberInRotateArray(self, r):
        if len(r)==0:
            return 0
        if len(r)==1:
            return r[0]
        low=0
        high=len(r)-1
        while low<=high:
            mid=(low+high)//2
            if r[mid]>r[high]:
                low+=1
            elif r[mid] < r[high]:
                high=mid #为了不遗漏最小值，版呢个使用mid-1代替
            else:
                high-=1
        return r[mid]

if __name__ == "__main__":
    s=Solution()
    #插入数据
    mid=s.minNumberInRotateArray([3,4,5,1,2])
    print(mid)

输出：
1

2.3.3【剑指Offer】13、调整数组顺序使奇数位于偶数前面

题目描述：
输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分，并保证奇数和奇数，偶数和偶数之间的相对位置不变。
思路：
[1,2,3,4,5,6] # before
[1,3,5,2,4,6] # after
这个可以考虑用空间换时间，开辟两个数组，一个存放奇数一个存放偶数，到结果返回的时候合并起来。比较投机~

class Solution:
    def reOrderArray(self, array):
        even, odd = [], []
        for i in range(len(array)):
            if array[i] % 2 != 0:
                odd.append(array[i])
            else:
                even.append(array[i])
        return odd+even

解法2：
首先，如果不考虑奇数和奇数，偶数和偶数的相对位置，那么我们有一种双指针解法来求解，类似于快排，维护两个指针，第一个指针指向数组的第一个数字，第二个指针指向数组的最后一个数字。第一个指针向后移，第二个指针向前移，如果第一个指针指向偶数，第二个指针指向的是奇数，则交换着两个数字，接着继续移动直到两指针相遇。
上面的方法看似不错，但是对本题不适用，因为本题有相对位置不变的要求，直接交换会导致相对位置改变。因此，我们采用下面的思路来解决本题。
本题解法：对数组进行遍历，设置两个指针even和odd，even指向当前第一个偶数，odd从这个偶数之后开始查找，找到第一个奇数，此时为了相对位置不变，不能直接交换even和odd，而是将从even到odd-1的元素都依次向后移一个位置，将odd指向的那个奇数放到even的位置。然后再找下一个偶数，重复这一过程，最终就可以将奇数都放到偶数的前面，并且保证了相对位置的不变。

 public void reOrderArray(int [] array) {
        int len=array.length;
        int even=0,odd=0; //当前序列的第一个奇数和第一个偶数
        while(odd<len && even<len){
            while(even<len && array[even]%2!=0) //找到第一个偶数even
                even++;
            odd=even+1;
            //找偶数之后的第一个奇数
            while(odd<len && array[odd]%2==0)
                odd++;
            if(odd>=len)  //注意判断，防止溢出
                break;
            //把奇数取出来，从even到odd-1的元素都向后移
            int temp=array[odd];
            for(int i=odd;i>even;i--)
                array[i]=array[i-1];
            array[even]=temp; //奇数放在原来even的位置
            even++;
        }
    }

解法3：
考虑插入排序，如果是奇数就插入到第一个遇到的偶数前面

  private static int[] reOrderArray(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            // 遇到奇数就放到最前面
            if (Math.abs(arr[i]) % 2 == 1) {
                int temp = arr[i];
                // 先把 i 前面的都向后移动一个位置
                for (int j = i; j > 0; j--) {
                    arr[j] = arr[j - 1];
                }
                arr[0] = temp;
            }
        }
        return arr;
    }

2.3.4 【剑指Offer】19、顺时针打印矩阵

题目描述：
输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字，例如，如果输入如下4 X 4矩阵： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.

解题思路：
由于是按照从外到内的顺序依次打印，所以可以把矩阵想象成若干个圈，用一个循环来打印矩阵，每次打印矩阵中的一圈。假设矩阵的行数是row，列数是col，则每次都是从左上角开始遍历，而我们注意到左上角行标和列标总是相同的，假设是start，那么循环继续的条件就是row>start * 2 && col > start * 2。
而对于每一圈的打印，很自然便可以想到遵循从左到右，从上到下，从右到左，从下到上的顺序。但是这里需要注意的是最后一圈的打印，由于矩阵并不一定是方阵，最后一圈有可能退化为只有一行，只有一列，甚至只有一个数，因此要注意进行判断，避免重复打印。

这种解法好像还是不是太清晰。在其他地方还找到一个快捷的方法，首先定义矩阵的逆时针90°旋转，transpose方法先存储每一列数据，再倒序输出：
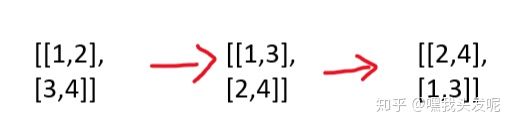然后当矩阵不为空的时候，每次把第一行结果存储到res当中，然后pop第一行，再transposr矩阵！
这里注意，如果matrix在最后一个元素执行的时候，pop完了就时空的，但是matrix还是会尝试执行transpose就会报错。需要在transpose前面用if判断一下跳出while循环~

class Solution:
    # matrix类型为二维列表，需要返回列表
    def transpose(self, matrix):
            new_matrix = []
            for i in range(len(matrix[0])): # 列
                matrix1 = []
                for j in range(len(matrix)): #行
                    matrix1.append(matrix[j][i])
                new_matrix.append(matrix1)
            return new_matrix[::-1]
    def printMatrix(self, matrix):
        res = []
        while matrix:
            res += matrix[0]
            matrix.pop(0)
            if not matrix:
                break
            matrix = self.transpose(matrix)
        return res

if __name__ == "__main__":
    s=Solution()
    t=s.printMatrix([[1,2,3],[4,5,6],[7,8,9]])
    print(t)

输出：
[1, 2, 3, 6, 9, 8, 7, 4, 5]

3 线性查找

3.1 实现线性表顺序存储的插入操作

def insertlist(L, i, item):
    n = len(L)
    if i < 0 or i > n:
        return False
    else:
        tempt_list = list(range(i - 1, n))
        # 采用从最后一位进行平移
        for j in tempt_list[::-1]:
            L[j + 1:j + 2] = [L[j]]
            # print(L)
        L[i - 1] = item
    return L


# 方法2：
def insert_list(L, i, item):
    n = len(L)
    if i < 0 or i > n:
        return False
    else:
        L.insert(i, item)
        return L


if __name__ == '__main__':
    L = [2, 6, 7, 8, 0]
    i = 2
    item = 99
    res = insertlist(L, i, item)
    print(res)

Python中list赋值时， L1=L 与 L1=L[:] 有什么区别？
严格的说，python没有赋值，只有名字到对象的绑定。所以L1=L是把L所指的对象绑定到名字L1上，而L2=L[:]则是把L通过切片运算取得的新列表对象绑定到L2上。前者两个名字指向同一个对象，后者两个名字指向不同对象。换句话说，L1和L是指的同一个东西，那么修改L1也就修改了L；L2则是不同的东西，修改L2不会改变L。注意这个引用的概念对于所有的东西都成立，例如容器内部存储的都是引用……

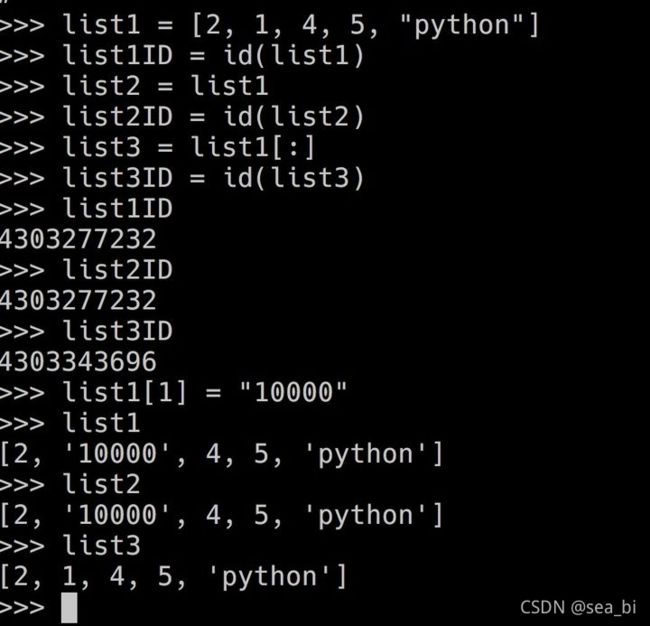
很容易理解了吧,

L1=L 意思是将L1也指向L的内存地址,

L1=L[:] 意思是, 复制L的内容并指向新的内存地址.

3.2 实现线性表顺序存储的删除操作

def delete_list(L, i):
    n = len(L)
    if i < 0 or i > n:
        return False
    else:
        # del L[i]
        for k in range(i-1, n - 1)[::1]:
            L[k] = L[k + 1]
            # print(L)
        L.pop()
    return L


if __name__ == '__main__':
    L = [2, 6, 7, 8, 1]
    i = 1
    res = delete_list(L, i)
    print(res)

4 排序基础

4.1 冒泡排序

冒泡排序（Bubble Sort）也是一种简单直观的排序算法。
它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。

运行流程：
1、比较相邻的元素。如果第一个比第二个大（升序），就交换他们两个。
2、对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
3、针对所有的元素重复以上的步骤，除了最后一个。
4、持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

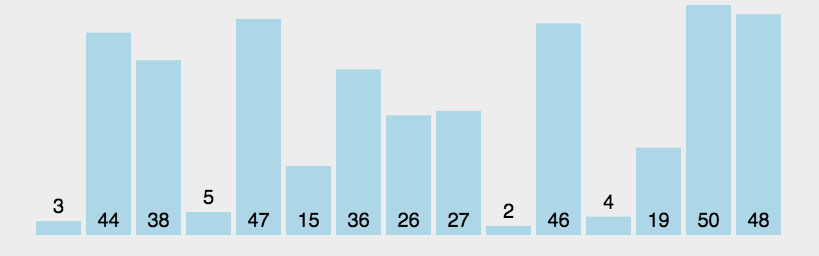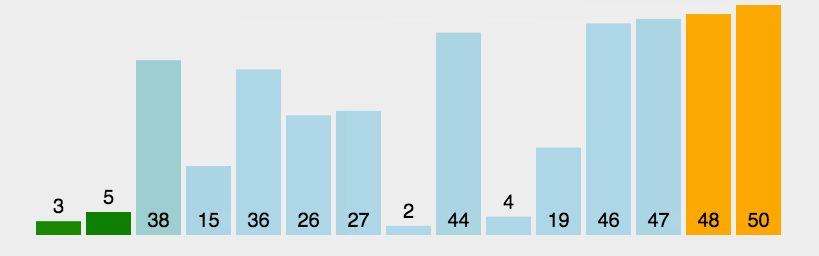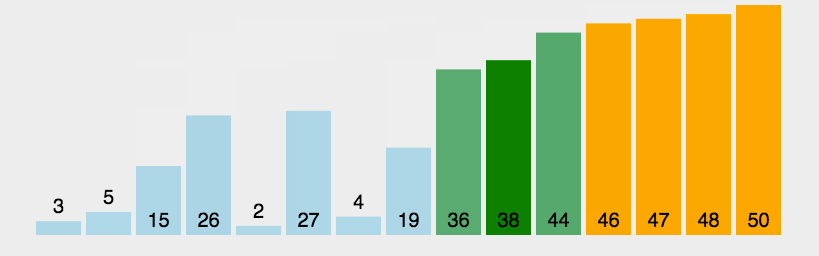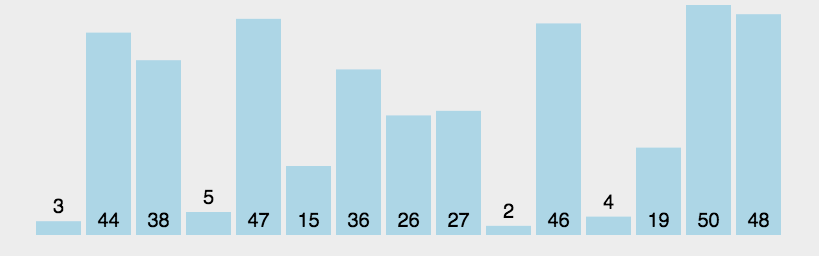
冒泡排序就是把小的元素往前调或者把大的元素往后调，比较是相邻的两个元素比较，交换也发生在这两个元素之间。（类似于气泡上浮过程）

# -*- coding:utf-8 -*-
"""
冒泡算法：多次遍历列表，将不合顺序的进行交换，一轮遍历将最大值放在列表最后面，

"""
def sortBubble(alist):
    al=len(alist)-1
    while al>0:
        for i in range(al):
            if alist[i]>alist[i+1]:
                alist[i],alist[i+1]= alist[i+1],alist[i]
        al-=1
    return alist

if __name__ == "__main__":
    res= sortBubble([2,5,3,8,2,6,4])
    print(res)

时间复杂度
最优时间复杂度：O(n) （表示遍历一次发现没有任何可以交换的元素，排序结束。）
最坏时间复杂度：O(n^2)
稳定性：稳定
排序分析：待排数组中一共有6个数，第一轮排序时进行了5次比较，第二轮排序时进行了4比较，依次类推，最后一轮进行了1次比较。

数组元素总数为N时，则一共需要的比较次数为：(N-1)+ (N-2)+ (N-3)+ …1=N*(N-1)/2
算法约做了N^{2/2次比较。因为只有在前面的元素比后面的元素大时才交换数据，所以交换的次数少于比较的次数。如果数据是随机的，大概有一半数据需要交换，则交换的次数为N}2/4（不过在最坏情况下，即初始数据逆序时，每次比较都需要交换）。
交换和比较的操作次数都与 N^2 成正比，由于在大O表示法中，常数忽略不计，冒泡排序的时间复杂度为O(N^2)。
O(N2)的时间复杂度是一个比较糟糕的结果，尤其在数据量很大的情况下。所以冒泡排序通常不会用于实际应用。

代码改进
针对有的列表有部分数据已经有序，不需要在进行判断，则对冒泡排序进行改进。

def optsortBubble(alist):
    al=len(alist)-1
    exchange=True
    while al>0 and exchange:
        exchange=False
        for i in range(al):
            if alist[i]>alist[i+1]:
                exchange = True
                alist[i],alist[i+1]= alist[i+1],alist[i]
        al-=1
    return alist

if __name__ == "__main__":
    res= optsortBubble([2,3,5,8,2,6,4])
    print(res)

小结：
冒泡排序属于最经典的排序算法，由于其直观性，很容易被应试者作为第一个解决办法想到。
由于每次交换，只需要临时存储一个数字，所以空间复杂度为O(1)。
最好情况是数据是已经有序的，这样遍历一次就可以结束，最好时间复杂度为O(n)。
最坏情况是数据是逆序，这样每次遍历都需要交换一次，最坏时间复杂度为 [公式] 。
由于出现两个相同数字不会导致交换，所以相同数字相对位置不变，冒泡排序是稳定的排序算法。

4.2 选择排序

选择排序是在冒泡排序的基础上进行改进。每次遍历列表只进行一次交换。要实现这一点，选择排序每次遍历寻找最大值，并在遍历完成后将它放在正确的位置上。

算法步骤
1、首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
2、再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
3、重复第二步，直到所有元素均排序完毕。

# -*- coding:utf-8 -*-
"""
选择排序算法：多次遍历列表，一轮遍历将最大值放在列表最后面。并且每次缩小遍历的列表的大小。

"""
def optselectBubble(alist):
    al=len(alist)
    tempt=0
    while al>1:
        for i in range(0,al):
            if alist[i]>alist[tempt]:
                tempt=i
        alist[i],alist[tempt]= alist[tempt],alist[i]
        print(alist)
        al=al-1
        tempt=0
    return alist

if __name__ == "__main__":
    res= optselectBubble([2,5,1,3,8,2,6,4])
    print("最终结果：")
    print(res)```

通过每次记录最小值：

```python
#通过每次记录最小数值的索引
def select_sort(L):
    n=len(L)
    if n==0:
        return None
    for i in range(n-1):
        minindex=i
        for j in range(i+1,n):
            if L[j]<L[minindex]:
                minindex=j
        L[minindex],L[i]= L[i],L[minindex]
    return L



if __name__ == '__main__':
    L = [3,2, 6]
    res = select_sort(L)
    print(res)

java实现：

时间复杂度
最优时间复杂度：O(n) （升序排列，序列已经处于升序状态）
最坏时间复杂度：O(n^2)
稳定性：稳定
在第一趟排序中，插入排序最多比较一次，第二趟最多比较两次，依次类推，最后一趟最多比较N-1次。因此有：1+2+3+…+N-1 = NN(N-1)/2
因为在每趟排序发现插入点之前，平均来说，只有全体数据项的一半进行比较，我们除以2得到：NN(N-1)/4
复制的次数大致等于比较的次数，然而，一次复制与一次比较的时间消耗不同，所以相对于随机数据，这个算法比冒泡排序快一倍，比选择排序略快。
与冒泡排序、选择排序一样，插入排序的时间复杂度仍然为O(N^2)，这三者被称为简单排序或者基本排序，三者都是稳定的排序算法。
如果待排序数组基本有序时，插入排序的效率会更高

改进思路
有一种比较常见的改进思路，就是每次在循环的时候，不仅找到最小的元素，放到数组最左边，也找到最大的元素，放到数组最右边。这样可以减少一半的循环次数。

def Selection_Sort_Opt(array):
    for i in range(len(array)-1):
        min_index = i
        max_index = len(array) - 1 - i
        for j in range(i+1, len(array) - i - 1):
            if array[j] < array[min_index]:
                min_index = j
            if array[j] > array[max_index]:
                max_index = j
        if min_index != i:
            tmp = array[i] 
            array[i] = array[min_index]
            array[min_index] = tmp
        if max_index != len(array) - i - 1:
            tmp = array[len(array) - i - 1] 
            array[len(array) - i - 1] = array[max_index]
            array[max_index] = tmp

4.3 插入排序 (Insertion Sort)

插入排序的算法思想也很直观：每次从待排序数组中取一个元素，在已排序数组中找到其应该在的位置插入，后面的元素则依次向后移动一位。
算法步骤
1、第一个元素默认已有序；
2、取下一个待比较元素，从已排序的序列中从后往前扫描；
3、如果当前已排序序列元素 > 当前待比较元素，则已排序序列元素向后移动一个位置；
4、重复直到将待比较元素插入到已排序序列中；
5、重复上述操作直到所有元素有序。

def insert_sort(arr):
    for i in range(1,len(arr)):
        tempt=arr[i]
        j=i-1
        while j>=0 and tempt<arr[j]:
            #向后平移
            arr[j+1]=arr[j]
            j-=1
        arr[j+1]=tempt

if __name__=="__main__":
    arr=[2,4,5,6,7,3,4,6]
    insert_sort(arr)
    print(arr)

输出结果：
[2, 3, 4, 4, 5, 6, 6, 7]

用未排序序列第一个元素，从已排序序列尾部到起始位置方向开始比较，也就是插入元素和已排序最大元素开始比较，一直找到比它小的元素位置后插入。


def insertSort(array):
    n=len(array)
    for i in range(n):
        for j in range(1,i+1):
            if array[j]>array[j-1]:
                array[j], array[j - 1]=array[j-1], array[j]


if __name__ == "__main__":
    array = [3, 2, 1,8,55,43,2,1,0]
    insertSort(array)
    print(array)

输出：[55, 43, 8, 3, 2, 2, 1, 1, 0]

4.4 希尔排序

希尔排序是插入排序的一种又称“缩小增量排序”，是直接插入排序算法的一种更高效的改进版本。希尔排序是非稳定排序算法。
希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。
希尔排序的核心是对步长的理解，步长是进行相对比较的两个元素之间的距离，随着步长的减小，相对元素的大小会逐步区分出来并向两端聚拢，当步长为1的时候，就完成最后一次比较，那么序列顺序就出来了。

def shell_sort(items):
    """
    希尔排序
    :param items:
    :return:
    """
    n = len(items)
    step = n // 3
    print("++++1++++")
    print("step:" + str(step))
    while step > 0:
        for cur in range(step, n):
            i = cur
            while i >= step and items[i-step] > items[i]:
                print(i,i-step)
                items[i - step], items[i] = items[i], items[i-step]
                i -= step
        step = step // 3
        print("++++2++++")
        print("step:"+str(step))



if __name__ == "__main__":
    arr = [2, 5, 8, 0, 1, 4, 2, 7, 10, 67, 34]
    shell_sort(arr)
    n=len(arr)
    print("\n排序后:")
    for i in range(n):
        print(arr[i], end=",")

python代码演示，是从step到n,然后从后面跟前面比较

def shell_sort(items):
    """
    希尔排序
    :param items:
    :return:
    """
    n = len(items)
    step = n // 3
    print("++++1++++")
    print("step:" + str(step))
    while step > 0:
        for cur in range(step, n):
            i = cur
            print("i:"+str(i))
            while i >= step and items[i-step] > items[i]:
                print(i,i-step)
                items[i - step], items[i] = items[i], items[i-step]
                i -= step
        step = step // 3
        print("++++2++++")
        print("step:"+str(step))



if __name__ == "__main__":
    arr = [2, 5, 8, 0, 1, 4, 2, 7, 10, 67, 34,66,334,12,213,32,454,67,23,12,345]
    shell_sort(arr)
    n=len(arr)
    print("\n排序后:")
    print("n:"+str(n))
    for i in range(n):
        print(arr[i], end=",")

希尔排序可以理解成插入排序的优化版本。希尔排序是先将任意间隔为N的元素有序，刚开始可以是N=n/2，接着让N=N/2，让N一直缩小，当N=1,时，此时序列间隔为1有序。

步骤：
1、初始间隔N=数组长度/2
2、对间隔为N的分组进行插入排序，直至有序
3、缩小N值，N=N/2；
4、重复2、3步骤，直至间隔N=1

"""
希尔排序
希尔排序可以理解成插入排序的优化版本。希尔排序是先将任意间隔为N的元素有序，刚开始可以是N=n/2，接着让N=N/2，让N一直缩小，当N=1,时，此时序列间隔为1有序。
"""


def shellSortCore(arr):
    gap = len(arr) // 2
    while gap:
        print(gap)
        for i in range(gap, len(arr)):
            m = arr[i]
            for j in range(i - gap, -1,-1):  #j到0
                if m < arr[j]:
                    arr[j], arr[j + gap] = arr[j + gap], arr[j]
        print(arr)
        gap //= 2



if __name__ == "__main__":
    array = [3, 2, 1, 4, 5, 3, 2, 55, 4645, 3, 2, 32, 7, 89, 9, 10]
    shellSortCore(array)
    print(array)

输出：
[1, 2, 2, 2, 3, 3, 3, 4, 5, 7, 9, 10, 32, 55, 89, 4645]

4.5 快速排序

快速排序采用分治策略。

快速排序是一种交换排序。

基本思想：通过一趟排序将要排序的数据分割成独立的两部分：分割点左边都是比它小的数，右边都是比它大的数。

然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

详细的图解往往比大堆的文字更有说明力，所以直接上图：

public int division(int[] list, int left, int right) {
    // 以最左边的数(left)为基准
    int base = list[left];
    while (left < right) {
        // 从序列右端开始，向左遍历，直到找到小于base的数
        while (left < right && list[right] >= base)
            right--;
        // 找到了比base小的元素，将这个元素放到最左边的位置
        list[left] = list[right];

        // 从序列左端开始，向右遍历，直到找到大于base的数
        while (left < right && list[left] <= base)
            left++;
        // 找到了比base大的元素，将这个元素放到最右边的位置
        list[right] = list[left];
    }

    // 最后将base放到left位置。此时，left位置的左侧数值应该都比left小；
    // 而left位置的右侧数值应该都比left大。
    list[left] = base;
    return left;
}

private void quickSort(int[] list, int left, int right){

    // 左下标一定小于右下标，否则就越界了
    if (left < right) {
        // 对数组进行分割，取出下次分割的基准标号
        int base = division(list, left, right);

        System.out.format("base = %d:\t", list[base]);
        printPart(list, left, right);

        // 对“基准标号“左侧的一组数值进行递归的切割，以至于将这些数值完整的排序
        quickSort(list, left, base - 1);

        // 对“基准标号“右侧的一组数值进行递归的切割，以至于将这些数值完整的排序
        quickSort(list, base + 1, right);
    }
}

python实现

def partition(arr,low,high): 
    i = ( low-1 )         # 最小元素索引
    pivot = arr[high]      #最末尾的数
  
    for j in range(low , high): 
  
        # 当前元素小于或等于 pivot 
        if   arr[j] <= pivot: 
            i = i+1 
            arr[i],arr[j] = arr[j],arr[i] 
  
    arr[i+1],arr[high] = arr[high],arr[i+1] 
    return i+1
  

def quickSort(arr,low,high): 
    if low < high: 
  
        pi = partition(arr,low,high) 
  
        quickSort(arr, low, pi-1) 
        quickSort(arr, pi+1, high) 
  
arr = [10, 7, 8, 9, 1, 5] 
n = len(arr) 
quickSort(arr,0,n-1) 
print ("排序后的数组:") 
for i in range(n): 
    print ("%d" %arr[i],end=",")

下面以数列a={30,40,60,10,20,50}为例，演示它的快速排序过程(如下图)。

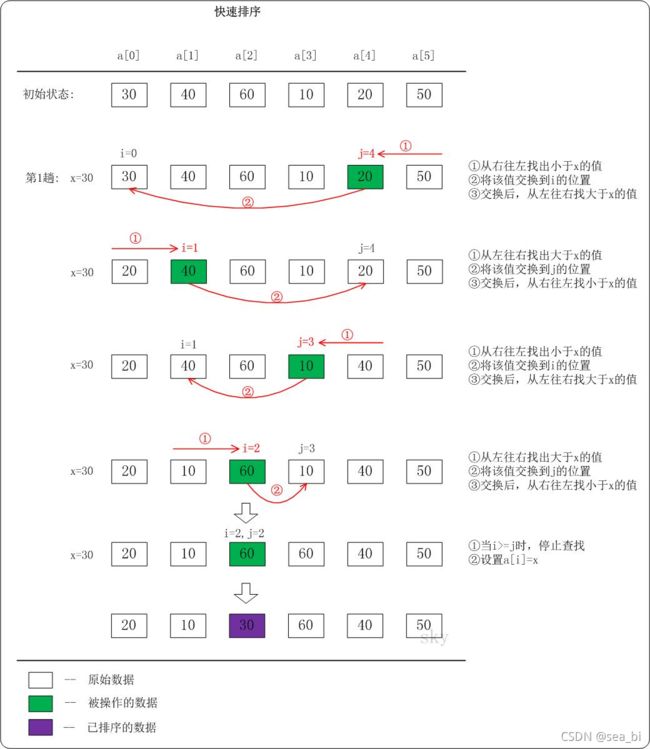
上图只是给出了第1趟快速排序的流程。在第1趟中，设置x=a[i]，即x=30。

(01) 从"右 --> 左"查找小于x的数：找到满足条件的数a[j]=20，此时j=4；然后将a[j]赋值a[i]，此时i=0；接着从左往右遍历。

(02) 从"左 --> 右"查找大于x的数：找到满足条件的数a[i]=40，此时i=1；然后将a[i]赋值a[j]，此时j=4；接着从右往左遍历。

(03) 从"右 --> 左"查找小于x的数：找到满足条件的数a[j]=10，此时j=3；然后将a[j]赋值a[i]，此时i=1；接着从左往右遍历。

(04) 从"左 --> 右"查找大于x的数：找到满足条件的数a[i]=60，此时i=2；然后将a[i]赋值a[j]，此时j=3；接着从右往左遍历。

(05) 从"右 --> 左"查找小于x的数：没有找到满足条件的数。当i>=j时，停止查找；然后将x赋值给a[i]。此趟遍历结束！

按照同样的方法，对子数列进行递归遍历。最后得到有序数组！

def quick_sort(lists,i,j):
    if i >= j:
        return list
    pivot = lists[i]
    low = i
    high = j
    while i < j:
        while i < j and lists[j] >= pivot:
            j -= 1
        lists[i]=lists[j]
        while i < j and lists[i] <=pivot:
            i += 1
        lists[j]=lists[i]
    lists[j] = pivot
    quick_sort(lists,low,i-1)
    quick_sort(lists,i+1,high)
    return lists

if __name__=="__main__":
    lists=[30,24,5,58,18,36,12,42,39]
    print("排序前的序列为：")
    for i in lists:
        print(i,end =" ")
    print("\n排序后的序列为：")
    for i in quick_sort(lists,0,len(lists)-1):
        print(i,end=" ")

好了今天就学到这里。

4.6 归并排序（Merge sort）

归并排序是经典的分而治之的一种应用。
分治法在每层递归时有三个步骤：
1、分解：将待排序的 n 个元素分成各包含 n/2 个元素的子序列
2、解决：使用归并排序递归排序两个子序列
3、合并：合并两个已经排序的子序列以产生已排序的答案
考虑我们排序这个数组：[10,23,51,18,4,31,13,5] ，我们递归地将数组进行分解

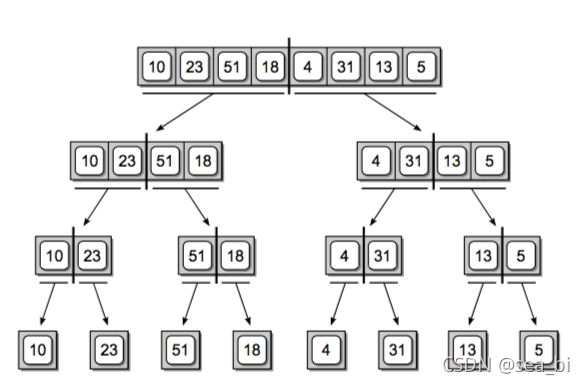
当数组被完全分隔成只有单个元素的数组时，我们需要把它们合并回去，每次两两合并成一个有序的序列。

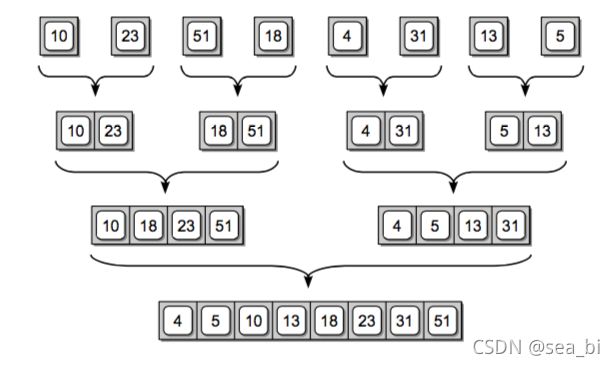
归并排序主要通过先递归地将数组分为两个部分，排序后，再将元素合并到一起。

所以归根结底归并排序就是两部分组成：拆分+合并！

用递归代码来描述这个问题：

def merge_sort(seq):
    if len(seq) <= 1:   # 只有一个元素是递归出口
        return seq
    else:
        mid = int(len(seq)/2)
        left_half = merge_sort(seq[:mid])
        right_half = merge_sort(seq[mid:])

        # 合并两个有序的数组
        new_seq = merge_sorted_list(left_half, right_half)
        return new_seq

#合并
 def merge_sorted_list(sorted_a, sorted_b):
    """ 合并两个有序序列，返回一个新的有序序列

    :param sorted_a:
    :param sorted_b:
    """
    length_a, length_b = len(sorted_a), len(sorted_b)
    a = b = 0
    new_sorted_seq = list()

    while a < length_a and b < length_b:
        if sorted_a[a] < sorted_b[b]:
            new_sorted_seq.append(sorted_a[a])
            a += 1
        else:
            new_sorted_seq.append(sorted_b[b])
            b += 1

    # 最后别忘记把多余的都放到有序数组里
    if a < length_a:
        new_sorted_seq.extend(sorted_a[a:])
    else:
        new_sorted_seq.extend(sorted_b[b:])

    return new_sorted_seq

归并排序采用分治思想，把待排序序列分成N个子序列，子序列排序后，合并两个子序列实现排序。
步骤：

合并步骤：

1、申请临时存储空间，大小为两个待排序数组A，B大小之和；
2、利用a,b两个指针，分别指向A和B数组的头部；
3、比较a，b指针对应数字大小，选择小的数字放入临时存储空间，并且对应指针后移一位；
4、重复直到某一指针到达了对应数组尾部；
5、将剩余所有元素放入临时存储空间。

"""
归并排序
归并排序采用分治思想，把待排序序列分成N个子序列，子序列排序后，合并两个子序列实现排序
"""
def Merge_Sort(array):
    if len(array) < 2:
        return array
    mid = len(array)//2
    # 左边
    left = Merge_Sort(array[:mid])
    # 右边
    right = Merge_Sort(array[mid:])
    # 合并
    i, j = 0, 0
    res = []
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            res.append(left[i])
            i += 1
        else:
            res.append(right[j])
            j += 1
    return res + left[i:] + right[j:]

if __name__=="__main__":
    array=[3,2,1,5,5,7,8,3,23,42,42,3,2,1]
    res=Merge_Sort(array)
    print(res)

输出：
[1, 1, 2, 2, 3, 3, 3, 5, 5, 7, 8, 23, 42, 42]

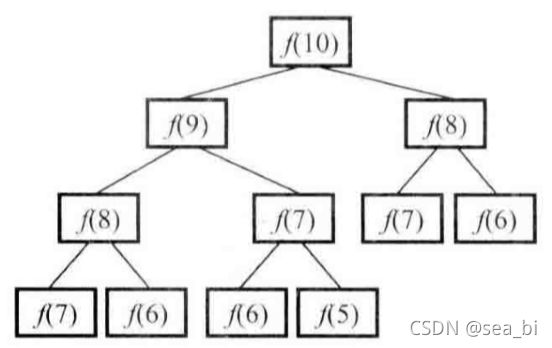
4.7 堆排序（***）

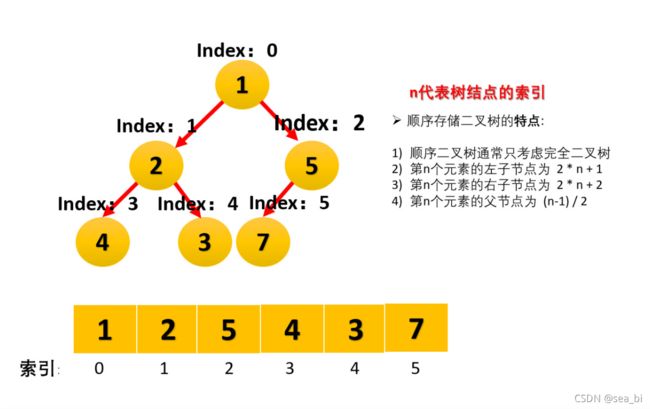
堆排序（Heap Sort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，
每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；
或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：

代码实现思路：
步骤一构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

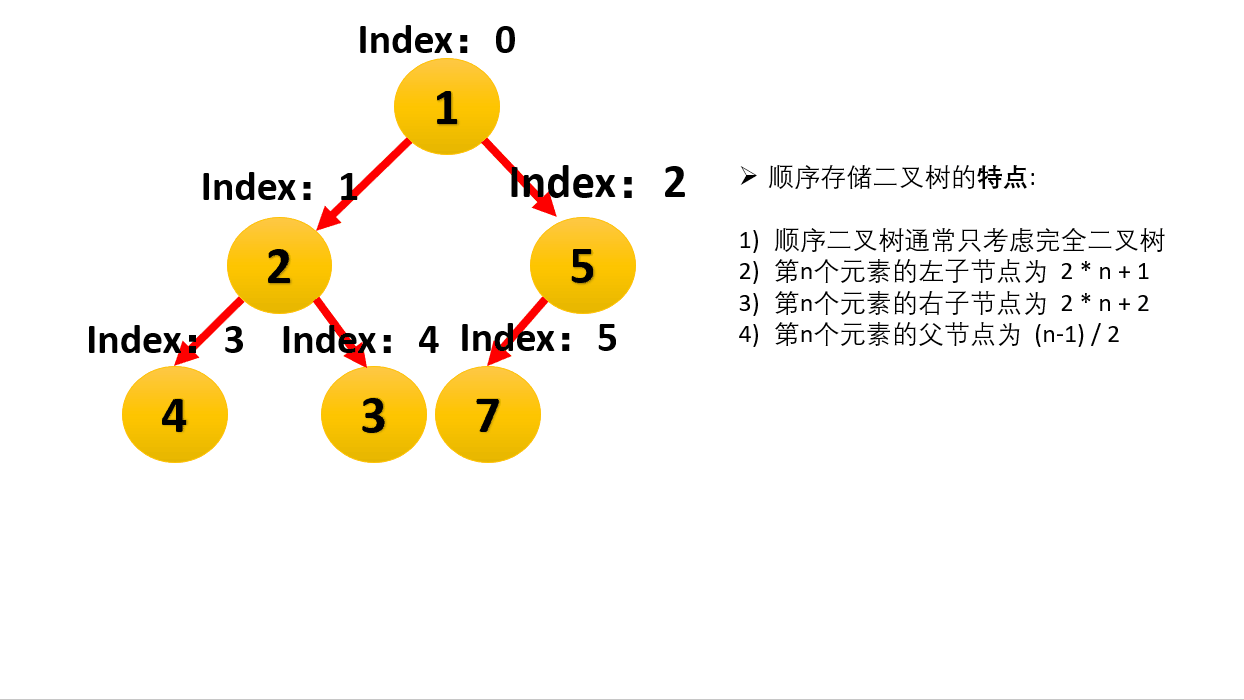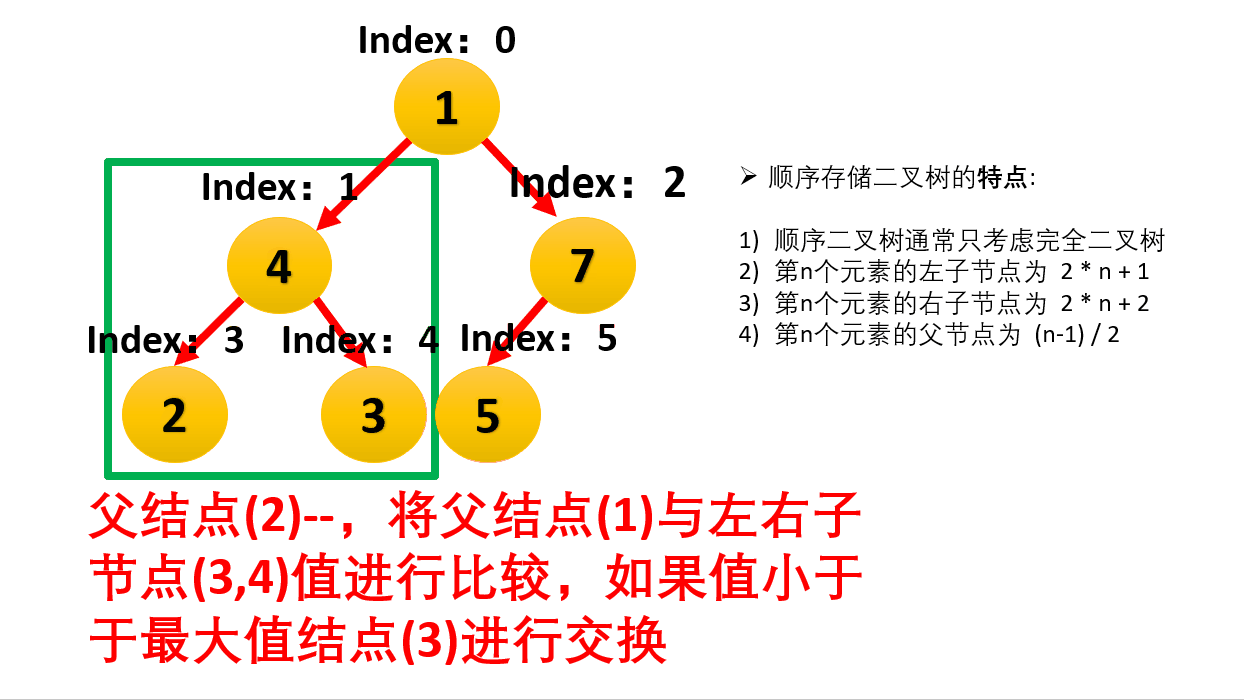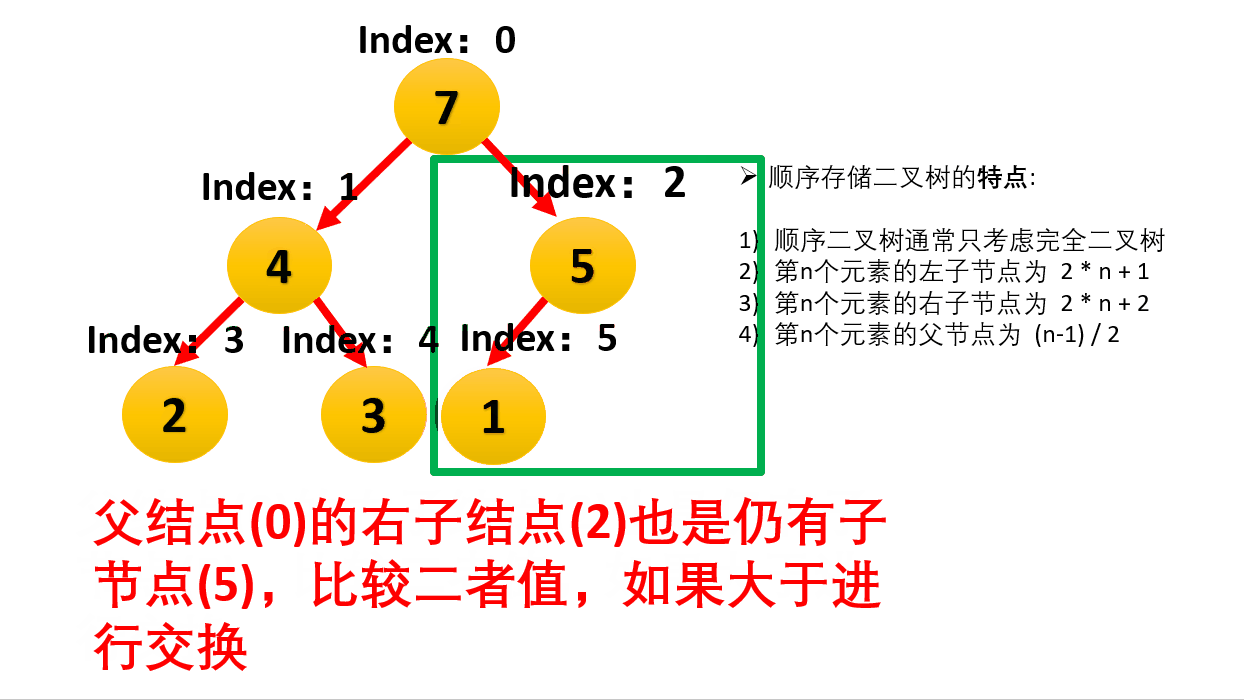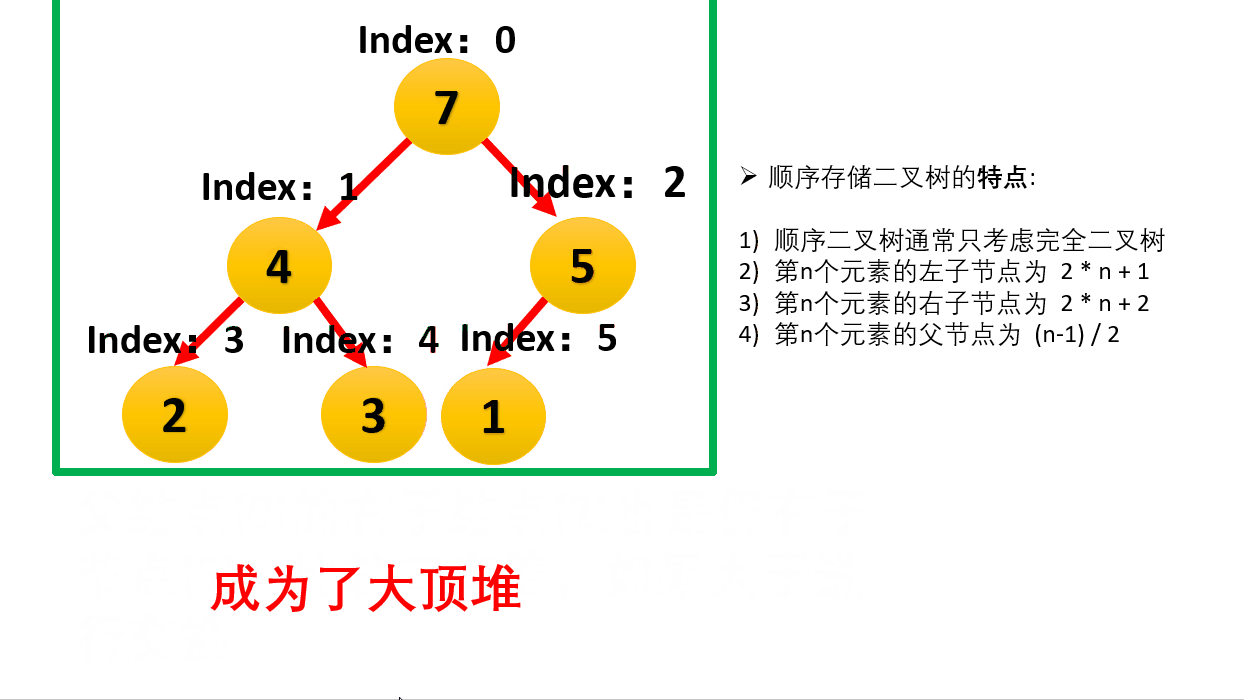
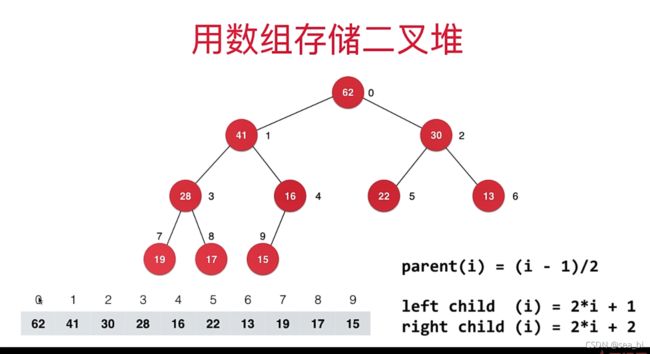
用数组存储二叉堆，堆的顶点下标可以从0开始也可以从1开始。
看上面图中，以self为参照物，self下标的变量为i：
从0开始：
parent(i) = (i - 1) / 2;
leftChild(i) = 2 * i + 1；
rightChild(i) = leftChild(i) + 1 = 2 * i + 2;

如果是堆顶下标从1开始：
parent(i) = i / 2;
leftChild = 2 * i;
rightChild = 2 * i + 1;

4.7.1 最大二叉堆

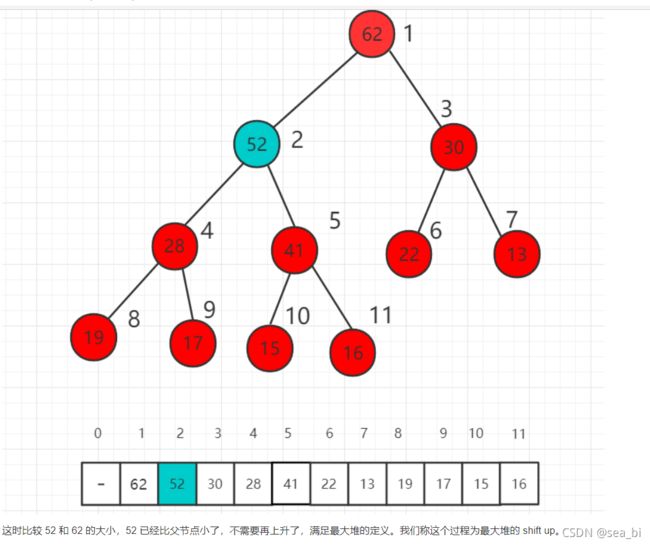
最大堆的 shift up
假设我们对下面的最大堆新加入一个元素52，放在数组的最后一位，52大于父节点16，此时不满足堆的定义，需要进行调整。

# 最大二叉堆
class BinaryHeap(object):
    # 创建一个新的，空的二叉堆。
    def __init__(self):
        self.item_list = [0]  # 第0项元素代表堆中存放的实际元素的个数

    # 向堆添加一个新项。
    def insert(self, new_item):
        self.item_list.append(new_item)
        self.item_list[0] += 1  # 记录元素个数的增加
        self.upward_adjust(self.item_list[0])  # 向上调整

    # 向上调整:堆的 shift up
    def upward_adjust(self, index):
        while index // 2 > 0:  # 父节点存在
            if self.item_list[index] > self.item_list[index // 2]:  # 如果当前节点比父亲节点更大，则交换
                #交换节点
                temp = self.item_list[index]
                self.item_list[index] = self.item_list[index // 2]
                self.item_list[index // 2] = temp
                index = index // 2  # 继续调整
            else:  # 如果当前节点不比父节点小
                break  # 停止调整

为了通过对一个数列进行堆排序，采用向下调整:堆的 shift down：

# 最小二叉堆
class BinaryHeap(object):
    # 创建一个新的，空的二叉堆。
    def __init__(self):
        self.item_list = [0]  # 第0项元素代表堆中存放的实际元素的个数

    # 返回具有最小键值的项，并将项留在堆中。
    def get_min(self):
        if self.item_list[0] > 0:  # 不为空，返回堆顶
            return self.item_list[1]
        else:
            return None

    # 返回具有最小键值的项，从堆中删除该项。
    def pop_min(self):
        if self.item_list[0] == 0:  # 如果为空，返回None
            return None
        else:
            top_min = self.item_list[1]  # 将堆顶元素
            self.item_list[1] = self.item_list[self.item_list[0]]  # 将最后一个元素移动到堆顶
            self.item_list[0] -= 1
            self.downward_adjust(1)  # 向下调整
            return top_min

    # 向下调整:堆的 shift down
    def downward_adjust(self, index):
        while 2 * index <= self.item_list[0]:  # 子节点存在
            if 2 * index + 1 <= self.item_list[0]:  # 左右子节点都存在
                if self.item_list[2 * index] > self.item_list[2 * index + 1]:  # 左子节点更大
                    if self.item_list[index] < self.item_list[2 * index]:  # 根节点比左子节点更小，交换
                        temp = self.item_list[index]
                        self.item_list[index] = self.item_list[2 * index]
                        self.item_list[2 * index] = temp
                        index = 2 * index  # 继续调整
                    else:  # 没有比子节点更大，停止调整
                        break
                else:  # 右子节点更大
                    if self.item_list[index] < self.item_list[2 * index + 1]:  # 比右子节点更大，交换
                        temp = self.item_list[index]
                        self.item_list[index] = self.item_list[2 * index + 1]
                        self.item_list[2 * index + 1] = temp
                        index = 2 * index + 1  # 继续调整
                    else:  # 没有比子节点更大，停止调整
                        break
            else:  # 只存在左节点
                if self.item_list[index] < self.item_list[2 * index]:  # 根节点比左子节点更小，交换
                    temp = self.item_list[index]
                    self.item_list[index] = self.item_list[2 * index]
                    self.item_list[2 * index] = temp
                else:  # 根节点比子节点更大，停止调整
                    break

    # 判断是否为空
    def isEmpty(self):
        return 0 == self.item_list[0]

    # 返回堆中的项数
    def size(self):
        return self.item_list[0]

    # 从列表构建一个新的堆。覆盖掉当前的堆
    def build_heap(self, input_list):
        self.item_list = [0] + input_list
        self.item_list[0] = len(input_list)
        for index in range(self.item_list[0] // 2, 0, -1):  # 从最后一个有叶节点的元素起逐个向下调整
            self.downward_adjust(index)
            
def main():
    bh = BinaryHeap()
    L=[ 12, 11, 13, 5, 6, 7]
    bh.build_heap(L)

    for i in range(len(L)):
        print(bh.pop_min(),end=",")


if __name__ == "__main__":
    main()

输出结果：
13,12,11,7,6,5

最小二叉堆也是类似原理构成。

4.7.2 优化堆排序

把最后一个元素和根元素交换，然后取出最后一个元素到一个特定的list中。然后把剩下的数列再次调整为一个大根堆

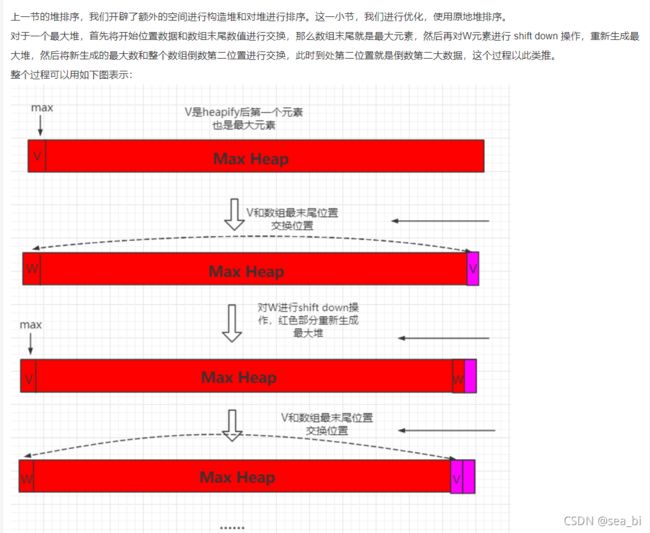
我们发现，对于最大堆来说，根节点的元素总是最大的，因此，如果每次都把根节点的元素和最后的元素互换位置，然后再把堆的跟节点进行一次shift down，那么最后一个元素就是整个数组的最大值，基于这个思想，如果不断进行这样的操作，利用堆的性质，就可以让一个数组最终从大到小排序。

# 最大二叉堆
class BinaryHeap(object):
    # 创建一个新的，空的二叉堆。
    def __init__(self):
        self.item_list = [0]  # 第0项元素代表堆中存放的实际元素的个数

    # 向堆添加一个新项。
    def insert(self, new_item):
        self.item_list.append(new_item)
        self.item_list[0] += 1  # 记录元素个数的增加
        self.upward_adjust(self.item_list[0])  # 向上调整

    # 向上调整:堆的 shift up
    def upward_adjust(self, index):
        while index // 2 > 0:  # 父节点存在
            if self.item_list[index] > self.item_list[index // 2]:  # 如果当前节点比父亲节点更大，则交换
                #交换节点
                temp = self.item_list[index]
                self.item_list[index] = self.item_list[index // 2]
                self.item_list[index // 2] = temp
                index = index // 2  # 继续调整
            else:  # 如果当前节点不比父节点小
                break  # 停止调整

    # 返回具有最大键值的项，并将项留在堆中。
    def get_max(self):
        if self.item_list[0] > 0:  # 不为空，返回堆顶
            return self.item_list[1]
        else:
            return None

    # 返回具有最最大键值的项，从堆中删除该项。
    def pop_max(self):
        if self.item_list[0] == 0:  # 如果为空，返回None
            return None
        else:
            top_max = self.item_list[1]  # 将堆顶元素
            self.item_list[1] = self.item_list[self.item_list[0]]  # 将最后一个元素移动到堆顶
            #返回最后的项，重新下沉，并将最大值去除
            self.item_list[0] -= 1
            self.downward_adjust(1)  # 向下调整
            return top_max

    # 向下调整:堆的 shift down
    def downward_adjust(self, index):
        while 2 * index <= self.item_list[0]:  # 左子节点存在
            if 2 * index + 1 <= self.item_list[0]:  # 右子节点都存在
                if self.item_list[2 * index] > self.item_list[2 * index + 1]:  # 左子节点更大
                    if self.item_list[index] < self.item_list[2 * index]:  # 根节点比左子节点更小，交换
                        temp = self.item_list[index]
                        self.item_list[index] = self.item_list[2 * index]
                        self.item_list[2 * index] = temp
                        index = 2 * index  # 继续调整
                    else:  # 没有比子节点更大，停止调整
                        break
                else:  # 右子节点更大
                    if self.item_list[index] < self.item_list[2 * index + 1]:  # 比右子节点更大，交换
                        temp = self.item_list[index]
                        self.item_list[index] = self.item_list[2 * index + 1]
                        self.item_list[2 * index + 1] = temp
                        index = 2 * index + 1  # 继续调整
                    else:  # 没有比子节点更大，停止调整
                        break
            else:  # 只存在左节点
                if self.item_list[index] < self.item_list[2 * index]:  # 根节点比左子节点更小，交换
                    temp = self.item_list[index]
                    self.item_list[index] = self.item_list[2 * index]
                    self.item_list[2 * index] = temp
                else:  # 根节点比子节点更大，停止调整
                    break

    # 判断是否为空
    def isEmpty(self):
        return 0 == self.item_list[0]

    # 返回堆中的项数
    def size(self):
        return self.item_list[0]

    # 从列表构建一个新的堆。覆盖掉当前的堆
    def build_heap(self, input_list):
        self.item_list = [0] + input_list
        self.item_list[0] = len(input_list)
        for index in range(self.item_list[0] // 2, 0, -1):  # 从最后一个有叶节点的元素起逐个向下调整
            self.downward_adjust(index)
            print(self.item_list)


    #原地堆排序
    def heapSort(self,arr):
        if self.item_list[0] == 0:  # 如果为空，返回None
            return None
        else:
            top_max = self.item_list[1]  # 将堆顶元素
            self.item_list.append(arr)
            self.item_list[0] = len(self.item_list)-1
            self.item_list[1] = self.item_list[self.item_list[0]]  # 将最后一个元素移动到堆顶
            self.item_list[-1]=top_max
            # 返回最后的项，重新下沉
            self.downward_adjust(1)  # 向下调整
            self.upward_adjust(self.item_list[0])#向上调整
            return self.item_list[1:]


def main():
    bh = BinaryHeap()
    bh.build_heap([1,8,2,3,5])

    heapsort=bh.heapSort(22)
    print(heapsort)


if __name__ == "__main__":
    main()

4.7.3 Python 堆排序（菜鸟教程）

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。


def heapify(arr, n, i):
    largest = i
    l = 2 * i + 1     # left = 2*i + 1
    r = 2 * i + 2     # right = 2*i + 2

    if l < n and arr[i] < arr[l]:
        largest = l

    if r < n and arr[largest] < arr[r]:
        largest = r

    if largest != i:
        arr[i] ,arr[largest] = arr[largest] ,arr[i]  # 交换

        heapify(arr, n, largest)

def heapSort(arr):
    n = len(arr)

    # Build a maxheap.
    for i in range(n, -1, -1):
        heapify(arr, n, i)

        # 一个个交换元素
    for i in range( n -1, 0, -1):
        arr[i], arr[0] = arr[0], arr[i]   # 交换
        heapify(arr, i, 0)



if __name__=="__main__":
    arr = [12, 11, 13, 5, 6, 7]
    heapSort(arr)
    n = len(arr)
    print("排序后")
    for i in range(n):
        print("%d" % arr[i],end=",")

输出：
5,6,7,11,12,13

4.8 计数排序

计数排序（Counting Sort）不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。
排序步骤：

找出待排序的数组中最大和最小的元素；
1、统计数组中每个值为i的元素出现的次数，存入数组C的第i项；
2、对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；
3、反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

def countSort(alist,k):
    n=len(alist)
    b=[0 for i in range(n)]
    c=[0 for i in range(k+1)]
    for i in alist:
        c[i]+=1
    for i in range(1,len(c)):
        c[i]=c[i-1]+c[i]
    for i in alist:
        b[c[i]-1]=i
        c[i]-=1
    return b

if __name__=="__main__":
    arr = [1, 4, 6, 7, 5, 4]
    ans =countSort(arr,100)
    for i in ans:
        print(i,end=",")

输出结果：
1,4,4,5,6,7,

4.9 桶排序(Bucket Sort)

实现：

# coding:utf-8

# !/usr/bin/env python

# Time: 2018/8/9 9:31

# Author: sty

# File: bucket_sort.py



def bucket_sort(arr):
    """桶排序"""
    min_num = min(arr)
    max_num = max(arr)
    # 桶的大小
    bucket_range = (max_num - min_num) / len(arr)
    # 桶数组
    count_list = [[] for i in range(len(arr) + 1)]
    # 向桶数组填数
    for i in arr:
        count_list[int((i - min_num) // bucket_range)].append(i)
    arr.clear()
    # 回填，这里桶内部排序直接调用了sorted
    for i in count_list:
        for j in sorted(i):
            arr.append(j)
    return arr


if __name__ == '__main__':
    array = [1,5,3,2,4,6,11]
    n = len(array)
    array = bucket_sort(array)
    print(array)

输出结果：
[1, 2, 3, 4, 5, 6, 11]

4.10 基数排序（Radix Sort）

算法思想
基数排序的原理相对于其它方法来说，比较新颖有趣。它将数字按照位数(个十百)切分，然后按每个位数分别比较。对于数字长度不一致情况，将高位（前面）补零。该方法为最低位优先法LSD(Least sgnificant digital)。

5 链表(LinkList)

链表(LinkList)
数据存储在“节点(Node)”中，
节点包含的内容：数据和下一个节点的指针
链表额增删改查的时间复杂度全部是O(n)级别，但是在链表头的操作的时间复杂度是O(1)的
优点：真正的动态，不需要考虑容量的问题
缺点：丧失了随机访问的能力，因为每一个节点通过next指针穿插起来，不是连续存储的

和数组对比
数组最好用于索引有语意的情况。例如scores[2]
是线性结构
数组最大的优点：支持快速查询

链表不适合用于索引有语意的情况
不是线性结构
链表最大的优点：真正的动态，不浪费存储空间

5.1 单链表

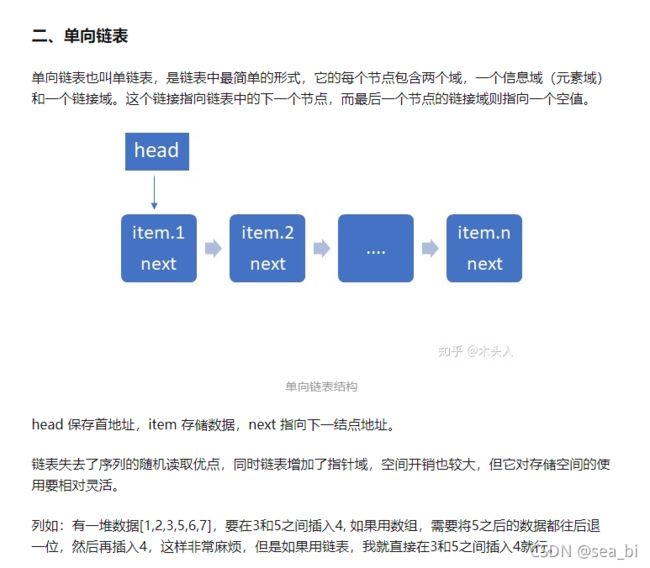
表元素域data用来存放具体的数据。
链接域next用来存放下一个节点的位置

定义节点：

class Node(object):
    """单链表的结点"""

    def __init__(self, item):
        # item存放数据元素
        self.item = item
        # next是下一个节点的标识
        self.next = None

定义链表：

#2. 定义链表
class SingleLinkList(object):
    """单链表"""

    def __init__(self):
        self._head = None

创建链表：

#创建链表
if __name__=="__main__":
    link_list=SingleLinkList()
    #创建节点
    node1=Node(1)
    node2=Node(2)
    
     # 将结点添加到链表
    link_list._head = node1
    # 将第一个结点的next指针指向下一结点
    node1.next = node2

    # 访问链表
    print(link_list._head.item)  # 访问第一个结点数据
    print(link_list._head.next.item)  # 访问第二个结点数据

class Node(object):
    """单链表的结点"""

    def __init__(self, item):
        # item存放数据元素
        self.item = item
        # next是下一个节点的标识
        self.next = None


class SingleLinkList(object):
    """单链表"""

    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def length(self):
        """链表长度"""
        # 初始指针指向head
        cur = self._head
        count = 0
        # 指针指向None 表示到达尾部
        while cur is not None:
            count += 1
            # 指针下移
            cur = cur.next
        return count

    def items(self):
        """遍历链表"""
        # 获取head指针
        cur = self._head
        # 循环遍历
        while cur is not None:
            # 返回生成器
            yield cur.item
            # 指针下移
            cur = cur.next

    def add(self, item):
        """向链表头部添加元素"""
        node = Node(item)
        # 新结点指针指向原头部结点
        node.next = self._head
        # 头部结点指针修改为新结点
        self._head = node

    def append(self, item):
        """尾部添加元素"""
        node = Node(item)
        # 先判断是否为空链表
        if self.is_empty():
            # 空链表，_head 指向新结点
            self._head = node
        else:
            # 不是空链表，则找到尾部，将尾部next结点指向新结点
            cur = self._head
            while cur.next is not None:
                cur = cur.next
            cur.next = node

    def insert(self, index, item):
        """指定位置插入元素"""
        # 指定位置在第一个元素之前，在头部插入
        if index <= 0:
            self.add(item)
        # 指定位置超过尾部，在尾部插入
        elif index > (self.length() - 1):
            self.append(item)
        else:
            # 创建元素结点
            node = Node(item)
            cur = self._head
            # 循环到需要插入的位置
            for i in range(index - 1):
                cur = cur.next

            node.next = cur.next
            cur.next = node

    def remove(self, item):
        """删除节点"""
        cur = self._head
        pre = None
        while cur is not None:
            # 找到指定元素
            if cur.item == item:
                # 如果第一个就是删除的节点
                if not pre:
                    # 将头指针指向头节点的后一个节点
                    self._head = cur.next
                else:
                    # 将删除位置前一个节点的next指向删除位置的后一个节点
                    pre.next = cur.next
                return True
            else:
                # 继续按链表后移节点
                pre = cur
                cur = cur.next

    def find(self, item):
        """查找元素是否存在"""
        return item in self.items()

    def getIndex(self, data):
        if self.is_empty():
            print("error : out of index")
            return None
        cur = self._head
        index = 0
        while cur is not None:
            # 返回生成器
            if cur.item == data:
                return index
            # 指针下移
            index += 1
            cur = cur.next
        return None

    def show(self):
        if self.is_empty():
            print("空链表")
            return None
        cur = self._head
        while cur is not None:
            print(cur.item, end="-->")
            cur = cur.next
        print("\n")

    def deleteIdex(self, index):
        if index == 0:
            self._head = self._head.next
            return
        elif index > (self.length() - 1):
            return
        j = 0
        node = self._head
        pre = self._head
        while node.next and j < index:
            pre = node
            node = node.next
            j += 1
        if j == index:
            pre.next = node.next


if __name__ == '__main__':
    link_list = SingleLinkList()
    # 向链表尾部添加数据
    for i in range(5):
        link_list.append(i)
    print("向链表尾部添加数据后，链表的结构:")
    print(list(link_list.items()))
    link_list.show()
    # 向头部添加数据
    link_list.add(6)
    # 遍历链表数据
    print("遍历链表数据:")
    for i in link_list.items():
        print(i, end='\t')
    # 链表数据插入数据
    link_list.insert(3, 9)
    print("\n链表数据插入数据，链表的结构:")
    print(list(link_list.items()))
    link_list.show()
    # 删除链表数据
    link_list.remove(0)
    print("删除链表数据，链表的结构:")
    print(list(link_list.items()))
    link_list.show()
    # 查找链表数据
    print("查找链表数据，链表的结构")
    print(link_list.find(4))

输出：

参看imooc上liuyubobobo老师java数据结构的python改写：

# -*- coding: utf-8 -*-
# Author:           Annihilation7
# Data:             2018-09-27
# Python version:   3.6

class Node:
    def __init__(self, elem_=None, next_=None):
        """
        节点类构造函数
        :param elem_: 节点所带的元素，默认为None
        :param next_: 指向下一个节点的标签（在python中叫做标签）
        """
        self.elem = elem_
        self.next = next_  # 都是共有的

    def printNode(self):
        """打印Node"""
        print(self.elem, end='  ')  # 就打印一下元素的值


class LinkedList:
    def __init__(self):
        """
        链表构造函数
        """
        self._dummyhead = Node()        # 虚拟头结点，作用巨大，把他当成不属于链表的哨兵节点就好
        # 如果没有dummyhead，在链表头部插入与删除操作将要特殊对待，因为找不到待操作节点的前一个节点
        # 而有了虚拟头结点后，就不存在这种情况了
        self._size = 0       # 容量

    def getSize(self):
        """
        获得链表中节点的个数
        :return: 节点个数
        """
        return self._size

    def isEmpty(self):
        """
        判断链表是否为空
        :return: bool值，空为True
        """
        return self.getSize() == 0

    def add(self, index, elem):
        """
        普适性的插入功能
        时间复杂度：O(n)
        :param index: 要插入的位置（注意index对于用户来说也是从零开始的，这里我没做更改）
        :param elem: 待插入的元素
        """
        if index < 0 or index > self._size:     # 有效性检查
            raise Exception('Add failed. Illegal index')
        prev = self._dummyhead      # 从虚拟头结点开始，注意虚拟头结点不属于链表内的节点，当做哨兵节点来看就好了
        for i in range(index):      # 往后撸，直到待操作节点的前一个节点
            prev = prev.next
        prev.next = Node(elem, prev.next)
        # 先看等式右边，创建了一个节点对象，携带的元素是elem，指向的元素就是index处的节点，即
        # 现在有一个新的节点指向了index处的节点
        # 并将它赋给index节点处的前一个节点的next，是的prev的下一个节点就是这个新节点，完成拼接操作
        # 可以分解成三句话：  temp = Node(elem); temp.next = prev.next; prev.next = temp
        # 画个图就很好理解啦
        self._size += 1 # 维护self._size

    def addFirst(self, elem):
        """
        将elem插入到链表头部
        时间复杂度：O(1)
        :param elem: 要插入的元素
        """
        self.add(0, elem)       # 直接点用self.add

    def addLast(self, elem):
        """
        链表尾部插入元素elem
        时间复杂度：O(n)
        :param elem: 待插入的元素
        """
        self.add(self._size, elem)      # 调用self.add

    def remove(self, index):
        """
        删除第index位置的节点
        时间复杂度：O(n)
        :param index: 相应的位置，注意从零开始
        :return: 被删除节点的elem成员变量
        """
        if index < 0 or index >= self.getSize():    # index合法性检查
            raise Exception('Remove falied. Illegal index')
        pre = self._dummyhead       # 同样的，要找到待删除的前一个节点，所以从dummyhead开始
        for i in range(index):      # 往后撸index个节点
            pre = pre.next
        retNode = pre.next          # 此时到达待删除节点的前一个节点，并用retNode对待删除节点进行标记，方便返回elem
        pre.next = retNode.next     # pre的next直接跨过待删除节点直接指向待删除节点的next，画个图就很好理解了
        retNode.next = None         # 待删除节点的next设为None，让它完全从链表中脱离，使得其被自动回收
        self._size -= 1             # 维护self._size
        return retNode.elem         # 返回被删除节点的elem成员变量

    def removeFirst(self):
        """
        删除第一个节点(index=0)
        时间复杂度：O(1)
        :return: 第一个节点的elem成员变量
        """
        return self.remove(0)   # 直接调用self.add方法

    def removeLast(self):
        """
        删除最后一个节点(index=self._size-1)
        时间复杂度：O(n)
        :return: 最后一个节点的elem成员变量
        """
        return self.remove(self.getSize() - 1)

    def removeElement(self, elem):
        """
        删除链表的指定元素elem，这个方法实现的是将链表中为elem的Node全部删除哦，与数组只删除最左边的第一个是不一样的！如果elem不存在我们什么也不做
        :param elem: 待删除的元素elem
        时间复杂度：O(n)
        """
        pre = self._dummyhead             # 老方法，被删除元素的前一个记为pre
        while pre.next:                   # 只要pre的next不为空
            if pre.next.elem == elem:     # pre的next的elem和elem相等
                delNode = pre.next        # 记下pre的next的节点，准备略过它
                pre.next = delNode.next   # 略过pre.next直接将pre.next置为pre.next.next
                delNode.next = None       # delNode的next置为空，被当成垃圾回收
                self._size -= 1           # 维护self._size
                # 注意此时不要pre = pre.next，因为这时候pre的next又是一个新的元素！也需要进行判断的，所以删除的是所有携带值为elem的节点
            else:
                pre = pre.next            # 不相等就往后撸就完事了


    def get(self, index):
        """
        获得链表第index位置的值
        时间复杂度：O(n)
        :param index: 可以理解成索引，但并不是索引！
        :return: 第index位置的值
        """
        if index < 0 or index >= self.getSize():    # 合法性检查
            raise Exception('Get failed.index is Valid, index require 0<=index<=self._size-1')
        cur = self._dummyhead.next      # 初始化为第一个有效节点
        for i in range(index):          # 执行index次
            cur = cur.next              # 往后撸，一直到第index位置
        return cur.elem

    def getFirst(self):
        """
        获取链表第一个节点的值
        时间复杂度：O(1)
        :return: 第一个节点的elem
        """
        return self.get(0)      # 调用self.add方法

    def getLast(self):
        """
        获取链表最后一个节点的值
        时间复杂度：O(n)
        :return: 最后一个节点的elem
        """
        return self.get(self.getSize() - 1)

    def set(self, index, e):
        """
        把链表中第index位置的节点的elem设置成e
        时间复杂度：O(n)
        :param index: 链表中要操作的节点的位置
        :param e:  将要设为的值
        """
        if index < 0 or index >= self.getSize():        # 合法性检查
            raise Exception('Set failed.index is Valid, index require 0<=index<=self._size-1')
        cur = self._dummyhead.next  # 从第一个元素开始，也就是dummyhead的下一个节点
        for i in range(index):      # 往后撸，直到要操作的节点的位置
            cur = cur.next
        cur.elem = e        # 设置成e即可

    def contains(self, e):
        """
        判断链表的节点的elem中是否存在e
        时间复杂度：O(n)
        由于并不存在索引，所以只能从头开始找，一直找。。。如果到尾还没找到就是不存在
        :param e: 要判断的值
        :return: bool值，存在为True
        """
        cur = self._dummyhead.next  # 将cur设置成第一个节点
        while cur != None:      # 只要cur有效，注意这个链表的最后一个节点一定是None，因为dummyhead初始化时next就是None，这个
            # 通过链表的这些方法只会往后移动，一直处于最末尾
            if cur.elem == e:   # 如果相等就返回True
                return True
            cur = cur.next      # 否则就往后撸
        return False            # 到头了还没找到就返回False

    def printLinkedList(self):
        """对链表进行打印操作"""
        cur = self._dummyhead.next
        print('表头：', end=' ')
        while cur != None:
            cur.printNode()
            cur = cur.next
        print('\nSize:  %d' % self.getSize())

+++++++++++++++++==+++++++++++++++++=+=++++++++++++++++++++
import linkedlist       # Linkedlist写在这个py文件中
import numpy as np
np.random.seed(7)

test = linkedlist.LinkedList()
print(test.getSize())
print(test.isEmpty())
test.addFirst(6)
for i in range(13):
    test.addLast(np.random.randint(11))
test.printLinkedList()
test.add(10, 'annihilation7')
test.printLinkedList()
print(test.getSize())
print(test.get(2))
print(test.getLast())
print(test.getFirst())
test.set(0, 30)
test.printLinkedList()
print(test.contains(13))
print(test.remove(8))
test.printLinkedList()
print(test.removeFirst())
test.printLinkedList()
print(test.removeLast())
test.printLinkedList()

print('删除全部为7的元素：')
test.removeElement(7)
test.printLinkedList()
print(test.getSize())

5.2 双链表

这里就要使用到双链表了，相比单链表来说，每个节点既保存了指向下一个节点的指针，同时还保存了上一个节点的指针。

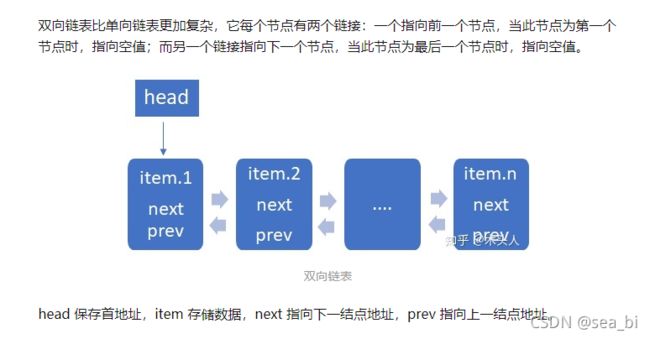
寻找一个双链表的图:

class Node(object):
    """双向链表的结点"""
    def __init__(self, item):
        # item存放数据元素
        self.item = item
        # next 指向下一个节点的标识
        self.next = None
        # prev 指向上一结点
        self.prev = None

class BilateralLinkList(object):
    """双向链表"""

    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def length(self):
        """链表长度"""
        # 初始指针指向head
        cur = self._head
        count = 0
        # 指针指向None 表示到达尾部
        while cur is not None:
            count += 1
            # 指针下移
            cur = cur.next
        return count

    def items(self):
        """遍历链表"""
        # 获取head指针
        cur = self._head
        # 循环遍历
        while cur is not None:
            # 返回生成器
            yield cur.item
            # 指针下移
            cur = cur.next

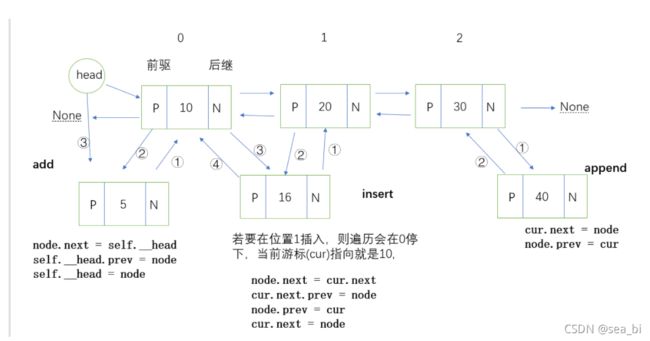
    def add(self, item):
        """向链表头部添加元素"""
        node = Node(item)
        if self.is_empty():
            # 头部结点指针修改为新结点
            self._head = node
        else:
            # 待插入节点的后继区指向原头节点
            node.next = self._head
            # 原头节点的前驱区指向待插入节点
            self._head.prev = node
            # head 指向新结点
            self._head = node

    def append(self, item):
        """尾部添加元素"""
        node = Node(item)
        if self.is_empty():  # 链表无元素
            # 头部结点指针修改为新结点
            self._head = node
        else:  # 链表有元素
            # 移动到尾部
            cur = self._head
            while cur.next is not None:
                cur = cur.next
            # 新结点上一级指针指向旧尾部
            node.prev = cur
            # 旧尾部指向新结点
            cur.next = node

    def insert(self, index, item):
        """ 指定位置插入元素"""
        if index <= 0:
            self.add(item)
        elif index > self.length() - 1:
            self.append(item)
        else:
            # 单向链表中为了在特定位置插入，要先在链表中找到待插入位置和其前一个位置
            # 双向链表中就不需要两个游标了（当然单向链表中一个游标也是可以只找前一个位置）
            node = Node(item)
            cur = self._head
            for i in range(index):
                cur = cur.next
            # 此时的游标指向pos的前一个位置
            # 这里的相互指向需尤为注意，有多种实现，需细细分析
            # 新结点的向下指针指向当前结点
            node.next = cur
            # 新结点的向上指针指向当前结点的上一结点
            node.prev = cur.prev
            # 当前上一结点的向下指针指向node
            cur.prev.next = node
            # 当前结点的向上指针指向新结点
            cur.prev = node

    def remove(self, item):
        """ 删除结点 """
        if self.is_empty():
            return
        cur = self._head
        # 删除元素在第一个结点
        if cur.item == item:
            # 只有一个元素
            if cur.next is None:
                self._head = None
                return True
            else:
                # head 指向下一结点
                self._head = cur.next
                # 下一结点的向上指针指向None
                cur.next.prev = None
                return True
        # 移动指针查找元素
        while cur.next is not None:
            if cur.item == item:
                # 上一结点向下指针指向下一结点
                cur.prev.next = cur.next
                # 下一结点向上指针指向上一结点
                cur.next.prev = cur.prev
                return True
            cur = cur.next
        # 删除元素在最后一个
        if cur.item == item:
            # 上一结点向下指针指向None
            cur.prev.next = None
            return True

    def find(self, item):
        """查找元素是否存在"""
        return item in self.items()

    def show(self):
        if self.is_empty():
            print("空链表")
            return None
        cur = self._head
        while cur is not None:
            print(cur.item, end="-->")
            cur = cur.next
        print("\n")


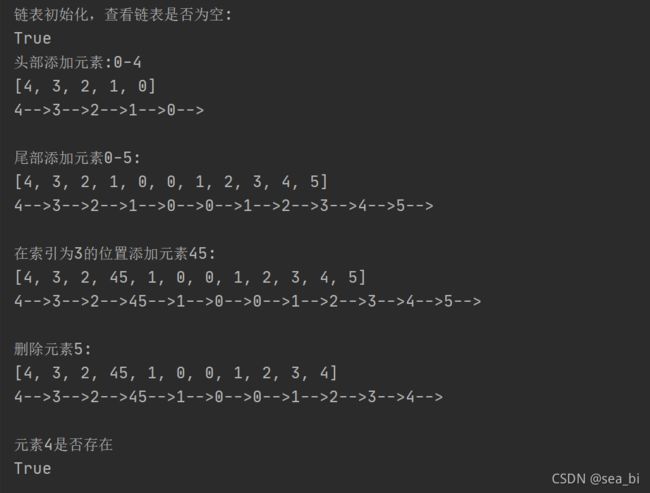
if __name__ == '__main__':
    link_list = BilateralLinkList()
    print("链表初始化，查看链表是否为空:")
    print(link_list.is_empty())

    # 头部添加元素
    for i in range(5):
        link_list.add(i)
    print("头部添加元素:0-4")
    print(list(link_list.items()))
    link_list.show()
    # 尾部添加元素
    for i in range(6):
        link_list.append(i)
    print("尾部添加元素0-5:")
    print(list(link_list.items()))
    link_list.show()
    # 添加元素
    link_list.insert(3, 45)
    print("在索引为3的位置添加元素45:")
    print(list(link_list.items()))
    link_list.show()
    # 删除元素
    link_list.remove(5)
    print("删除元素5:")
    print(list(link_list.items()))
    link_list.show()
    # 元素是否存在
    print("元素4是否存在")
    print(4 in link_list.items())

结果：

这里最难得是：

  def add(self, item):
        """向链表头部添加元素"""
        node = Node(item)
        if self.is_empty():
            # 头部结点指针修改为新结点
            self._head = node
        else:
            # 新结点指针指向原头部结点
            node.next = self._head
            # 原头部 prev 指向 新结点
            self._head.prev = node
            # head 指向新结点
            self._head = node

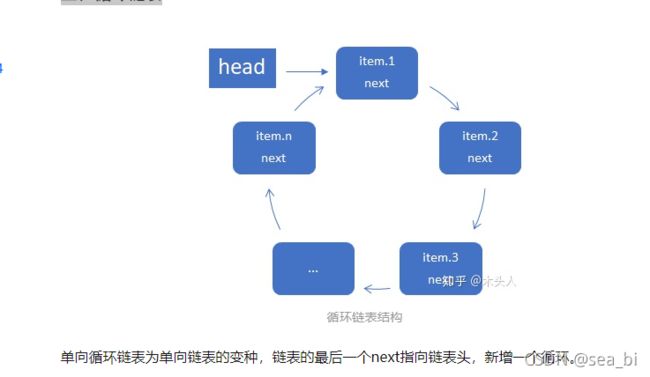
5.3 循环链表

class Node(object):
    """链表的结点"""

    def __init__(self, item):
        # item存放数据元素
        self.item = item
        # next是下一个节点的标识
        self.next = None


class SingleCycleLinkList(object):

    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def length(self):
        """链表长度"""
        # 链表为空
        if self.is_empty():
            return 0
        # 链表不为空
        count = 1
        cur = self._head
        while cur.next != self._head:
            count += 1
            # 指针下移
            cur = cur.next
        return count

    def items(self):
        """ 遍历链表 """
        # 链表为空
        if self.is_empty():
            return
        # 链表不为空
        cur = self._head
        while cur.next != self._head:
            yield cur.item
            cur = cur.next
        yield cur.item

    def add(self, item):
        """ 头部添加结点"""
        node = Node(item)
        if self.is_empty():  # 为空
            self._head = node
            node.next = self._head
        else:
            # 添加结点指向head
            node.next = self._head
            cur = self._head
            # 移动结点，将末尾的结点指向node
            while cur.next != self._head:
                cur = cur.next
            cur.next = node
        # 修改 head 指向新结点
        self._head = node

    def append(self, item):
        """尾部添加结点"""
        node = Node(item)
        if self.is_empty():  # 为空
            self._head = node
            node.next = self._head
        else:
            # 寻找尾部
            cur = self._head
            while cur.next != self._head:
                cur = cur.next
            # 尾部指针指向新结点
            cur.next = node
            # 新结点指针指向head
            node.next = self._head

    def insert(self, index, item):
        """ 指定位置添加结点"""
        if index <= 0:  # 指定位置小于等于0，头部添加
            self.add(item)
        # 指定位置大于链表长度，尾部添加
        elif index > self.length() - 1:
            self.append(item)
        else:
            node = Node(item)
            cur = self._head
            # 移动到添加结点位置
            for i in range(index - 1):
                cur = cur.next
            # 新结点指针指向旧结点
            node.next = cur.next
            # 旧结点指针 指向 新结点
            cur.next = node

    def remove(self, item):
        """ 删除一个结点 """
        if self.is_empty():
            return
        cur = self._head
        pre = Node
        # 第一个元素为需要删除的元素
        if cur.item == item:
            # 链表不止一个元素
            if cur.next != self._head:
                while cur.next != self._head:
                    cur = cur.next
                # 尾结点指向 头部结点的下一结点
                cur.next = self._head.next
                # 调整头部结点
                self._head = self._head.next
            else:
                # 只有一个元素
                self._head = None
        else:
            # 不是第一个元素
            pre = self._head
            while cur.next != self._head:
                if cur.item == item:
                    # 删除
                    pre.next = cur.next
                    return True
                else:

                    pre = cur  # 记录前一个指针
                    cur = cur.next  # 调整指针位置
        # 当删除元素在末尾
        if cur.item == item:
            pre.next = self._head
            return True

    def find(self, item):
        """ 查找元素是否存在"""
        return item in self.items()

    def show(self):
        if self.is_empty():
            print("空链表")
            return None
        cur=self._head
        while cur.next != self._head:
            print(cur.item,end="-->")
            cur=cur.next
        print(cur.item)



if __name__ == '__main__':
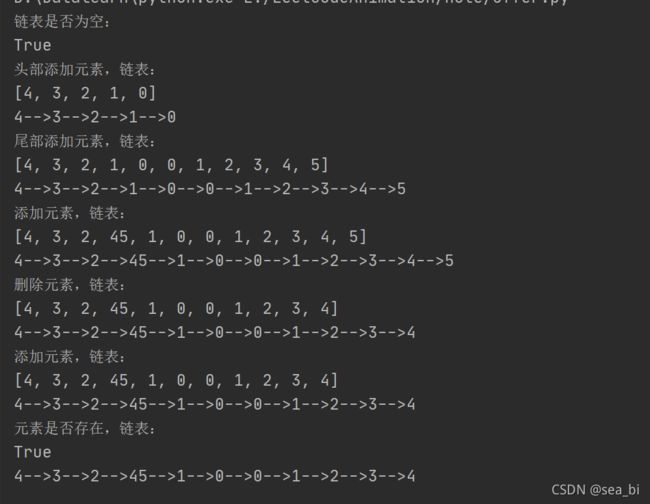
    link_list = SingleCycleLinkList()
    print("链表是否为空：")
    print(link_list.is_empty())
    # 头部添加元素
    for i in range(5):
        link_list.add(i)
    print("头部添加元素，链表：")
    print(list(link_list.items()))
    link_list.show()
    # 尾部添加元素
    for i in range(6):
        link_list.append(i)
    print("尾部添加元素，链表：")
    print(list(link_list.items()))
    link_list.show()
    # 添加元素
    link_list.insert(3, 45)
    print("添加元素，链表：")
    print(list(link_list.items()))
    link_list.show()
    # 删除元素
    print("删除元素，链表：")
    link_list.remove(5)
    print(list(link_list.items()))
    link_list.show()
    print("添加元素，链表：")
    print(list(link_list.items()))
    link_list.show()
    # 元素是否存在
    print("元素是否存在，链表：")
    print(4 in link_list.items())
    link_list.show()

输出结果：

5.4 剑指Offer例题

5.4.1【剑指Offer】3、从尾到头打印链表

题目描述：
输入一个链表，按链表值从尾到头的顺序返回一个ArrayList。

思路：从头到尾遍历一遍链表，把它所有的值存到一个栈里，利用栈的先入后出特性，完成从尾到头打印。由于这个题里的输出需要时一个列表，所以这里利用列表作为存储结果，每次都存储到列表的第一个位置（伪装是栈），然后将列表返回。

看完这个图，实现代码：

class ListNode:
    def __init__(self,x):
        self.val=x
        self.next=None

class Soultion:
    # 返回从尾部到头部的列表值序列，例如[1,2,3]
    def printListFromTailToHead(self, listNode):
        l=[]
        h=listNode # 用h代替listNode遍历
        while h is not None: # 停止条件，遍历到了链表的最后一个节点
            l.insert(0,h.val) # 向栈压入数值，模拟栈的push操作
            h=h.next # 接着遍历
        return l



if __name__ == "__main__":
    l=ListNode(1)
    l2=ListNode(2)
    l2.next=ListNode(3)
    l.next=l2

    s = Soultion()
    res = s.printListFromTailToHead(l)
    print(res)

输出结果：
[3, 2, 1]

5.4.2【剑指Offer】14、链表中倒数第k个结点

题目描述：

输入一个链表，输出该链表中倒数第k个结点。
为了符合习惯，从1开始计数，即链表的尾结点是倒数第1个节点。例如，一个链表有6个结点，从头结点开始，它们的值依次是1,2,3,4,5,6。则这个链表倒数第三个结点是值为4的结点。

解题思路：
对于单链表来说，没有从后向前的指针，因此一个直观的解法是先进行一次遍历，统计出链表中结点的个数n，第二次再进行一次遍历，找到第n-k+1个结点就是我们要找的结点，但是这需要对链表进行两次遍历。
为了实现一次遍历，我们这里采用双指针解法。我们可以定义两个指针，第一个指针从链表的头指针开始先向前走k步，第二个指针保持不动，从第k+1步开始，第二个指针也从头开始前进，两个指针都每次前进一步。这样，两个指针的距离都一直保持在k，当快指针（走在前面的）到达null时，慢指针（走在后面的）正好到达第k个结点。注意：要时刻留意空指针的判断。

class ListNode:
    def __init__(self,x):
        self.val=x
        self.next=None

class Solution:
    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def add(self, item):
        """尾部添加元素"""
        node = ListNode(item)
        # 先判断是否为空链表
        if self.is_empty():
            # 空链表，_head 指向新结点
            self._head = node
        else:
            # 不是空链表，则找到尾部，将尾部next结点指向新结点
            cur = self._head
            while cur.next is not None:
                cur = cur.next
            cur.next = node


    def FindKthToTail(self, k):
    #将双指针都
        a,b=self._head,self._head
        #先让一个节点先走k步
        for i in range(k):
            #判断是否存在
            if b:
                b=b.next
            else:
                return None
        while b:
            a,b=a.next,b.next
        return a


if __name__=="__main__":
    # 头部添加元素
    link_list=Solution()
    for i in range(6):
        link_list.add(i)

    res=link_list.FindKthToTail(4)
    print(res.val)

输出结果：2

数据调试，节点加入了

5.4.3 【剑指Offer】15、反转链表

题目描述：
输入一个链表，反转链表后，输出新链表的表头。

解法1：
唯有经典套路得人心，这里思路比较简单！用pre表示前一个节点，cur表示当前节点，pre和cur交替向前移动，每次移动都将cur的next指向pre，直到链表的尽头。

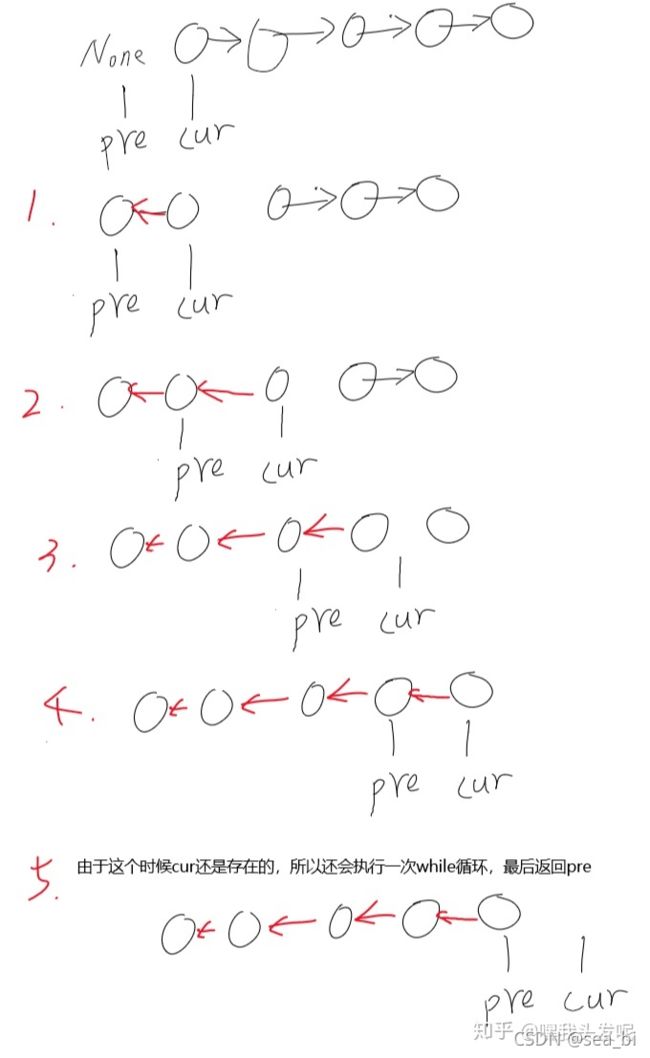
实现代码：

class ListNode:
    def __init__(self,x):
        self.val=x
        self.next=None

class Solution:
    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def add(self, item):
        """尾部添加元素"""
        node = ListNode(item)
        # 先判断是否为空链表
        if self.is_empty():
            # 空链表，_head 指向新结点
            self._head = node
        else:
            # 不是空链表，则找到尾部，将尾部next结点指向新结点
            cur = self._head
            while cur.next is not None:
                cur = cur.next
            cur.next = node
        return self._head

    def ReverseList(self, head):
        cur,pre=head,None
        if head==None or head.next==None:
            return head
        while cur:
            tmp=cur.next
            cur.next=pre
            pre=cur
            cur=tmp
        return pre

    def items(self,head):
        if head==None:
            return
        cur=head
        while cur:
            print(cur.val,end="-->")
            cur=cur.next



if __name__=="__main__":
    # 头部添加元素
    link_list=Solution()
    for i in range(6):
        cur=link_list.add(i)

    res=link_list.ReverseList(cur)
    link_list.items(res)

输出结果：
5–>4–>3–>2–>1–>0–>

解法2：三指针。使用三个指针，分别指向当前遍历到的结点、它的前一个结点以及后一个结点。将指针反转后，三个结点依次前移即可。

class ListNode:
    def __init__(self,x):
        self.val=x
        self.next=None

class Solution:
    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def add(self, item):
        """尾部添加元素"""
        node = ListNode(item)
        # 先判断是否为空链表
        if self.is_empty():
            # 空链表，_head 指向新结点
            self._head = node
        else:
            # 不是空链表，则找到尾部，将尾部next结点指向新结点
            cur = self._head
            while cur.next is not None:
                cur = cur.next
            cur.next = node
        return self._head

    def ReverseList(self, head):

        if head==None or head.next==None:
            return head
        first, second, third = None, head, head.next
        while third:
            second.next = first # 三指针之间的变换
            first = second
            second = third
            third = third.next
        second.next=first
        return second

    def items(self,head):
        if head==None:
            return
        cur=head
        while cur:
            print(cur.val,end="-->")
            cur=cur.next



if __name__=="__main__":
    # 头部添加元素
    link_list=Solution()
    for i in range(6):
        cur=link_list.add(i)

    res=link_list.ReverseList(cur)
    link_list.items(res)

输出结果：
5–>4–>3–>2–>1–>0–>

两种方法都是差不多。

5.4.4 【剑指Offer】16、合并两个排序的链表

题目描述：
输入两个单调递增的链表，输出两个链表合成后的链表，当然我们需要合成后的链表满足单调不减规则。

思路：可以考虑递归法和非递归法两种解法。假设有两个链表，头节点分别为head1和head2.

递归法，用res存储最终结果的头节点：
如果某一个链表为空，返回另一个即可；
如果p1的值小于p2的值，说明p1应该是结果链表的头节点，res.next就在p1.next和p2里面继续找；
如果p1的值大于p2的值，说明p2应该是结果链表的头节点，res.next就在p2.next和p1里面继续找。

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None


class Solution:
    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def add(self, item):
        """尾部添加元素"""
        node = ListNode(item)
        # 先判断是否为空链表
        if self.is_empty():
            # 空链表，_head 指向新结点
            self._head = node
        else:
            # 不是空链表，则找到尾部，将尾部next结点指向新结点
            cur = self._head
            while cur.next is not None:
                cur = cur.next
            cur.next = node
        return self._head

    def Merge(self, head1, head2):

        if head1 == None:
            return head2
        if head2 == None:
            return head1
        if head1.val <= head2.val:
            res = head1
            res.next = self.Merge(head1.next, head2)
        else:
            res = head2
            res.next = self.Merge(head1,head2.next) 
        return res

    def items(self, head):
        if head == None:
            return
        cur = head
        while cur:
            print(cur.val, end="-->")
            cur = cur.next


if __name__ == "__main__":
    # 头部添加元素
    link_list = Solution()
    for i in [1,3,5,7]:
        head1 = link_list.add(i)
    link_list2 = Solution()
    for i in [2,4,6,8]:
        head2 = link_list2.add(i)

    res = link_list.Merge(head1, head2)
    link_list.items(res)

输出：
1–>2–>3–>4–>5–>6–>7–>8–>

解法2：
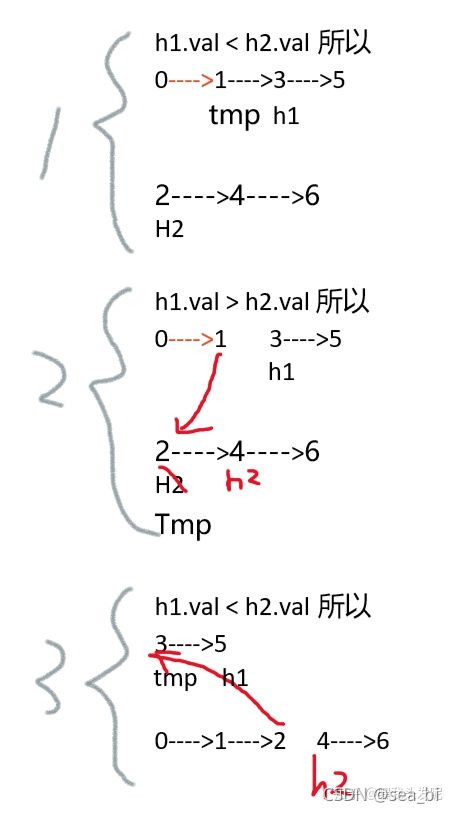
非递归法：
用head1，head2指向剩余没有被分好顺序的链表；
用tmp表示当前要被分配的链表节点；
如果head1.val <= head2.val，就让tmp指向head1， head1指向它的下一个节点。意思是现在准备分配head1，因为它比较小。
如果head1.val > head2.val，就让tmp指向head2， head2指向它的下一个节点。意思是现在准备分配head2，因为它比较小。

class ListNode:
    def __init__(self, x):
        self.val = x
        self.next = None


class Solution:
    def __init__(self):
        self._head = None

    def is_empty(self):
        """判断链表是否为空"""
        return self._head is None

    def add(self, item):
        """尾部添加元素"""
        node = ListNode(item)
        # 先判断是否为空链表
        if self.is_empty():
            # 空链表，_head 指向新结点
            self._head = node
        else:
            # 不是空链表，则找到尾部，将尾部next结点指向新结点
            cur = self._head
            while cur.next is not None:
                cur = cur.next
            cur.next = node
        return self._head

    def Merge(self, head1, head2):
        if head1 == None:
            return head2
        if head2 == None:
            return head1
        tmp = ListNode(0)
        head = tmp
        if head1.val <= head2.val:
            head.next = head1
        else:
            head.next = head2
        while head1 and head2:
            if head1.val <= head2.val:
                tmp.next = head1
                head1 = head1.next
            else:
                tmp.next = head2
                head2 = head2.next
            tmp = tmp.next
        if head1:
            tmp.next = head1
        else:
            tmp.next = head2
        return head.next #去掉头结点

    def items(self, head):
        if head == None:
            return
        cur = head
        while cur:
            print(cur.val, end="-->")
            cur = cur.next


if __name__ == "__main__":
    # 头部添加元素
    link_list = Solution()
    for i in [1,3,5,7]:
        head1 = link_list.add(i)
    link_list2 = Solution()
    for i in [2,4,6,8]:
        head2 = link_list2.add(i)

    res = link_list.Merge(head1, head2)
    link_list.items(res)

输出结果：
1–>2–>3–>4–>5–>6–>7–>8–>

6 队列和栈

前面讲了线性和链式结构，如果你顺利掌握了，下边的队列和栈就小菜一碟了。因为我们会用前两章讲到的东西来实现队列和栈。之所以放到一起讲是因为这两个东西很类似，队列是先进先出结构(FIFO, first in first out)，栈是后进先出结构(LIFO, last in first out)。
首先讲下队列。

6.1 队列Queue

只允许在一端插入数据操作，在另一端进行删除数据操作的特殊线性表；进行插入操作的一端称为队尾（入队列），进行删除操作的一端称为队头（出队列）；队列具有先进先出（FIFO）的特性。

6.1.1 用数组实现顺序队列


class List_Queue(object):
    # 初始化数组
    def __init__(self,elems=[]):
        self.items=elems

    def is_Empy(self):
        return self.items==[]

    def pop(self):
        self.items.pop(0)

    def insert(self,item):
        self.items.append(item)

    def size(self):
        return len(self.items);

    def print(self):
        print("\n")
        for i in self.items:
            print(i,end=",")


if __name__=="__main__":
    my_list=List_Queue([1,2,3,4,5])
    my_list.print()
     # 入队
    my_list.insert(88)
    my_list.insert(99)
    my_list.print()
    #出队
    my_list.pop()
    my_list.print()

输出结果：

6.1.2 双端队列

双端队列又名double ended queue，简称deque，双端队列没有队列和栈这样的限制级，它允许两端进行入队和出队操作，也就是说元素可以从队头出队和入队，也可以从队尾出队和入队。

class SequenceDoubleQueue(object):

    def __init__(self,elems=[]):
        self.items=elems

    def is_empty(self):
        return self.items==[]

    def show(self):
        print("\n")
        if self.is_empty():
            print("队列为空。")
            return
        for i in self.items:
            print(i,end=",")

    # 头部插入
    def head_insert(self,data):
        self.items.insert(0,data)
    #头部出队
    def head_outer(self):
        if self.is_empty():
            return
        return self.items.pop(0)

    # 尾部插入
    def end_insert(self, data):
        self.items.append(data)

    # 尾部出队
    def end_outer(self):
        if self.is_empty():
            return
        return self.items.pop()

    def size(self):
        return len(self.items)

if __name__=="__main__":
    sdq=SequenceDoubleQueue([1,2,3,4,5])
    sdq.head_insert('x')
    sdq.head_insert('y')
    sdq.head_insert('z')
    sdq.end_insert(10)
    sdq.show()
    sdq.head_outer()
    sdq.end_outer()
    sdq.show()

输出结果：

z,y,x,1,2,3,4,5,10,

y,x,1,2,3,4,5,

今天学习就到这了。

6.13 循环队列

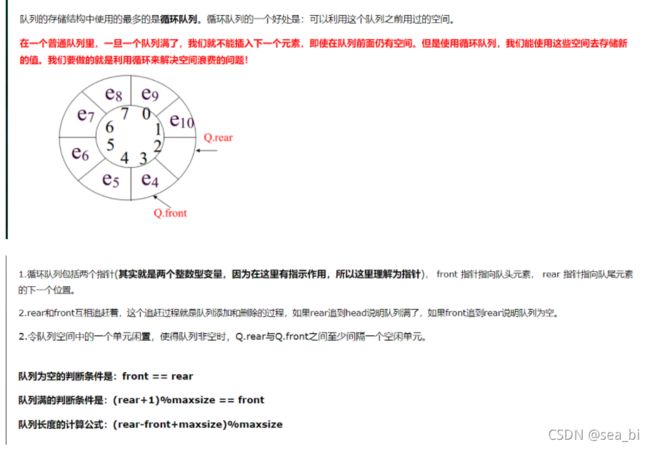
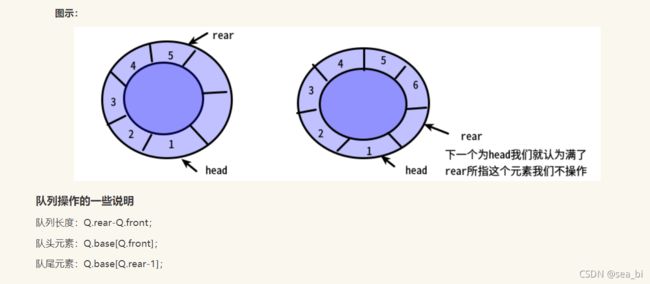
maxsize表示循环队列的最大容纳量，其表示队列的全部可操作空间。

rear代表尾指针，入队时移动。

front代表头指针，出队时移动。

class SqQueue(object):
    def __init__(self, maxsize):
        self.queue = [None] * maxsize
        self.maxsize = maxsize
        self.front = 0
        self.rear = 0

    # 返回当前队列的长度
    def QueueLength(self):
        return (self.rear - self.front + self.maxsize) % self.maxsize

    # 如果队列未满，则在队尾插入元素，时间复杂度O(1)
    def EnQueue(self, data):
        if (self.rear + 1) % self.maxsize == self.front:
            print("The queue is full!")
        else:
            self.queue[self.rear] = data
           # self.queue.insert(self.rear,data)
            self.rear = (self.rear + 1) % self.maxsize

    # 如果队列不为空，则删除队头的元素,时间复杂度O(1)
    def DeQueue(self):
        if self.rear == self.front:
            print("The queue is empty!")
        else:
            data = self.queue[self.front]
            self.queue[self.front] = None
            self.front = (self.front + 1) % self.maxsize
            return data


    # 输出队列中的元素
    def ShowQueue(self):
        for i in range(self.maxsize):
            print(self.queue[i],end=',')
        print(' ')


if __name__ == '__main__':
    my_Queue=SqQueue(4)
    #入栈
    my_Queue.EnQueue(1)
    my_Queue.EnQueue(7)
    my_Queue.EnQueue(8)
    my_Queue.EnQueue(6)
    my_Queue.ShowQueue()

输出结果：
The queue is full!
1,7,8,None,

由于令队列中会有一个空闲的单位，使得队列不为空，Q.rear和Q.front之间隔一个空闲的单元。

6.2 栈

栈的定义，即栈是一种只能从表的一端存取数据且遵循 “先进后出” 原则的线性存储结构。

基于栈结构的特点，在实际应用中，通常只会对栈执行以下两种操作：
1、向栈中添加元素，此过程被称为"进栈"（入栈或压栈）；
2、从栈中提取出指定元素，此过程被称为"出栈"（或弹栈）；

对于栈的常用操作：
1、stack(): 建立一个空的栈对象。

2、push(): 把一个元素添加到栈顶。

3、pop():删除栈的顶层元素，并返回这个元素。

4、peek():返回顶层的元素，并不删除它。

5、isEmpty():判断栈是否为空。

6、size():返回栈中元素的个数。

由于栈数据结构只允许在一端进行操作，因而按照后进先出的原理运作。
栈可以用顺序表实现，也可以用链表实现。

class Stack(object):
    def __init__(self):
        self.items=[]

    # 判断栈是否为空，返回布尔值
    def is_Empty(self):
        return self.items==[]

    # 返回栈顶元素
    def peek(self):
        return self.items[-1]

    def size(self):
        return len(self.items)

    # 入栈
    def push(self,item):
        return self.items.append(item)

    # 把栈顶元素弹出去
    def pop(self):
        return self.items.pop()

    # 返回栈的数据
    def print(self):
        return self.items

if __name__=="__main__":
    my_stack = Stack()
    # 入栈
    my_stack.push(1)
    my_stack.push(7)
    my_stack.push(8)
    my_stack.push(6)
    my_print = my_stack.print()
    print(my_print)

结果：
[1, 7, 8, 6]

6.3 剑指Offer例题

6.3.1【剑指Offer】5、用两个栈实现队列

题目描述：
用两个栈来实现一个队列，完成队列的Push和Pop操作。队列中的元素为int类型。

思路：队列是先入先出，栈是先入后出。考虑用一个栈s2存储数据，另一个栈s1用于当存在队列pop操作时用于接纳s1中的数据。话不多说，整个栗子：

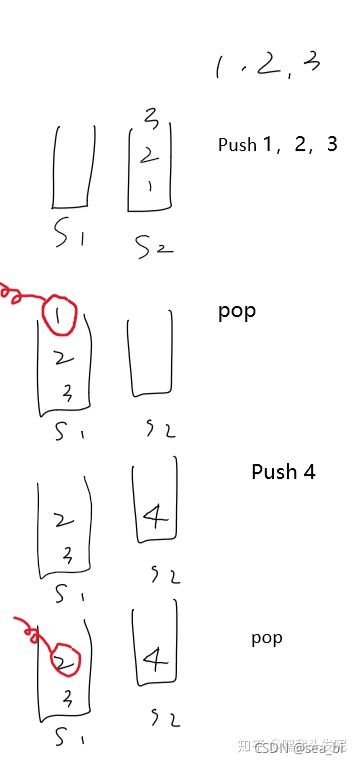
class Solution:
    def __init__(self):
        self.s1=[] # list push操作接受数据
        self.s2=[] # pop输出数据

    def push(self,x):
        if len(self.s2)==0:
            self.s1.append(x)
    def pop(self):
        while len(self.s1)!=0:
            # pop() 函数用于移除列表中的一个元素（默认最后一个元素），并且返回该元素的值。
            self.s2.append(self.s1.pop())
        return self.s2.pop()




if __name__ == "__main__":
    s=Solution()
    #插入数据
    s.push(1)
    s.push(2)
    s.push(3)
    #输出数据
    for i in range(3):
        print(s.pop(),end=",")

输出结果：
1,2,3,

看到有的博客进行扩展，
解题思路：
本题的基本意图是：用两个后入先出的栈来实现先入先出的队列。对于这个问题，我们可以通过一个实例来进行具体分析。不难得出相应的规律：有两个栈stack1和stack2，每次向队列中插入元素可以都压入到stack1中，当需要从队列中删除元素时，我们应该是删除最早插入的那个（FIFO），这时可以将stack1中的元素逐个弹出并压入stack2，直到stack1为空，这时最早插入的元素就位于stack2的栈顶，可以直接弹出。
因此，我们总结如下：压入元素时，都压入栈1，当需要弹出时，从栈2弹出，当栈2不为空时直接弹出栈顶元素，为空时将栈1的元素“倒进去”。

Java实现：

public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
   
    public void push(int node) {
        stack1.push(node);
    }
    
    public int pop() {
        if(stack2.empty()){  //为空时将栈1的元素“倒进去”
            while(!stack1.empty()){
                stack2.push(stack1.pop());
            }
        }
        return stack2.pop();
    }
}

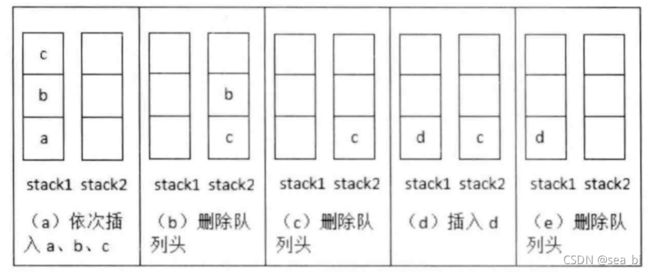
扩展：用两个队列实现一个栈
用两个队列实现栈相比稍微复杂，当插入一个元素时，可以选择不为空的那个队列直接加进去，而当删除一个元素时，需要借助另一个空队列，首先依次删除原队列的头，并将删除的元素加入另一个队列，直到找到队列最后一个元素，将其删除，这时原来的数据队列变空，另一个队列变为数据栈。

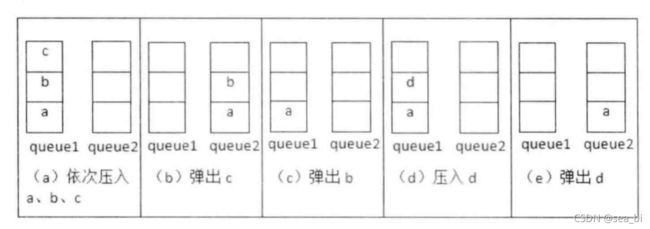
首先要知道栈和队列的特点，栈是后进先出，（单向）队列是后进后出（先进先出）；就以列表作为队列的底层实现，只要保证先进先出的约束就是队列。这里只实现进栈和出栈两个操作。

class Solution:
    # 实现一个队列的功能
    def __init__(self):
        self.accept_stack = []  # 先用来接收数据的栈
        self.output_stack = []  # 后用来输出的栈

    def push(self, node):  # 往第一个栈里添加元素（栈和队里再存数据是不存在区别的）
        self.accept_stack.append(node)

    def pop(self):  # 通过第二个栈，模拟从队列里取出元素
        if self.accept_stack == []: # 如果输出栈是空，那么我们需要从第一个栈添加元素
            return None
        while len(self.accept_stack)!=1:
            self.output_stack.append(self.accept_stack.pop(0))
        self.accept_stack, self.output_stack = self.output_stack, self.accept_stack  # 交换队列 A,B的位置，为了下一次的pop
        return self.output_stack.pop()




if __name__ == "__main__":
    s=Solution()
    #插入数据
    s.push(1)
    s.push(2)
    s.push(3)
    #输出数据
    for i in range(3):
        print(s.pop(),end=",")

输出：
3,2,1,

6.3.2【剑指Offer】20、包含min函数的栈

题目描述：
定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的min函数（时间复杂度应为O（1））。

注意：保证测试中不会当栈为空的时候，对栈调用pop()或者min()或者top()方法。
思路：这题主要考察是否能够当栈进行push，pop操作时，更新栈中的最小元素~
用s存储栈内元素，用m存储栈内每次压入后的最小值元素。
self.m最后一个元素就是当前栈内的最小值。
push操作，如果m还没有元素，则将node加入m中；
push操作，如果当前node小于等于当前m中最后一个元素，则将node加入m中；
pop操作，如果当前元素和m中最后一个元素相等，则删除m最后一个元素。
这里解释一下为什么push的时候等于m最后一个元素也要加入m中：

class Solution:
    def __init__(self):
        self.s = [] #辅助列表
        self.m = [] #最小列表

    def push(self, node):
        self.s.append(node)
        if len(self.m) == 0 or node <= self.m[-1]:
            self.m.append(node)

    def pop(self):
        if self.m[-1] == self.s[-1]:
            self.m.pop()
        return self.s.pop()

    def top(self):
        return self.s[-1]

    def min(self):
        return self.m[-1]

    def printmin(self):
        for i in self.m:
            print(i,end=",")

    def printstack(self):
        for i in self.s:
            print(i,end=",")

if __name__ == "__main__":
    s=Solution()
    for i in range(5,1,-1):
        s.push(i)
        s.push(2)
    s.printmin()
    s.pop()
    print("\n")
    s.printmin()

输出：
5,2,2,2,2,2,

5,2,2,2,2,

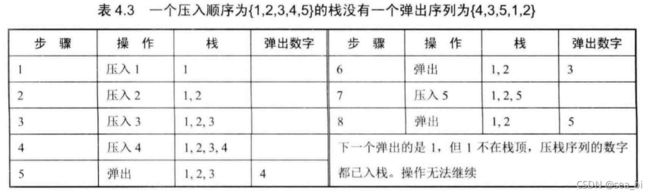
5.4.5 【剑指Offer】21、栈的压入、弹出序列

题目描述：
输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。（注意：这两个序列的长度是相等的）

思路：
用sim列表，模拟栈的push过程和pop过程。相当于sim是一个栈。

当pushV有元素且pushV和popV的最后一个元素一样时，该情况属于刚刚push就pop了，所以将该元素从pushV和popV弹出。比如：pushV:[1,2,3], popV [1,3,2]，这个时候第一个元素1就是刚入栈就出栈，所以把1从pushV和popV中都删除，判断余下元素；
当sim栈的最后一个元素和popV的第一个元素一样的时候，说明现在这个元素按照pop的顺序可以出栈，这个时候把sim和popV的当前元素都删除，判断余下元素；
下一个情况就是，sim栈的最后一个元素和popV的第一个元素不一样的时候，且pushV还有元素的时候，sim继续入栈；
其余情况返回False（这里卡了一下，自己没有想到这么优美的分支）# simulated，存储模拟压栈的过程。

class Solution:
    def IsPopOrder(self, pushV, popV):
        if not pushV or not popV:
            return []
        sim = [] #simulated，存储模拟压栈的过程
        while popV:
            if pushV and popV[0] == pushV[0]:
                popV.pop(0)
                pushV.pop(0)
            elif sim and sim[-1] == popV[0]:
                sim.pop()
                popV.pop(0)
            elif pushV:
                sim.append(pushV.pop(0))
            else: # 其余情况
                return False
        return True

if __name__ == "__main__":
    s=Solution()
    t=s.IsPopOrder([1,2,3,4,5],[4,5,3,2,1])
    print(t)

输出：
True

7 字典

1、字典（也叫映射）
2、结构特点：存储（键，值）数据对的数据结构（Key，Value）。根据键（Key），来寻找值（Value）
3、应用：花名册（学号 -> 人）、车辆管理（车牌号 -> 车）、数据库（id -> 信息）、词频统计（单词 -> 频率）
4、字典容易使用二分搜索树或者链表来实现，比如用二分搜索树来实现，相应的更改一下Node包含的元素就好了

7.1 基于链表的字典

实现：

class Node:
    def __init__(self, key=None, value=None, next=None):
        """
        Description: 节点的构造函数
        Params:
        - key: 传入的键值，默认为None
        - value: 传入的键所对应的value值，默认为None
        - next: 指向下一个Node的标签，默认为None
        """
        self.key = key
        self.value = value
        self.next = next  # 下一个节点为None


class LinkedListDict:
    """以链表作为底层数据结构的字典类"""

    def __init__(self):
        """
        Description: 字典的构造函数
        """
        self._dummyhead = Node()  # 建立一个虚拟头结点，前面讲过，不再赘述
        self._size = 0  # 字典中有效元素的个数

    def getSize(self):
        """
        Description: 获取字典中有效元素的个数
        Returns:
        有效元素的个数
        """
        return self._size

    def isEmpty(self):
        """
        Description: 判断字典是否为空
        Returns:
        bool值，空为True
        """
        return self._size == 0

    def contains(self, key):
        """
        Description: 查看字典的键中是否包含key
        时间复杂度：O(n)
        Params:
        - key: 待查询的键值
        Returns:
        bool值，存在为True
        """
        return self._getNode(key) is not None  # 调用self._getNode私有函数，看返回值是否是None

    def get(self, key):
        """
        Description: 得到字典中键为key的value值
        时间复杂度：O(n)
        Params:
        - key: 待查询的键值
        Returns:
        相应的value值。若key不存在，就返回None
        """
        node = self._getNode(key)  # 拿到键为key的Node
        if node:  # 如果该Node不是None
            return node.value  # 返回对应的value
        else:
            return None  # 否则（此时不存在携带key的Node）返回None

    def add(self, key, value):
        """
        Description: 向字典中添加key，value键值对。若字典中已经存在相同的key，更新其value，否咋在头部添加Node，因为时间复杂度为O(1)
        时间复杂度：O(n)
        Params:
        - key: 待添加的键值
        - value: 待添加的键值的value
        """
        node = self._getNode(key)  # 先判断字典中是否存在这个键
        if node != None:  # 已经存在
            node.value = value  # 更新这个Node的value
        else:
            self._dummyhead.next = Node(key, value, self._dummyhead.next)  # 否则在头部添加，添加操作链表那一章有讲，这里不再赘述
            self._size += 1  # 维护self._size

    def set(self, key, new_value):
        """
        Description: 将字典中键为key的Node的value设为new_value。注意，为防止与add函数发生混淆，
        此函数默认用户已经确信key在字典中，否则报错。并不会有什么新建Node的操作，因为这么做为与add函数有相同的功能，就没有意义了。
        时间复杂度：O(n)
        Params:
        - key: 将要被设定的Node的键
        - new_value: 新的value值
        """
        node = self._getNode(key)  # 找到携带这个key的Node
        if node is None:  # 没找到
            raise Exception('%s doesn\'t exist!' % key)  # 报错就完事了
        node.value = new_value  # 找到了就直接将返回节点的value设为new_value

    def remove(self, key):
        """
        Description: 将字典中键为key的Node删除。注：若不存在携带key的Node，返回Node就好。
        时间复杂度：O(n)
        Params:
        - key: 待删除的键
        Returns:
        被删除节点的value
        """
        pre = self._dummyhead  # 找到要被删除节点的前一个节点（惯用手法，不再赘述）
        while pre.next is not None:  # pre的next只要不为空
            if pre.next.key == key:  # 如果找到了
                break  # 直接break，此时pre停留在要被删除节点的前一个节点
            pre = pre.next  # 否则往后撸

        if pre.next is not None:  # 此时找到了
            delNode = pre.next  # 记录一下要被删除的节点，方便返回其value
            pre.next = delNode.next  # 不再赘述，如果不懂就去看看链表那节吧。O(∩_∩)O
            delNode.next = None  # delNode的下一个节点设为None，使delNode完全与字典脱离，便于垃圾回收器回收
            self._size -= 1  # 维护self._size
            return delNode.value  # 返回被删除节点的value

        return None  # 此时pre的next是None!说明并没有找到这个key，返回None就好了。

    def printLinkedListDict(self):
        """打印字典元素"""
        cur = self._dummyhead.next
        while cur != None:
            print('[Key: %s, Value: %s]' % (cur.key, cur.value), end='-->')
            cur = cur.next
        print('None')

    # private functions
    def _getNode(self, key):
        """
        Description: 一个辅助函数，是私有函数。功能就是返回要查找的键的Node，若key不存在就返回None
        时间复杂度：O(n)
        Params:
        - key: 要查找的键值
        Returns:
        返回带查找key的节点，若不存在返回None
        """
        cur = self._dummyhead.next  # 记录当前节点
        while cur != None:  # cur没到头
            if cur.key == key:  # 找到了
                return cur  # 返回当前的Node
            cur = cur.next  # 没找到就往后撸
        return None  # cur此时为None了。。说明已经到头还没找到，返回None

if __name__=="__main__":
    test_map = LinkedListDict()
    print('初始字典Size：', test_map.getSize())
    print('初始字典是否为空：', test_map.isEmpty())
    for i in range(10):
        test_map.add(i, str(i) + '_index')
    print('10次添加操作后：')
    print('Size: ', test_map.getSize())
    print('是否包含7？', test_map.contains(7))
    test_map.printLinkedListDict()  # 由于在头部插入，所以打印是反向的哦～
    print('键为6的value：', test_map.get(6))
    print('将键值为4的value设为 "你好呀",并打印：')
    test_map.set(4, '你好呀')
    test_map.printLinkedListDict()
    # test_map.set(12, 'debug')
    print('删除键为7的元素，并打印：')
    test_map.remove(7)
    test_map.printLinkedListDict()
    print('此时的Size为：', test_map.getSize())

输出结果：
初始字典Size： 0
初始字典是否为空： True
10次添加操作后：
Size: 10
是否包含7？ True
[Key: 9, Value: 9_index]–>[Key: 8, Value: 8_index]–>[Key: 7, Value: 7_index]–>[Key: 6, Value: 6_index]–>[Key: 5, Value: 5_index]–>[Key: 4, Value: 4_index]–>[Key: 3, Value: 3_index]–>[Key: 2, Value: 2_index]–>[Key: 1, Value: 1_index]–>[Key: 0, Value: 0_index]–>None
键为6的value： 6_index
将键值为4的value设为 “你好呀”,并打印：
[Key: 9, Value: 9_index]–>[Key: 8, Value: 8_index]–>[Key: 7, Value: 7_index]–>[Key: 6, Value: 6_index]–>[Key: 5, Value: 5_index]–>[Key: 4, Value: 你好呀]–>[Key: 3, Value: 3_index]–>[Key: 2, Value: 2_index]–>[Key: 1, Value: 1_index]–>[Key: 0, Value: 0_index]–>None
删除键为7的元素，并打印：
[Key: 9, Value: 9_index]–>[Key: 8, Value: 8_index]–>[Key: 6, Value: 6_index]–>[Key: 5, Value: 5_index]–>[Key: 4, Value: 你好呀]–>[Key: 3, Value: 3_index]–>[Key: 2, Value: 2_index]–>[Key: 1, Value: 1_index]–>[Key: 0, Value: 0_index]–>None
此时的Size为： 9

8 线性查找与二分查找

8.1 线性查找

线性查找就是从头找到尾，直到符合条件了就返回。比如在一个 list 中找到一个等于 5 的元素并返回下标：

number_list=[0,1,2,3,4,5]

def linear_search(value,iterable):
    for index,val in enumerate(iterable):
        if val==value:
            return index
    return -1


if __name__=="__main__":
    assert  linear_search(5, number_list) == 5

输出正常，

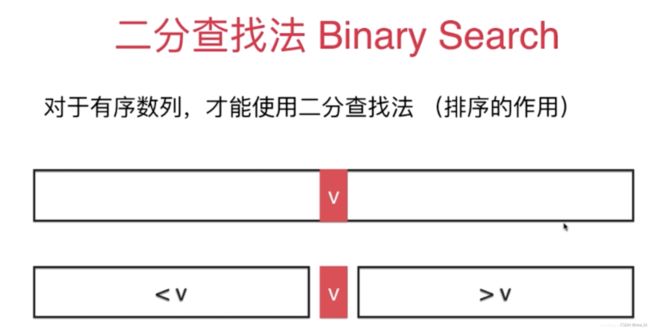
8.2 二分查找（有序数组）

非递归算法：

def binary_search(sorted_array, target):
    if not sorted_array:
        return -1
    beg = 0
    end = len(sorted_array) - 1
    while beg <= end:
        mid = (end + beg) // 2
        if sorted_array[mid] == target:
            return mid
        elif sorted_array[mid] > target:
            end = mid - 1
        elif sorted_array[mid] < target:
            beg = mid + 1
    return -1

if __name__ == "__main__":
    a = list(range(10))
    res = binary_search(a, 3)
    print(res)

递归实现：

def binary_search(sorted_array,low,high, target):
    if low>high:
        return -1
    mid = (low + high) // 2
    if sorted_array[mid] == target:
        return mid
    elif sorted_array[mid] > target:
        high = mid - 1
        return binary_search(sorted_array,low,high, target)
    else:
        low = mid + 1
        return binary_search(sorted_array, low, high, target)


if __name__ == "__main__":
    a = list(range(10))
    res = binary_search(a,0,len(a)-1, 3)
    print(res)

8.3 剑指Offer例题

8.3.1 两数之和 II - 输入有序数组给定一个已按照升序排列的有序数组，找到两个数使得它们相加之和等于目标数。

函数应该返回这两个下标值 index1 和 index2，其中 index1 必须小于 index2。
说明:
返回的下标值（index1 和 index2）是从零开始的。
你可以假设每个输入只对应唯一的答案，而且你不可以重复使用相同的元素。
示例:
输入: numbers = [2, 7, 11, 15], target = 9
输出: [1,2]
解释: 2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。

9 树和二叉树

9.1 树

线性结构中不论是数组还是链表，他们都存在着诟病；比如查找某个数必须从头开始查，消耗较多的时间。使用树结构，在插入和查找的性能上相对都会比线性结构要好。
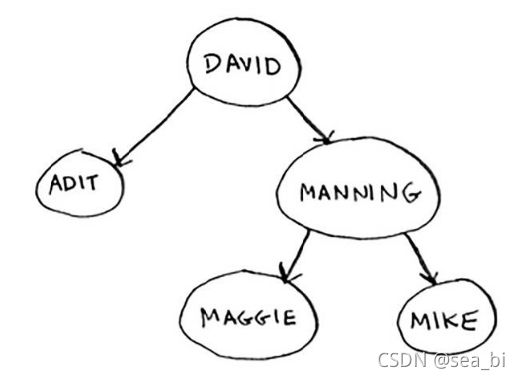
这里先简单讲讲树的概念。树结构是一种包括节点(nodes)和边(edges)的拥有层级关系的一种结构，它的形式和家谱树非常类似:

补充：
树的种类
无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树；
有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树；
二叉树：每个节点最多含有两个子树的树称为二叉树；
完全二叉树：对于一颗二叉树，假设其深度为d(d>1)。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树，其中满二叉树的定义是所有叶节点都在最底层的完全二叉树;
平衡二叉树（AVL树）：当且仅当任何节点的两棵子树的高度差不大于1的二叉树；
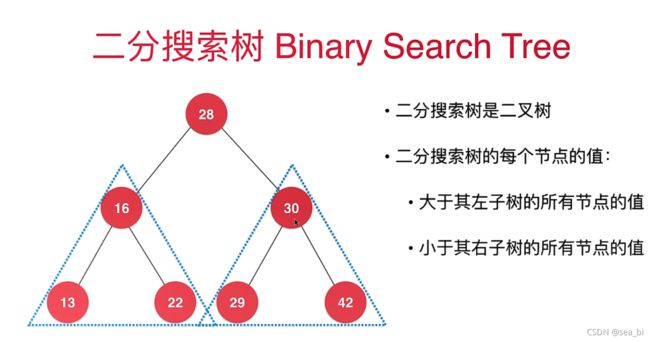
排序二叉树（二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树）；
霍夫曼树（用于信息编码）：带权路径最短的二叉树称为哈夫曼树或最优二叉树；
B树：一种对读写操作进行优化的自平衡的二叉查找树，能够保持数据有序，拥有多余两个子树。

9.2 二叉树

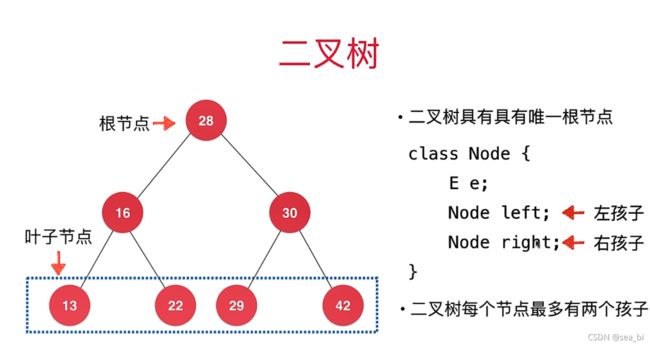
了解完树的结构以后，我们来看树结构里一种简单但是却比较常用的树-二叉树。二叉树是一种简单的树，它的每个节点最多只能包含两个孩子，以下都是一些合法的二叉树:

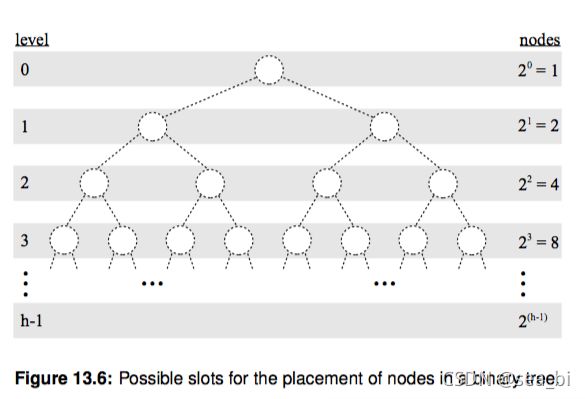
通过上边这幅图再来看几个二叉树相关的概念:
节点深度(depth): 节点对应的 level 数字。
1、树的高度(height): 二叉树的高度就是 level 数 + 1，因为 level 从 0开始计算的。
2、树的宽度(width): 二叉树的宽度指的是包含最多节点的层级的节点数
3、树的 size：二叉树的节点总个数。

二叉树的性质(特性)
性质1：在二叉树的第i层上至多有2^(i-1)个结点（i>0）

性质2：深度为k的二叉树至多有2^k - 1个结点（k>0）

性质3：对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1;

性质4：具有n个结点的完全二叉树的深度必为 log2(n+1)

性质5：对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号必为2i＋1；其双亲的编号必为i/2（i＝1 时为根,除外）

满二叉树与完全二叉树
满二叉树：所有叶子结点都集中在二叉树的最下面一层上，而且结点总数为：2^n-1 (n为层数 / 高度）

完全二叉树：所有的叶子节点都在最后一层或者倒数第二层，且最后一层叶子节点在左边连续，倒数第二层在右边连续（满二叉树也是属于完全二叉树）（从上往下，从左往右能挨着数满）

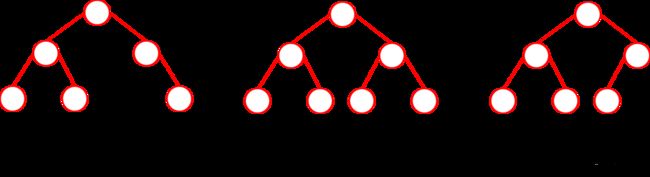
一棵 size 为 n 的二叉树高度最多可以是 n，最小的高度是 ⌊lgn⌋+1，这里 log 以 2 为底简写为 lgn，和算法导论保持一致。这个结果你只需要用高中的累加公式就可以得到。

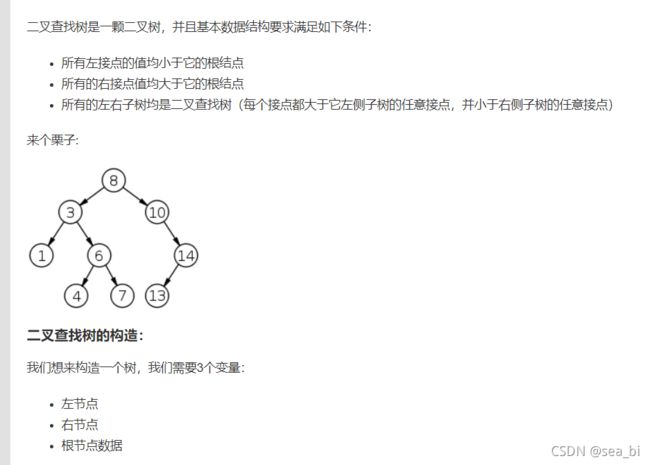
二叉树的遍历
二叉树其实是一种递归结构，因为单独拿出来一个 subtree 子树出来，其实它还是一棵树。那遍历它就很方便啦，我们可以直接用递归的方式来遍历它。但是当处理顺序不同的时候，树又分为三种遍历方式:
1、先(根)序遍历: 先处理根，之后是左子树，然后是右子树
2、中(根)序遍历: 先处理左子树，之后是根，最后是右子树
3、后(根)序遍历: 先处理左子树，之后是右子树，最后是根

9.2.1 先(根)序遍历

先序遍历：根节点，左节点，右节点（如果节点有子树，先从左往右遍历子树，再遍历兄弟节点）
先序遍历结果为：A B D H I E J C F K G

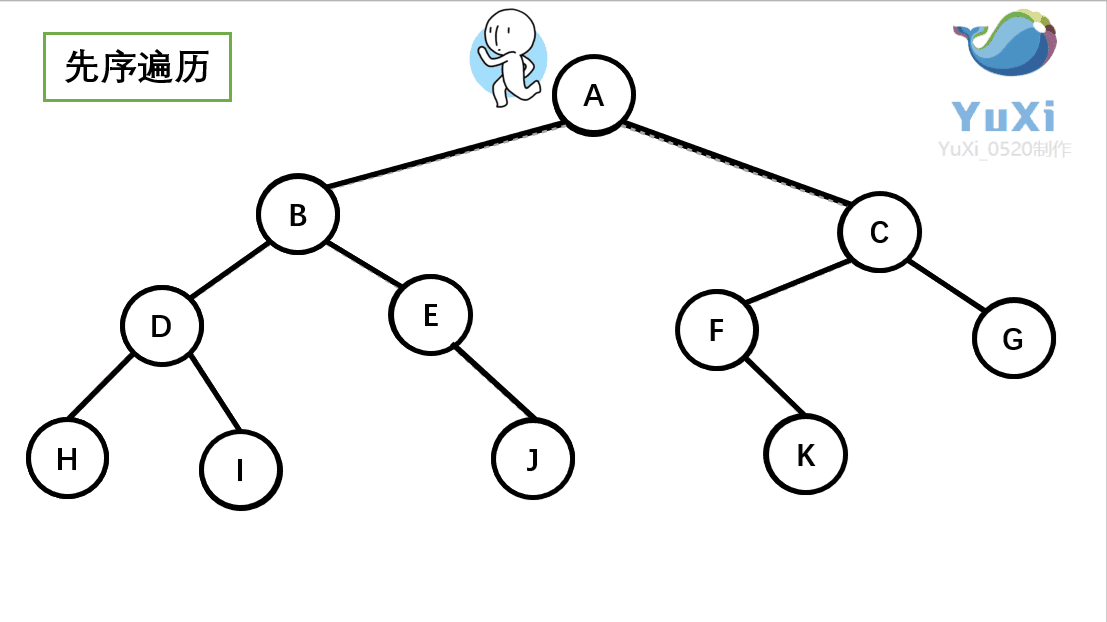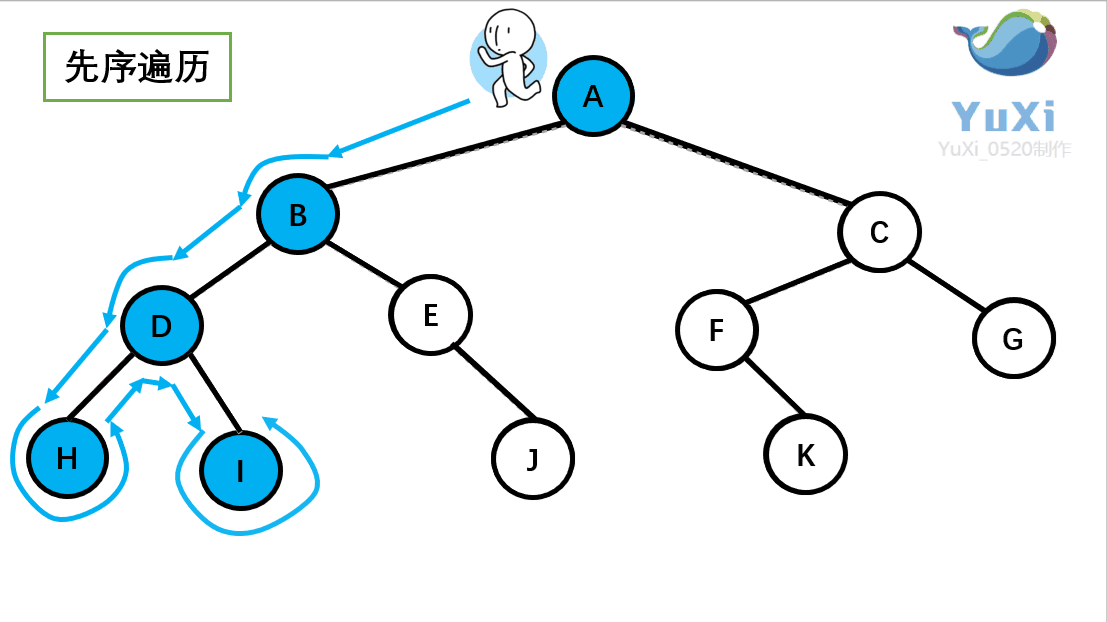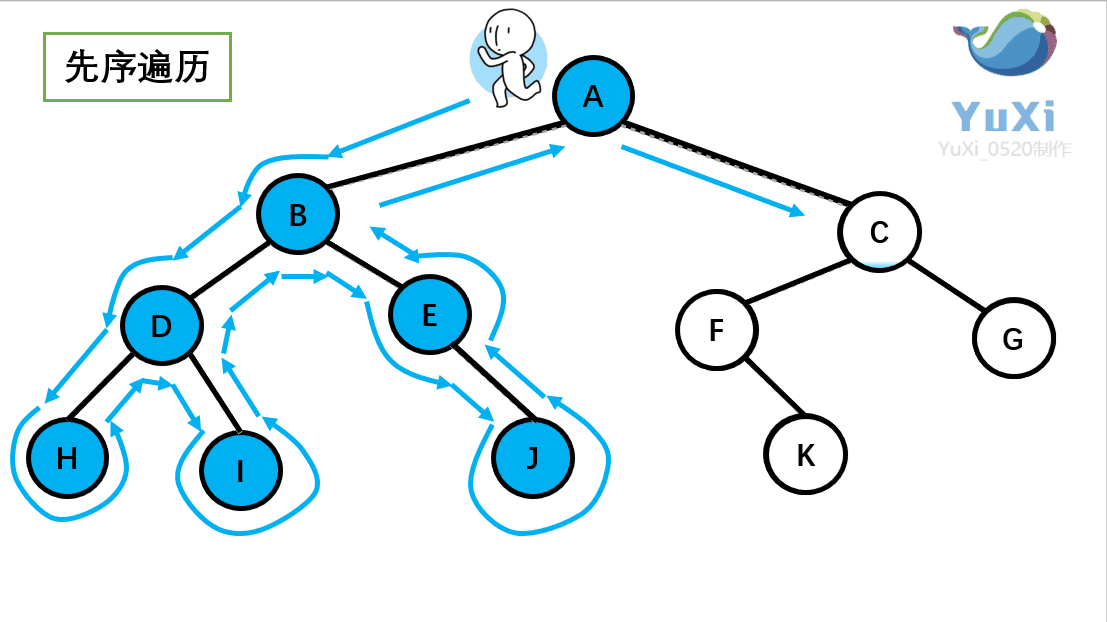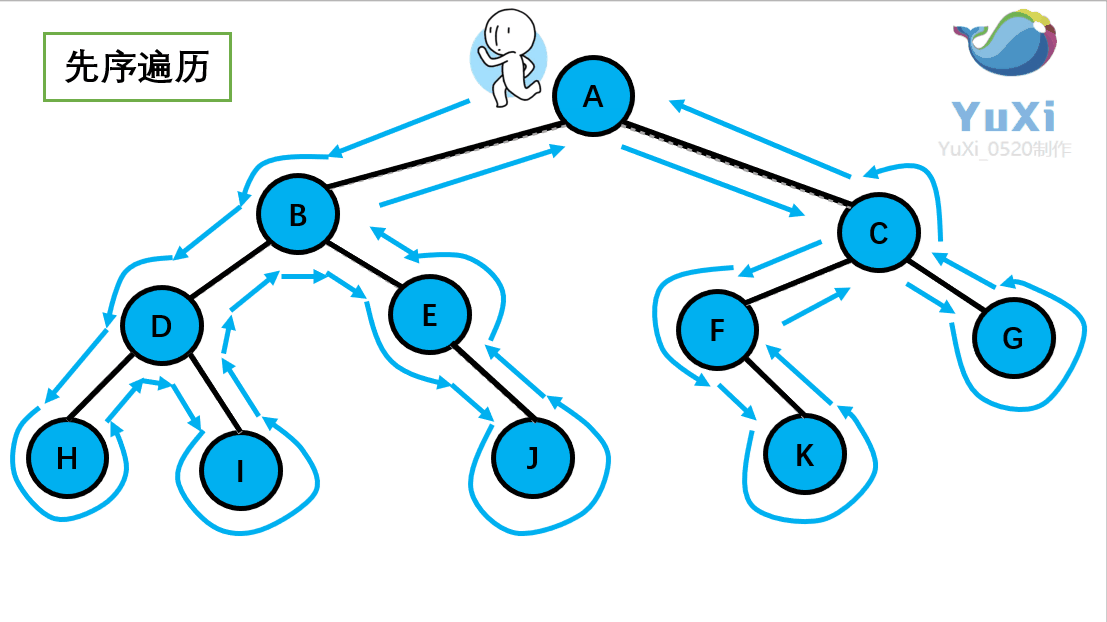
class Node:
    def __init__(self,elem):
        """
             节点构造函数，三个成员：携带的元素，指向左孩子的指针（标签），指向右孩子的指针（标签）
             :param elem: 携带的元素
        """
        self.elem=elem
        self.left=None # 左孩子设为空
        self.right=None  # 右孩子设为空

class BST:
    def __init__(self):
        """
        二分搜索树的构造函数——————空树
        """
        self._root = None       # 根节点设为None
        self._size = 0          # 有效元素个数初始化为0

    def __repr__(self):
        return '二分搜索树'

    def getSize(self):
        """
        返回节点个数
        :return: 节点个数
        """
        return self._size

    def isEmpty(self):
        """
                返回节点个数
                :return: 节点个数
        """
        return self._size==0


    def insert(self,data):
        """
                向二分搜索树插入元素elem
                时间复杂度：O(logn)
                :param elem: 待插入的元素
                :return: 二分搜索树的根
        """
        self._root = self._add(self._root, data)  # 调用私有函数self._add

    def _add(self,node,elem):
        """
             向以Node为根的二分搜索树插入元素elem，递归算法，这个根可以是任意节点哦，因为二分搜索树的每一个节点都是一个新的二分搜索树的根节点
             :param Node: 根节点
             :param elem: 带插入元素
             :return:     插入新节点后二分搜索树的根
         """
        if node is None:  # 递归到底的情况，此时已经到了None的位置。注意Node也算一棵二分搜索树
            self._size+=1
            return Node(elem)  # 新建一个携带elem的节点Node，并将它返回
        if node.elem>elem:
            node.left=self._add(node.left,elem)
        else:
            node.right=self._add(node.right,elem)

        return node  # 最后要把node返回，还是这个根，满足定义。

#二分搜索树的前序遍历
    def preOrfer(self):
        """
        二分搜索树的前序遍历
        时间复杂度：O(n)
        前序遍历、中序遍历以及后续遍历是针对当前的根节点来说的。前序就是把对根节点的操作放在遍历左、右子树的前面，
        相应的中序遍历以及后序遍历以此类推
        前序遍历是最自然也是最常用的二叉搜索树的遍历方式
        """
        self._preOrder(self._root)        # 调用self._preOrder函数

    def _preOrder(self,node):
        if node is None:
            return
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作
        self._preOrder(node.left)  # 再左子树
        self._preOrder(node.right)  # 再右子树



if __name__ == "__main__":
   test_bst=BST()
   print('初始大小：', test_bst.getSize())
   print('是否为空：', test_bst.isEmpty())

   add_list = [15, 4, 25, 22, 3, 19, 23, 7, 28, 24]
   print('待添加元素：', add_list)

   ##################################################
   #                    15                          #
   #               /           \                    #
   #               4           25                   #
   #            /      \     /    \                 #
   #           3        7    22    28               #
   #                        /   \                   #
   #                      19     23                 #
   #                               \                #
   #                                24              #
   ##################################################

   for add_elem in add_list:
       test_bst.insert(add_elem)
   print('前序遍历：（递归版本）')
   test_bst.preOrfer()

输出结果：
初始大小： 0
是否为空： True
待添加元素： [15, 4, 25, 22, 3, 19, 23, 7, 28, 24]
前序遍历：（递归版本）
15–>4–>3–>7–>25–>22–>19–>23–>24–>28–>

9.2.2 中序遍历

中序遍历：左节点，根节点，右节点（中序遍历可以看成，二叉树每个节点，垂直方向投影下来（可以理解为每个节点从最左边开始垂直掉到地上），然后从左往右数）
中遍历结果为：H D I B E J A F K C G

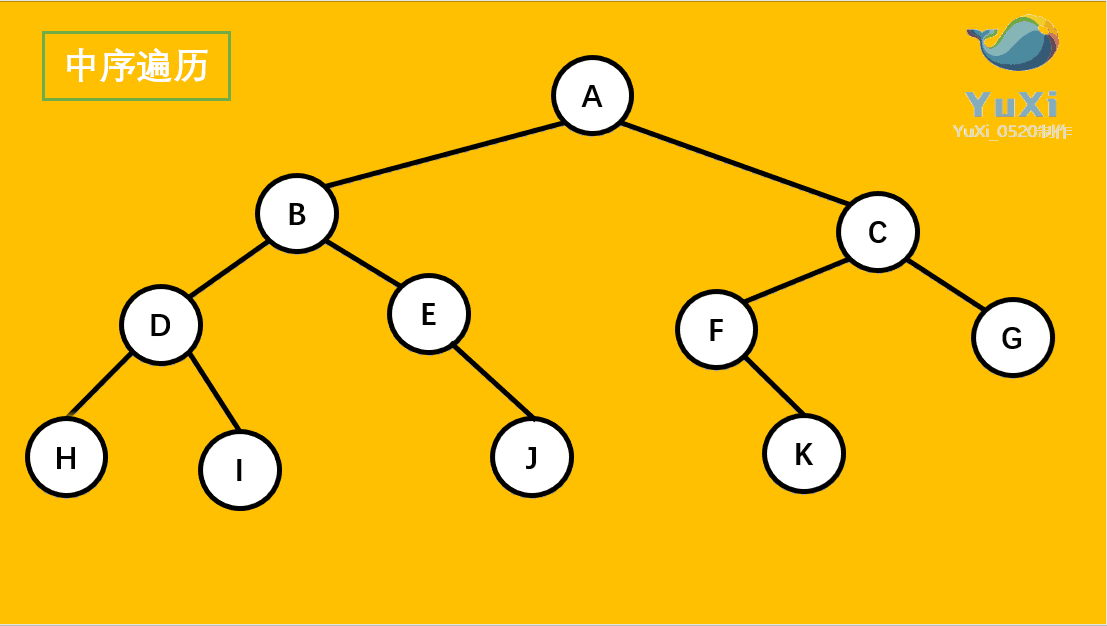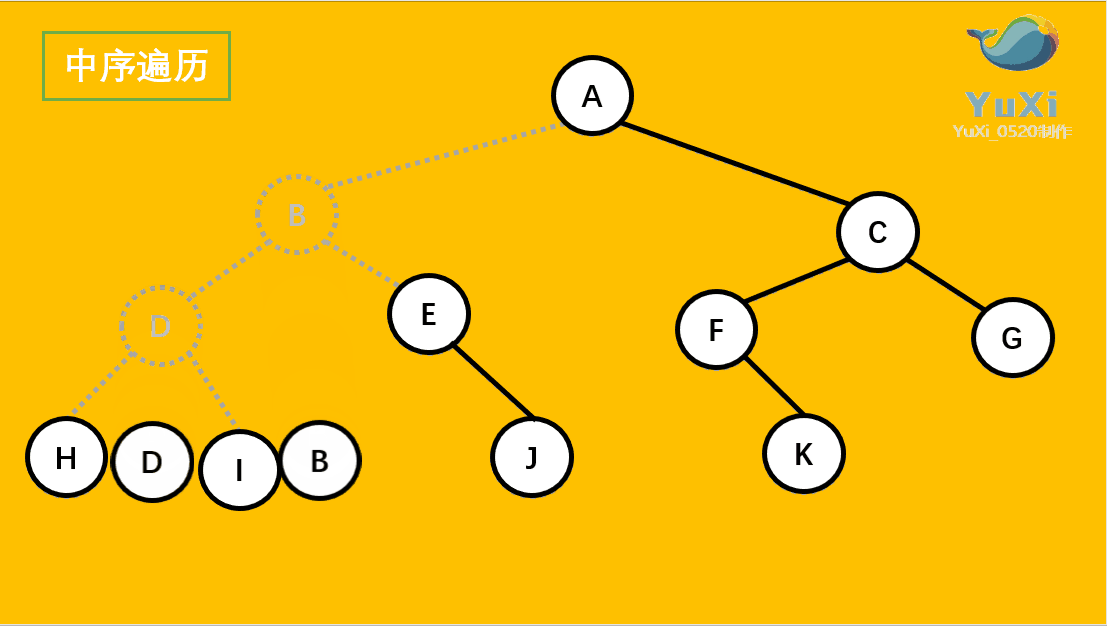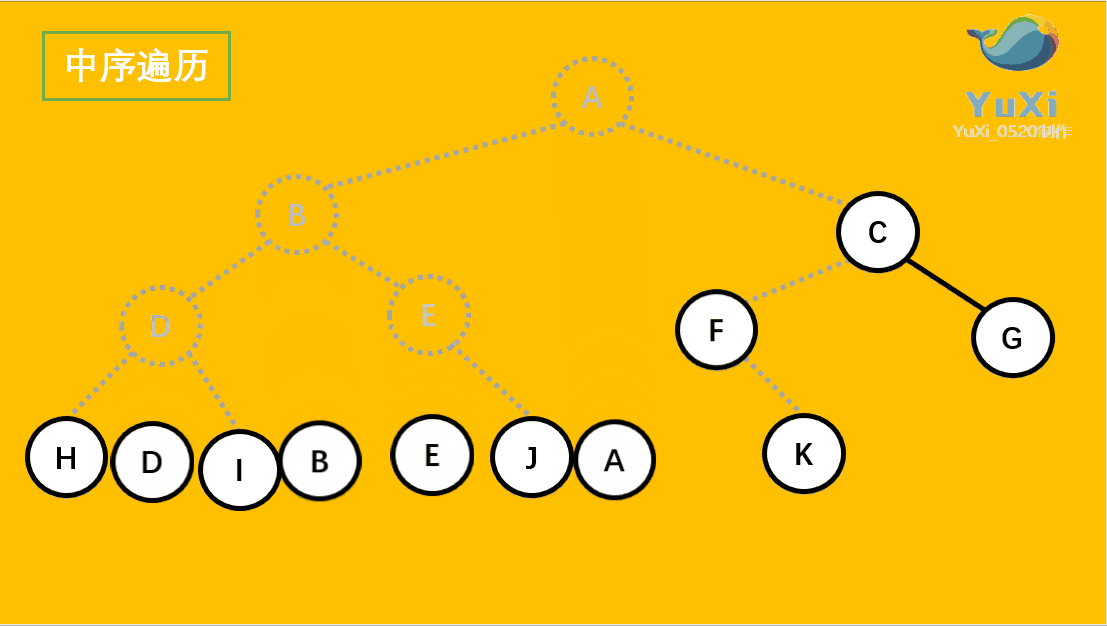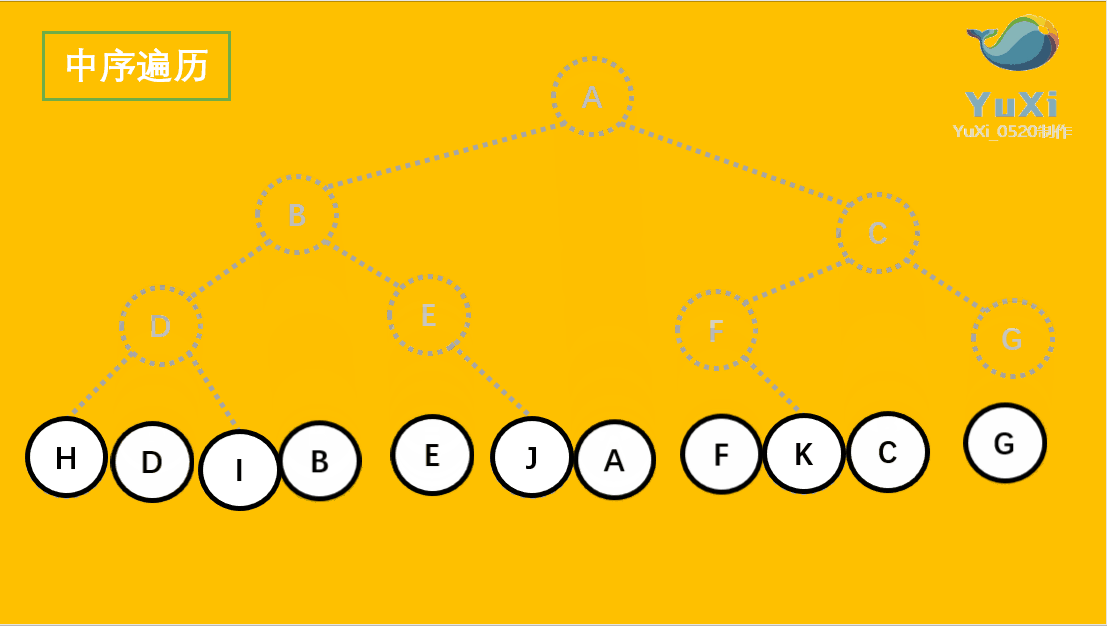
class Node:
    def __init__(self,elem):
        """
             节点构造函数，三个成员：携带的元素，指向左孩子的指针（标签），指向右孩子的指针（标签）
             :param elem: 携带的元素
        """
        self.elem=elem
        self.left=None # 左孩子设为空
        self.right=None  # 右孩子设为空


class BST:
    def __init__(self):
        """
        二分搜索树的构造函数——————空树
        """
        self._root = None       # 根节点设为None
        self._size = 0          # 有效元素个数初始化为0

    def __repr__(self):
        return '二分搜索树'

    def getSize(self):
        """
        返回节点个数
        :return: 节点个数
        """
        return self._size

    def isEmpty(self):
        """
                返回节点个数
                :return: 节点个数
        """
        return self._size==0


    def insert(self,data):
        """
                向二分搜索树插入元素elem
                时间复杂度：O(logn)
                :param elem: 待插入的元素
                :return: 二分搜索树的根
        """
        self._root = self._add(self._root, data)  # 调用私有函数self._add

    def _add(self,node,elem):
        """
             向以Node为根的二分搜索树插入元素elem，递归算法，这个根可以是任意节点哦，因为二分搜索树的每一个节点都是一个新的二分搜索树的根节点
             :param Node: 根节点
             :param elem: 带插入元素
             :return:     插入新节点后二分搜索树的根
         """
        if node is None:  # 递归到底的情况，此时已经到了None的位置。注意Node也算一棵二分搜索树
            self._size+=1
            return Node(elem)  # 新建一个携带elem的节点Node，并将它返回
        if node.elem>elem:
            node.left=self._add(node.left,elem)
        else:
            node.right=self._add(node.right,elem)

        return node  # 最后要把node返回，还是这个根，满足定义。


    def preOrfer(self):
        """
        二分搜索树的前序遍历
        时间复杂度：O(n)
        前序遍历、中序遍历以及后续遍历是针对当前的根节点来说的。前序就是把对根节点的操作放在遍历左、右子树的前面，
        相应的中序遍历以及后序遍历以此类推
        前序遍历是最自然也是最常用的二叉搜索树的遍历方式
        """
        self._preOrder(self._root)        # 调用self._preOrder函数

    def _preOrder(self,node):
        if node is None:
            return
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作
        self._preOrder(node.left)  # 再左子树
        self._preOrder(node.right)  # 再右子树

#二分搜索树的中序遍历
    def inOrder(self):
        """
        二分搜索树的中序遍历
        时间复杂度：O(n)
        特点：输出的元素是从小到大排列的，因为先处理左子树，到底后再处理当前节点，最后再处理右子树，而左子树的值都比当前节点小，
              右子树的值都比当前节点大，所以是排序输出
        """
        self._inOrder(self._root)  # 调用self._inOrder函数

    def _inOrder(self,node):
        if node is None:
            return
        self._inOrder(node.left)  # 再左子树
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作
        self._inOrder(node.right)  # 再右子树


if __name__ == "__main__":
   test_bst=BST()
   print('初始大小：', test_bst.getSize())
   print('是否为空：', test_bst.isEmpty())

   add_list = [15, 4, 25, 22, 3, 19, 23, 7, 28, 24]
   print('待添加元素：', add_list)

   ##################################################
   #                    15                          #
   #               /           \                    #
   #               4           25                   #
   #            /      \     /    \                 #
   #           3        7    22    28               #
   #                        /   \                   #
   #                      19     23                 #
   #                               \                #
   #                                24              #
   ##################################################

   for add_elem in add_list:
       test_bst.insert(add_elem)
   print('中序遍历：（递归版本）')
   test_bst.inOrder()

输出结果：
初始大小： 0
是否为空： True
待添加元素： [15, 4, 25, 22, 3, 19, 23, 7, 28, 24]
中序遍历：（递归版本）
3–>4–>7–>15–>19–>22–>23–>24–>25–>28–>

9.2.3 后序遍历

后序遍历：左节点，右节点，根节点
后序遍历结果：H I D J E B K F G C A

class Node:
    def __init__(self,elem):
        """
             节点构造函数，三个成员：携带的元素，指向左孩子的指针（标签），指向右孩子的指针（标签）
             :param elem: 携带的元素
        """
        self.elem=elem
        self.left=None # 左孩子设为空
        self.right=None  # 右孩子设为空


class BST:
    def __init__(self):
        """
        二分搜索树的构造函数——————空树
        """
        self._root = None       # 根节点设为None
        self._size = 0          # 有效元素个数初始化为0

    def __repr__(self):
        return '二分搜索树'

    def getSize(self):
        """
        返回节点个数
        :return: 节点个数
        """
        return self._size

    def isEmpty(self):
        """
                返回节点个数
                :return: 节点个数
        """
        return self._size==0


    def insert(self,data):
        """
                向二分搜索树插入元素elem
                时间复杂度：O(logn)
                :param elem: 待插入的元素
                :return: 二分搜索树的根
        """
        self._root = self._add(self._root, data)  # 调用私有函数self._add

    def _add(self,node,elem):
        """
             向以Node为根的二分搜索树插入元素elem，递归算法，这个根可以是任意节点哦，因为二分搜索树的每一个节点都是一个新的二分搜索树的根节点
             :param Node: 根节点
             :param elem: 带插入元素
             :return:     插入新节点后二分搜索树的根
         """
        if node is None:  # 递归到底的情况，此时已经到了None的位置。注意Node也算一棵二分搜索树
            self._size+=1
            return Node(elem)  # 新建一个携带elem的节点Node，并将它返回
        if node.elem>elem:
            node.left=self._add(node.left,elem)
        else:
            node.right=self._add(node.right,elem)

        return node  # 最后要把node返回，还是这个根，满足定义。


    def preOrfer(self):
        """
        二分搜索树的前序遍历
        时间复杂度：O(n)
        前序遍历、中序遍历以及后续遍历是针对当前的根节点来说的。前序就是把对根节点的操作放在遍历左、右子树的前面，
        相应的中序遍历以及后序遍历以此类推
        前序遍历是最自然也是最常用的二叉搜索树的遍历方式
        """
        self._preOrder(self._root)        # 调用self._preOrder函数

    def _preOrder(self,node):
        if node is None:
            return
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作
        self._preOrder(node.left)  # 再左子树
        self._preOrder(node.right)  # 再右子树

#二分搜索树的中序遍历
    def inOrder(self):
        """
        二分搜索树的中序遍历
        时间复杂度：O(n)
        特点：输出的元素是从小到大排列的，因为先处理左子树，到底后再处理当前节点，最后再处理右子树，而左子树的值都比当前节点小，
              右子树的值都比当前节点大，所以是排序输出
        """
        self._inOrder(self._root)  # 调用self._inOrder函数

    def _inOrder(self,node):
        if node is None:
            return
        self._inOrder(node.left)  # 再左子树
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作
        self._inOrder(node.right)  # 再右子树

    def postOrder(self):
        """
        二分搜索树的后序遍历
        应用场景：二叉搜索树的内存回收，例如C++中的析构函数
        时间复杂度：O(n)
        """
        self._postOrder(self._root)  # 调用self._postOrder函数

    def _postOrder(self, node):
        if node is None:
            return
        self._postOrder(node.left)  # 再左子树
        self._postOrder(node.right)  # 再右子树
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作

if __name__ == "__main__":
   test_bst=BST()
   print('初始大小：', test_bst.getSize())
   print('是否为空：', test_bst.isEmpty())

   add_list = [15, 4, 25, 22, 3, 19, 23, 7, 28, 24]
   print('待添加元素：', add_list)

   ##################################################
   #                    15                          #
   #               /           \                    #
   #               4           25                   #
   #            /      \     /    \                 #
   #           3        7    22    28               #
   #                        /   \                   #
   #                      19     23                 #
   #                               \                #
   #                                24              #
   ##################################################

   for add_elem in add_list:
       test_bst.insert(add_elem)
   print('后序遍历：（递归版本）')
   test_bst.postOrder()

输出结果：
初始大小： 0
是否为空： True
待添加元素： [15, 4, 25, 22, 3, 19, 23, 7, 28, 24]
后序遍历：（递归版本）
3–>7–>4–>19–>24–>23–>22–>28–>25–>15–>

9.2.4 包含关系

class Node:
    def __init__(self, elem):
        """
             节点构造函数，三个成员：携带的元素，指向左孩子的指针（标签），指向右孩子的指针（标签）
             :param elem: 携带的元素
        """
        self.elem = elem
        self.left = None  # 左孩子设为空
        self.right = None  # 右孩子设为空


class BST:
    def __init__(self):
        """
        二分搜索树的构造函数——————空树
        """
        self._root = None  # 根节点设为None
        self._size = 0  # 有效元素个数初始化为0

    def __repr__(self):
        return '二分搜索树'

    def getSize(self):
        """
        返回节点个数
        :return: 节点个数
        """
        return self._size

    def isEmpty(self):
        """
                返回节点个数
                :return: 节点个数
        """
        return self._size == 0

    def insert(self, data):
        """
                向二分搜索树插入元素elem
                时间复杂度：O(logn)
                :param elem: 待插入的元素
                :return: 二分搜索树的根
        """
        self._root = self._add(self._root, data)  # 调用私有函数self._add

    def _add(self, node, elem):
        """
             向以Node为根的二分搜索树插入元素elem，递归算法，这个根可以是任意节点哦，因为二分搜索树的每一个节点都是一个新的二分搜索树的根节点
             :param Node: 根节点
             :param elem: 带插入元素
             :return:     插入新节点后二分搜索树的根
         """
        if node is None:  # 递归到底的情况，此时已经到了None的位置。注意Node也算一棵二分搜索树
            self._size += 1
            return Node(elem)  # 新建一个携带elem的节点Node，并将它返回
        if node.elem > elem:
            node.left = self._add(node.left, elem)
        else:
            node.right = self._add(node.right, elem)

        return node  # 最后要把node返回，还是这个根，满足定义。

    def preOrfer(self):
        """
        二分搜索树的前序遍历
        时间复杂度：O(n)
        前序遍历、中序遍历以及后续遍历是针对当前的根节点来说的。前序就是把对根节点的操作放在遍历左、右子树的前面，
        相应的中序遍历以及后序遍历以此类推
        前序遍历是最自然也是最常用的二叉搜索树的遍历方式
        """
        self._preOrder(self._root)  # 调用self._preOrder函数

    def _preOrder(self, node):
        if node is None:
            return
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作
        self._preOrder(node.left)  # 再左子树
        self._preOrder(node.right)  # 再右子树

    # 二分搜索树的中序遍历
    def inOrder(self):
        """
        二分搜索树的中序遍历
        时间复杂度：O(n)
        特点：输出的元素是从小到大排列的，因为先处理左子树，到底后再处理当前节点，最后再处理右子树，而左子树的值都比当前节点小，
              右子树的值都比当前节点大，所以是排序输出
        """
        self._inOrder(self._root)  # 调用self._inOrder函数

    def _inOrder(self, node):
        if node is None:
            return
        self._inOrder(node.left)  # 再左子树
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作
        self._inOrder(node.right)  # 再右子树

    def postOrder(self):
        """
        二分搜索树的后序遍历
        应用场景：二叉搜索树的内存回收，例如C++中的析构函数
        时间复杂度：O(n)
        """
        self._postOrder(self._root)  # 调用self._postOrder函数

    def _postOrder(self, node):
        if node is None:
            return
        self._postOrder(node.left)  # 再左子树
        self._postOrder(node.right)  # 再右子树
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作

    # 查看二分搜索树中是否包含elem
    def contain(self, elem):
        """
               查看二分搜索树中是否包含elem
               时间复杂度：O(logn)
               :param elem: 待查询元素
               :return:     bool值，查到为True
        """
        return self._contains(self._root, elem)

    def _contains(self, node, elem):
        if node is None:
            return False
        if node.elem < elem:
            return self._contains(node.right, elem)
        elif node.elem > elem:
            return self._contains(node.left, elem)
        else:
            return True


if __name__ == "__main__":
    test_bst = BST()
    print('初始大小：', test_bst.getSize())
    print('是否为空：', test_bst.isEmpty())

    add_list = [15, 4, 25, 22, 3, 19, 23, 7, 28, 24]
    print('待添加元素：', add_list)

    ##################################################
    #                    15                          #
    #               /           \                    #
    #               4           25                   #
    #            /      \     /    \                 #
    #           3        7    22    28               #
    #                        /   \                   #
    #                      19     23                 #
    #                               \                #
    #                                24              #
    ##################################################

    for add_elem in add_list:
        test_bst.insert(add_elem)
    print('后序遍历：（递归版本）')
    test_bst.postOrder()
    print("\n")
    print("是否包含28？", test_bst.contain(28))

是否包含28？ True

9.2.5 前序遍历的非递归写法

class Node:
    def __init__(self, elem):
        """
             节点构造函数，三个成员：携带的元素，指向左孩子的指针（标签），指向右孩子的指针（标签）
             :param elem: 携带的元素
        """
        self.elem = elem
        self.left = None  # 左孩子设为空
        self.right = None  # 右孩子设为空


class BST:
    def __init__(self):
        """
        二分搜索树的构造函数——————空树
        """
        self._root = None  # 根节点设为None
        self._size = 0  # 有效元素个数初始化为0

    def __repr__(self):
        return '二分搜索树'

    def getSize(self):
        """
        返回节点个数
        :return: 节点个数
        """
        return self._size

    def isEmpty(self):
        """
                返回节点个数
                :return: 节点个数
        """
        return self._size == 0

    def insert(self, data):
        """
                向二分搜索树插入元素elem
                时间复杂度：O(logn)
                :param elem: 待插入的元素
                :return: 二分搜索树的根
        """
        self._root = self._add(self._root, data)  # 调用私有函数self._add

    def _add(self, node, elem):
        """
             向以Node为根的二分搜索树插入元素elem，递归算法，这个根可以是任意节点哦，因为二分搜索树的每一个节点都是一个新的二分搜索树的根节点
             :param Node: 根节点
             :param elem: 带插入元素
             :return:     插入新节点后二分搜索树的根
         """
        if node is None:  # 递归到底的情况，此时已经到了None的位置。注意Node也算一棵二分搜索树
            self._size += 1
            return Node(elem)  # 新建一个携带elem的节点Node，并将它返回
        if node.elem > elem:
            node.left = self._add(node.left, elem)
        else:
            node.right = self._add(node.right, elem)

        return node  # 最后要把node返回，还是这个根，满足定义。

    def preOrfer(self):
        """
        二分搜索树的前序遍历
        时间复杂度：O(n)
        前序遍历、中序遍历以及后续遍历是针对当前的根节点来说的。前序就是把对根节点的操作放在遍历左、右子树的前面，
        相应的中序遍历以及后序遍历以此类推
        前序遍历是最自然也是最常用的二叉搜索树的遍历方式
        """
        self._preOrder(self._root)  # 调用self._preOrder函数

    def _preOrder(self, node):
        if node is None:
            return
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作
        self._preOrder(node.left)  # 再左子树
        self._preOrder(node.right)  # 再右子树

    # 二分搜索树的中序遍历
    def inOrder(self):
        """
        二分搜索树的中序遍历
        时间复杂度：O(n)
        特点：输出的元素是从小到大排列的，因为先处理左子树，到底后再处理当前节点，最后再处理右子树，而左子树的值都比当前节点小，
              右子树的值都比当前节点大，所以是排序输出
        """
        self._inOrder(self._root)  # 调用self._inOrder函数

    def _inOrder(self, node):
        if node is None:
            return
        self._inOrder(node.left)  # 再左子树
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作
        self._inOrder(node.right)  # 再右子树

    def postOrder(self):
        """
        二分搜索树的后序遍历
        应用场景：二叉搜索树的内存回收，例如C++中的析构函数
        时间复杂度：O(n)
        """
        self._postOrder(self._root)  # 调用self._postOrder函数

    def _postOrder(self, node):
        if node is None:
            return
        self._postOrder(node.left)  # 再左子树
        self._postOrder(node.right)  # 再右子树
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作

    # 查看二分搜索树中是否包含elem
    def contain(self, elem):
        """
               查看二分搜索树中是否包含elem
               时间复杂度：O(logn)
               :param elem: 待查询元素
               :return:     bool值，查到为True
        """
        return self._contains(self._root, elem)

    def _contains(self, node, elem):
        if node is None:
            return False
        if node.elem < elem:
            return self._contains(node.right, elem)
        elif node.elem > elem:
            return self._contains(node.left, elem)
        else:
            return True

    #前序遍历的非递归写法
    def preOrderNR(self):
        """
               前序遍历的非递归写法
               此时需要借助一个辅助的数据结构————栈
               时间复杂度：O(n)
               空间复杂度：O(n)
               技巧：压栈的时候先右孩子，再左孩子，从而左孩子先出栈。
        """
        self._preOrderNR(self._root)

    def _preOrderNR(self,node):
        """
               对以node为根节点的二叉搜索树的非递归的前序遍历
               :param node: 当前根节点
        """
        stack = ArrayStack()  # 初始化一个我们以前实现的栈

        if node:
            stack.push(node)  # 如果根节点不为空，就首先入栈
        else:
            return
        while not stack.isEmpty():  # 栈始终不为空
            ret = stack.pop()  # 出栈并拿到栈顶的节点
            print(ret.elem, end='-->')  # 打印（我这里就只选择打印操作了，当然可以对这个节点执行任何你想要的操作）
            if ret.right:  # 出栈后，看一下ret的左右孩子，先入右孩子
                stack.push(ret.right)
            if ret.left:  # 再入栈左孩子，想想为什么是先右后左
                stack.push(ret.left)

class ArrayStack:
    def __init__(self):
        self.intems=[]
    def isEmpty(self):
        return self.intems==[]
    def push(self,item):
        return self.intems.append(item)
    def pop(self):
        return self.intems.pop()






if __name__ == "__main__":
    test_bst = BST()
    print('初始大小：', test_bst.getSize())
    print('是否为空：', test_bst.isEmpty())

    add_list = [15, 4, 25, 22, 3, 19, 23, 7, 28, 24]
    print('待添加元素：', add_list)

    ##################################################
    #                    15                          #
    #               /           \                    #
    #               4           25                   #
    #            /      \     /    \                 #
    #           3        7    22    28               #
    #                        /   \                   #
    #                      19     23                 #
    #                               \                #
    #                                24              #
    ##################################################

    for add_elem in add_list:
        test_bst.insert(add_elem)
    print('前序遍历：（递归版本）')
    test_bst.preOrfer()
    print("\n")
    print('前序遍历：（非递归版本）')
    test_bst.preOrderNR()

前序遍历：（非递归版本）
15–>4–>3–>7–>25–>22–>19–>23–>24–>28–>

通过上述比较，两种方法都返回同样的结果。

9.2.6 广度优先/深度优先遍历二叉树

广度优先(层次遍历)
广度优先遍历，又称广度优先搜索，缩写BFS,广度优先和深度优先是两种常用的遍历图的方法。如果说深度优先遍历是相当于树的前序遍历，那么，广度优先遍历就相当于树的层序遍历。
以一个树状图来说，广度优先就是从根节点开始，一层一层的遍历，下一层的必须等上一层全部遍历完成才可以被访问。而以一个无向图来举例的话，通过下面的图来理解：

S为起点
接下来遍历位于同一层次的A,B,C
再接下来遍历下一层次的D
数和二叉树的区别就是，二叉树只有左右两个节点
所以顺序为S,A,B,C,D。

层次遍历：从上往下，从左往右
层次遍历结果：A B C D E F G H I J K

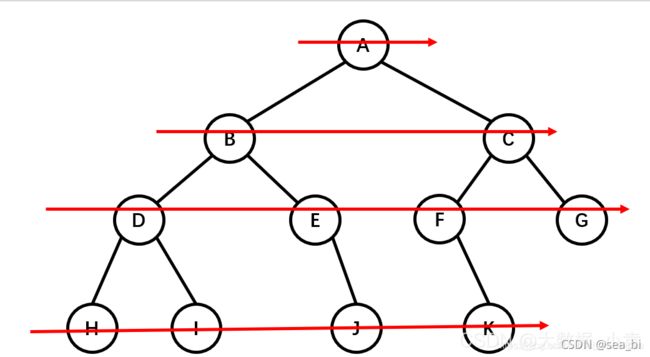
深度优先

深度优先有三种算法：前序遍历，中序遍历，后序遍历

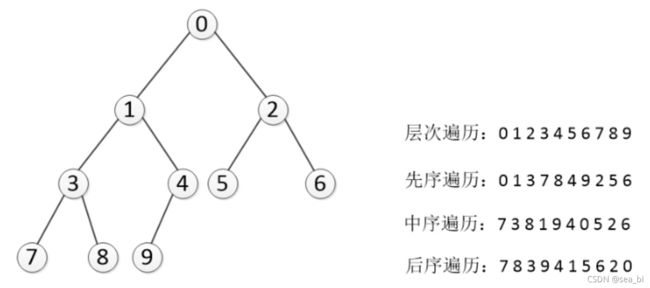
先序遍历在先序遍历中，我们先访问根节点，然后递归使用先序遍历访问左子树，再递归使用先序遍历访问右子树


# 广度优先/深度优先遍历二叉树

class Node:
    def __init__(self, data, left, right):
        self._data = data
        self._left = left
        self._right = right

class BinaryTree:
    def __init__(self):
        self._root = None

    def make_tree(self, node):
        self._root = node

    def insert(self, node):
        # 这里是建立一个完全二叉树
        lst = []
        def insert_node(tree_node, p, node):
            if tree_node._left is None:
                tree_node._left = node
                lst.append(tree_node._left)
                return
            elif tree_node._right is None:
                tree_node._right = node
                lst.append(tree_node._right)
                return
            else:
                lst.append(tree_node._left)
                lst.append(tree_node._right)
                if p > (len(lst) -2):
                    return
                else:
                    insert_node(lst[p+1], p+1, node)


        lst.append(self._root)
        insert_node(self._root, 0, node)

def breadth_tree(tree):
    lst = []

    def traverse(node, p):
        if node._left is not None:
            lst.append(node._left)
        if node._right is not None:
            lst.append(node._right)
        if p > (len(lst) -2):
            return
        else:
            traverse(lst[p+1], p+1)

    lst.append(tree._root)
    traverse(tree._root, 0)

    # 遍历结果就存在了lst表里
    for node in lst:
        print(node._data,end=",")

def depth_tree(tree):
    lst = []
    lst.append(tree._root)
    while len(lst) > 0:
        node = lst.pop()
        print(node._data,end=",")
        if node._right is not None:
            lst.append(node._right)
        if node._left is not None:
            lst.append(node._left)

if __name__ == '__main__':
    lst = [12, 9, 7, 19, 3, 8, 52, 106, 70, 29, 20, 16, 8, 50, 22, 19]
    tree = BinaryTree()
    # 生成完全二叉树
    for (i, j) in enumerate(lst):
        node = Node(j, None, None)
        if i == 0:
            tree.make_tree(node)
        else:
            tree.insert(node)

    # 广度优先遍历
    breadth_tree(tree)
    print("\n")
    # 深度优先遍历
    depth_tree(tree)

输出结果：
** 广度优先遍历**
12,9,7,19,3,8,52,106,70,29,20,16,8,50,22,19,
深度优先遍历
12,9,19,106,19,70,3,29,20,7,8,16,8,52,50,22,

9.2.7 查找最大值、最小值

class Node:
    def __init__(self, elem):
        """
             节点构造函数，三个成员：携带的元素，指向左孩子的指针（标签），指向右孩子的指针（标签）
             :param elem: 携带的元素
        """
        self.elem = elem
        self.left = None  # 左孩子设为空
        self.right = None  # 右孩子设为空


class BST:
    def __init__(self):
        """
        二分搜索树的构造函数——————空树
        """
        self._root = None  # 根节点设为None
        self._size = 0  # 有效元素个数初始化为0

    def __repr__(self):
        return '二分搜索树'

    def getSize(self):
        """
        返回节点个数
        :return: 节点个数
        """
        return self._size

    def isEmpty(self):
        """
                返回节点个数
                :return: 节点个数
        """
        return self._size == 0

    def insert(self, data):
        """
                向二分搜索树插入元素elem
                时间复杂度：O(logn)
                :param elem: 待插入的元素
                :return: 二分搜索树的根
        """
        self._root = self._add(self._root, data)  # 调用私有函数self._add

    def _add(self, node, elem):
        """
             向以Node为根的二分搜索树插入元素elem，递归算法，这个根可以是任意节点哦，因为二分搜索树的每一个节点都是一个新的二分搜索树的根节点
             :param Node: 根节点
             :param elem: 带插入元素
             :return:     插入新节点后二分搜索树的根
         """
        if node is None:  # 递归到底的情况，此时已经到了None的位置。注意Node也算一棵二分搜索树
            self._size += 1
            return Node(elem)  # 新建一个携带elem的节点Node，并将它返回
        if node.elem > elem:
            node.left = self._add(node.left, elem)
        else:
            node.right = self._add(node.right, elem)

        return node  # 最后要把node返回，还是这个根，满足定义。

    def preOrfer(self):
        """
        二分搜索树的前序遍历
        时间复杂度：O(n)
        前序遍历、中序遍历以及后续遍历是针对当前的根节点来说的。前序就是把对根节点的操作放在遍历左、右子树的前面，
        相应的中序遍历以及后序遍历以此类推
        前序遍历是最自然也是最常用的二叉搜索树的遍历方式
        """
        self._preOrder(self._root)  # 调用self._preOrder函数

    def _preOrder(self, node):
        if node is None:
            return
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作
        self._preOrder(node.left)  # 再左子树
        self._preOrder(node.right)  # 再右子树

    # 二分搜索树的中序遍历
    def inOrder(self):
        """
        二分搜索树的中序遍历
        时间复杂度：O(n)
        特点：输出的元素是从小到大排列的，因为先处理左子树，到底后再处理当前节点，最后再处理右子树，而左子树的值都比当前节点小，
              右子树的值都比当前节点大，所以是排序输出
        """
        self._inOrder(self._root)  # 调用self._inOrder函数

    def _inOrder(self, node):
        if node is None:
            return
        self._inOrder(node.left)  # 再左子树
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作
        self._inOrder(node.right)  # 再右子树

    def postOrder(self):
        """
        二分搜索树的后序遍历
        应用场景：二叉搜索树的内存回收，例如C++中的析构函数
        时间复杂度：O(n)
        """
        self._postOrder(self._root)  # 调用self._postOrder函数

    def _postOrder(self, node):
        if node is None:
            return
        self._postOrder(node.left)  # 再左子树
        self._postOrder(node.right)  # 再右子树
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作

    # 查看二分搜索树中是否包含elem
    def contain(self, elem):
        """
               查看二分搜索树中是否包含elem
               时间复杂度：O(logn)
               :param elem: 待查询元素
               :return:     bool值，查到为True
        """
        return self._contains(self._root, elem)

    def _contains(self, node, elem):
        if node is None:
            return False
        if node.elem < elem:
            return self._contains(node.right, elem)
        elif node.elem > elem:
            return self._contains(node.left, elem)
        else:
            return True

    #前序遍历的非递归写法
    def preOrderNR(self):
        """
               前序遍历的非递归写法
               此时需要借助一个辅助的数据结构————栈
               时间复杂度：O(n)
               空间复杂度：O(n)
               技巧：压栈的时候先右孩子，再左孩子，从而左孩子先出栈。
        """
        self._preOrderNR(self._root)

    def _preOrderNR(self,node):
        """
               对以node为根节点的二叉搜索树的非递归的前序遍历
               :param node: 当前根节点
        """
        stack = ArrayStack()  # 初始化一个我们以前实现的栈

        if node:
            stack.push(node)  # 如果根节点不为空，就首先入栈
        else:
            return
        while not stack.isEmpty():  # 栈始终不为空
            ret = stack.pop()  # 出栈并拿到栈顶的节点
            print(ret.elem, end='-->')  # 打印（我这里就只选择打印操作了，当然可以对这个节点执行任何你想要的操作）
            if ret.right:  # 出栈后，看一下ret的左右孩子，先入右孩子
                stack.push(ret.right)
            if ret.left:  # 再入栈左孩子，想想为什么是先右后左
                stack.push(ret.left)

    def minimum(self):
        """
        Description: 返回当前二叉搜索树的最小值
        时间复杂度：O(n)
        """
        if self._size == 0:  # 空树直接报错
            raise Exception('Empty binary search tree!')
        return self._minimum(self._root).elem  # 调用self._minimum函数，它传入当前的根节点

    def _minimum(self, node):
        """
        Description: 返回以node为根的二叉搜索树携带最小值的节点
        """
        if node.left is None:  # 递归到底的情况，二叉搜索树的最小值就从当前节点一直向左孩子查找就好了
            return node
        return self._minimum(node.left)  # 否则向该节点的左子树继续查找


    def maximum(self):
        """
        Description: 返回当前二叉搜索树的最大值
        时间复杂度：O(logn)
        """
        if self._size == 0:  # 空树直接报错
            raise Exception('Empty binary search tree!')
        return self._maximum(self._root).elem  # 调用self._maxmum函数，它传入当前的根节点

    def _maximum(self, node):
        """
        Description: 返回以node为根的二叉搜索树携带最大值的节点
        """
        if node.right is None:  # 递归到底的情况，二叉搜索树的最大值就从当前节点一直向右孩子查找就好了
            return node
        return self._maximum(node.right)  # 否则向该节点的右子树继续查找


class ArrayStack:
    def __init__(self):
        self.intems=[]
    def isEmpty(self):
        return self.intems==[]
    def push(self,item):
        return self.intems.append(item)
    def pop(self):
        return self.intems.pop()


if __name__ == "__main__":
    test_bst = BST()
    print('初始大小：', test_bst.getSize())
    print('是否为空：', test_bst.isEmpty())

    add_list = [15, 4, 25, 22, 3, 19, 23, 7, 28, 24]
    print('待添加元素：', add_list)
    for add_elem in add_list:
        test_bst.insert(add_elem)

    ##################################################
    #                    15                          #
    #               /           \                    #
    #               4           25                   #
    #            /      \     /    \                 #
    #           3        7    22    28               #
    #                        /   \                   #
    #                      19     23                 #
    #                               \                #
    #                                24              #
    ##################################################

    print('树中最小值：', test_bst.minimum())
    print('树中最大值：', test_bst.maximum())

输出结果：
初始大小： 0
是否为空： True
待添加元素： [15, 4, 25, 22, 3, 19, 23, 7, 28, 24]
树中最小值： 3
树中最大值： 28

9.3 二叉排序树（Binary Sort Tree）

无序序列：

二叉排序树图解：

概述：二叉排序树（Binary Sort Tree）也叫二叉查找树或者是一颗空树，对于二叉树中的任何一个非叶子节点，要求左子节点比当前节点值小，右子节点比当前节点值大

特点：
1、查找性能与插入删除性能都适中还不错
2、中序遍历的结果刚好是从大到小
3、创建二叉排序树原理：其实就是不断地插入节点，然后进行比较。

删除节点
1、删除叶子节点，只需要找到父节点，将父节点与他的连接断开即可
2、删除有一个子节点的就需要将他的子节点换到他现在的位置
3、删除有两个子节点的节点，需要使用他的前驱节点或者后继节点进行替换，就是左子树最右下方的数（最大的那个）或右子树最左边的树（最小的数）；即离节点值最接近的值；（还要注解要去判断这个值有没有右节点，有就要将右节点移上来）

class Node:
    def __init__(self,elem):
        """
             节点构造函数，三个成员：携带的元素，指向左孩子的指针（标签），指向右孩子的指针（标签）
             :param elem: 携带的元素
        """
        self.elem=elem
        self.left=None # 左孩子设为空
        self.right=None  # 右孩子设为空


class BinarySortTree:
    def __init__(self):
        """
        二分搜索树的构造函数——————空树
        """
        self._root = None       # 根节点设为None
        self._size = 0          # 有效元素个数初始化为0

    def __repr__(self):
        return '二分排序树'

    def getSize(self):
        """
        返回节点个数
        :return: 节点个数
        """
        return self._size

    def isEmpty(self):
        """
                返回节点个数
                :return: 节点个数
        """
        return self._size==0


    def insert(self,data):
        """
                向二分搜索树插入元素elem
                时间复杂度：O(logn)
                :param elem: 待插入的元素
                :return: 二分搜索树的根
        """
        self._root = self._add(self._root, data)  # 调用私有函数self._add

    def _add(self,node,elem):
        """
             向以Node为根的二分搜索树插入元素elem，递归算法，这个根可以是任意节点哦，因为二分搜索树的每一个节点都是一个新的二分搜索树的根节点
             :param Node: 根节点
             :param elem: 带插入元素
             :return:     插入新节点后二分搜索树的根
         """
        if node is None:  # 递归到底的情况，此时已经到了None的位置。注意Node也算一棵二分搜索树
            self._size+=1
            return Node(elem)  # 新建一个携带elem的节点Node，并将它返回
        if node.elem>elem:
            node.left=self._add(node.left,elem)
        else:
            node.right=self._add(node.right,elem)

        return node  # 最后要把node返回，还是这个根，满足定义。


    #二分搜索树的中序遍历
    def inOrder(self):
        """
        二分搜索树的中序遍历
        时间复杂度：O(n)
        特点：输出的元素是从小到大排列的，因为先处理左子树，到底后再处理当前节点，最后再处理右子树，而左子树的值都比当前节点小，
              右子树的值都比当前节点大，所以是排序输出
        """
        self._inOrder(self._root)  # 调用self._inOrder函数

    def _inOrder(self,node):
        if node is None:
            return
        self._inOrder(node.left)  # 再左子树
        print(node.elem, end='-->')  # 在这里我只是对当前节点进行了打印操作，并没有什么别的操作
        self._inOrder(node.right)  # 再右子树


if __name__ == "__main__":
   test_bst=BinarySortTree()
   print('初始大小：', test_bst.getSize())
   print('是否为空：', test_bst.isEmpty())

   add_list = [15, 4, 25, 22, 3, 19, 23, 7, 28, 24]
   print('待添加元素：', add_list)

   ##################################################
   #                    15                          #
   #               /           \                    #
   #               4           25                   #
   #            /      \     /    \                 #
   #           3        7    22    28               #
   #                        /   \                   #
   #                      19     23                 #
   #                               \                #
   #                                24              #
   ##################################################

   for add_elem in add_list:
       test_bst.insert(add_elem)
   print('排序后输出：')
   test_bst.inOrder()

输出结果：
初始大小： 0
是否为空： True
待添加元素： [15, 4, 25, 22, 3, 19, 23, 7, 28, 24]
排序后输出：
3–>4–>7–>15–>19–>22–>23–>24–>25–>28–>

顺序已经排序好了。

9.4 平衡二叉树（ Balanced Binary Tree）

为什么使用平衡二叉树？
平衡二叉树（Balanced Binary Tree）又被称为AVL树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

…

https://blog.csdn.net/yuan2019035055/article/details/120576372

9.5 剑指Offer例题

9.5.1 【剑指Offer】4、重建二叉树

题目描述：
输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回根结点。

思路：首先二叉树先序（前序）遍历的顺序是：根–左--右。意思是先返回根，然后返回左子树，左子树返回后再返回右子树。每个子树的遍历顺序也是根–左--右。
二叉树的中序遍历顺序是左–根--右。
以前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}为例。
前序：{1,2,4,7,3,5,6,8}，按照根左右顺序，根节点是1。
中序：{4,7,2,1,5,3,8,6}，按照左根右顺序，根节点1左边{4,7,2}是左子树，根节点右边{5,3,8,6}是右子树。
按照这个思路，我们可以把根节点，左子树，右子树区分开来。那么对于左子树，重复刚刚的过程，就又可以得到左子树对应的根节点，以及左子树对应的左右子树。这就是传说中的递归解法！！把左子树丢到函数里，就能得到左子树的根节点和对应的左右子树！！但是递归要注意终止条件：
1、如果只有一个元素了，就把该元素返回；
2、如果没有元素了，返回None。
最后这棵树长这样：

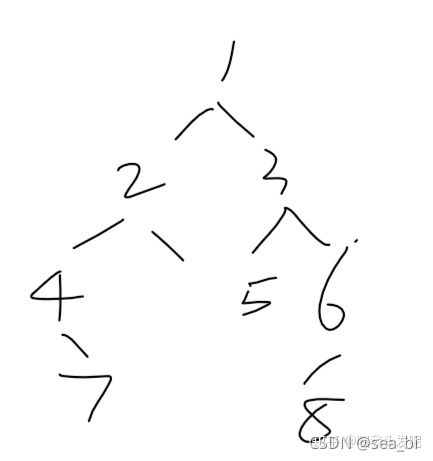
树的遍历有三种：分别是前序遍历、中序遍历、后序遍历。本题是根据前序和中序遍历序列重建二叉树，我们可以通过一个具体的实例来发现规律，不难发现：前序遍历序列的第一个数字就是树的根结点。在中序遍历序列中，可以扫描找到根结点的值，则左子树的结点都位于根结点的左边，右子树的结点都位于根结点的右边。
这样，我们就通过这两个序列找到了树的根结点、左子树结点和右子树结点，接下来左右子树的构建可以进一步通过递归来实现。

class TreeNode:
    def __init__(self,x):
        self.val=x
        self.right=None
        self.left=None

class Soultion:
    # 根据前序遍历和中序遍历确定一棵二叉树
    def reConstructBinaryTree(self, pre, tin):
        if len(pre)==1:
            return TreeNode(pre[0])
        if len(pre)==0:
            return None
        root=TreeNode(pre[0])
        index=tin.index(pre[0])
        root.left = self.reConstructBinaryTree(pre[1:index + 1], tin[0:index])
        root.right = self.reConstructBinaryTree(pre[index + 1:], tin[index + 1:])
        return root


if __name__ == "__main__":
    pre_list=[1,2,4,7,3,5,6,8]
    tin_list=[4,7,2,1,5,3,8,6]
    s=Soultion()
    res=s.reConstructBinaryTree(pre_list,tin_list)
    # 返回重构的二叉树
    print(res)

输出：

9.5.2 【剑指Offer】17、树的子结构

题目描述：
输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构）

思路：
我们可以把这个问题拆成两部分，一个是判断B是A的子树，一个是判断A有B这颗子树。
判断B是A的子树情况就是：从根节点下去，A的左右节点和B的左右节点都一样都一样。
这种情况的停止条件就是，
B的每一个节点都搜索完毕，且都和A一致，这样就可以停止。返回True
B还有没搜索完毕的，但是A已经空了，返回False


class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None


class Solution:
    # 以R为根的子树是否包含和树B相同的结构
    def isSubtree(self, a, b):
        if not b:
            return True
        if not a:
            return False
        if a.val != b.val:
            return False
        return self.isSubtree(a.left, b.left) and self.isSubtree(a.right, b.right)

    def HasSubtree(self, pRoot1, pRoot2):
        # write code here

        if not pRoot2 or not pRoot1:
            return False
        res = False
        #  有相同的根节点，判断第二步
        if pRoot2.val == pRoot1.val:
            res = self.isSubtree(pRoot1, pRoot2)
        # 不满足，继续在子树中查找
        if not res:
            res = self.isSubtree(pRoot1.left, pRoot2)
        # 左子树也没有找到，右子树查找
        if not res:
            res = self.isSubtree(pRoot1.right, pRoot2)

        return res

当然还有人写的代码是：

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None
class Solution:
    def isSubtree(self, a, b):
            if not b: 
                return True
            if not a:
                return False
            if a.val != b.val :
                return False
            return self.isSubtree(a.left, b.left) and self.isSubtree(a.right, b.right)
    def HasSubtree(self, pRoot1, pRoot2):
        # write code here
        if not pRoot2 or not pRoot1:
            return False
        return self.isSubtree(pRoot1, pRoot2) or self.isSubtree(pRoot1.left, pRoot2) or self.isSubtree(pRoot1.right, pRoot2)

9.5.3 【剑指Offer】18.二叉树的镜像

题目描述：
操作给定的二叉树，将其变换为原二叉树的镜像。

解题思路：
求一棵树的镜像的过程：先前序遍历这棵树的每个结点，如果遍历到的结点有子结点，就交换它的两个子结点。当交换完所有的非叶结点的左、右子结点后，就可以得到该树的镜像。
如下面的例子，先交换根节点的两个子结点之后，我们注意到值为10、6的结点的子结点仍然保持不变，因此我们还需要交换这两个结点的左右子结点。做完这两次交换之后，我们已经遍历完所有的非叶结点。此时变换之后的树刚好就是原始树的镜像。

这题递归

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution:
    # 返回镜像树的根节点
    def Mirror(self, root):
        if root == None:
            return root
        tmp = root.left
        root.left = root.right
        root.right = tmp
        # root.left,root.right =root.right,root.left 
        root.left = self.Mirror(root.left)
        root.right = self.Mirror(root.right)
        return root

那么今天的更新就到这里啦~明天再见！

9.5.4 【剑指Offer】22、从上往下打印二叉树

题目描述：

从上往下打印出二叉树的每个节点，同层节点从左至右打印。

解题思路：

本题实际上就是二叉树的层次遍历，深度遍历可以用递归或者栈，而层次遍历很明显应该使用队列。同样我们可以通过一个例子来分析得到规律：每次打印一个结点时，如果该结点有子结点，则将子结点放到队列的末尾，接下来取出队列的头重复前面的打印动作，直到队列中所有的结点都打印完毕。

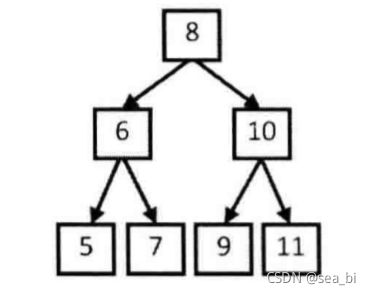
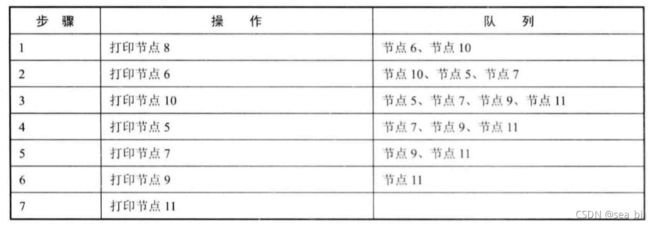
更直观的是
那么从实现上来讲，可以用nodes列表存储当前节点，模拟队列先入先出，另一个res列表存储打印结果。把每一层的节点都放到nodes当中，并且当遍历到当前节点时，将节点值存到res中。如果当前节点有左or右子节点，就将左or右子节点放到nodes队列尾部。

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
class Solution:
    # 返回从上到下每个节点值列表，例：[1,2,3]
    def PrintFromTopToBottom(self, root):
        if not root:
            return []
        nodes=[root]
        res=[]
        while nodes:
            cur=nodes.pop(0)
            res.append(cur.val)
            if cur.left:
                nodes.append(cur.left)
            if cur.right:
                nodes.append(cur.right)
        return res



if __name__ == "__main__":
    l1=TreeNode(1)
    l2 = TreeNode(2)
    l3 = TreeNode(3)
    l4 = TreeNode(4)
    l1.left=l2
    l1.right=l3
    l2.left=l4
    s=Solution()
    t=s.PrintFromTopToBottom(l1)
    print(t)

输出：
[1, 2, 3, 4]

9.5.5 【剑指Offer】23.二叉搜索树的后序遍历序列

题目描述：

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

解题思路：

对于后续遍历序列，序列的最后一个值一定是树的根结点，而由二叉搜索树的性质：左小右大，我们可以从头开始遍历，当遍历到某个值比根结点大时停止，记为flag，此时flag之前的所有数值都是二叉搜索树的左子树的结点，flag以及flag之后的所有数都是二叉搜索树的右子树的结点。这是由二叉搜索树以及后序遍历共同决定的。

接下来，我们就可以把任务交给递归，同样的方法去判断左子树和右子树是否是二叉搜索树，这显然是典型的递归解法。

举例：
以{5,7,6,9,11,10,8}为例，后序遍历结果的最后一个数字8就是根结点的值。在这个数组中，前3个数字5、7和6都比8小，是值为8的结点的左子树结点；后3个数字9、11和10都比8大，是值为8的结点的右子树结点。
我们接下来用同样的方法确定与数组每一部分对应的子树的结构。这其实就是一个递归的过程。对于序列5、7、6，最后一个数字6是左子树的根结点的值。数字5比6小，是值为6的结点的左子结点，而7则是它的右子结点。同样，在序列9、11、10中，最后一个数字10是右子树的根结点，数字9比10小，是值为10的结点的左子结点，而11则是它的右子结点，所以它对应的二叉搜索树如下：

例如：
[4,8,6,12,16,14,10]
当序列seq的长度为0，空树，不是二叉搜索树；
用i代表左右子树的index划分点，seq[0:i] 代表左子树， seq[i, -1]代表右子树， seq[-1]代表根节点；根据前一段子序列，值都比最后一个元素（根）小这个性质，找到i；
再根据后一段子序列，值都比最后一个元素大这个性质，判断一下是否要进行递归，如果满足这个性质的话：
判断左子树是否为二叉搜索树，前提是左子树存在，即 i>0，至少存在一个元素；
判断右子树是否为二叉搜索树，前提是右子树存在，即 i< len(seq) -1，至少存在一个元素；

class Solution:
    def VerifySquenceOfBST(self, seq):
        if len(seq) == 0:
            return False
        i = 0
        while seq[i] < seq[-1]:
            i += 1
        j = i
        for j in range(i, len(seq)):
            if seq[j] < seq[-1]:
                return False
        left = True
        if i > 0:
            left = self.VerifySquenceOfBST(seq[0:i])
        right = True
        if i < len(seq) - 1:
            right = self.VerifySquenceOfBST(seq[i: -1])
        return left and right

if __name__ == "__main__":
    s=Solution()
    t=s.VerifySquenceOfBST([4,8,6,12,16,14,10])
    print(t)

输出：
True

9.5.6 【剑指Offer】 24、二叉树中和为某一值的路径

题目描述：

输入一颗二叉树的根结点和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中，数组长度大的数组靠前)

解题思路：
本题实质上就是深度优先搜索。使用前序遍历的方式对整棵树进行遍历，当访问到某一个结点时，将该结点添加到路径上，并且累加该结点的值。当访问到的结点是叶结点时，如果路径中的结点值之和正好等于输入的整数，则说明是一条符合要求的路径。如果当前结点不是叶结点，则继续访问它的子结点。
当找到一条符合要求的路径之后，需要回溯进一步查找别的路径，因此，这实际上仍然是一个递归的过程，特别注意在函数返回之前要删掉当前结点，从而才可以正确的回溯。

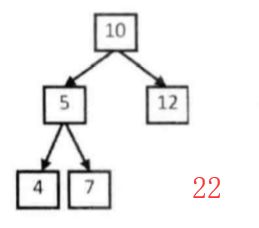
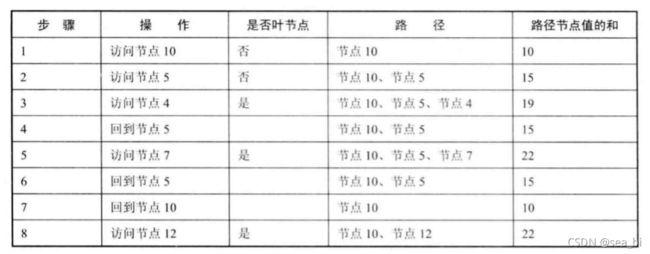
用list0存储当前路径， list1存储结果；
root是空的时候，直接返回空list结果；
list0先把root节点加入当前路径，然后让expectNumvber = expectNumvber - root.val，更新expectNumvber值；
这个时候判断一下是不是终止条件：expectNumer==0而且当且是叶子节点，如果满足终止条件，且找到了这样一条路径的话，把该条路径的结果存储到list1中；
如果不满足的话，list0里面已经有root了，expectNumer也变成了expectNumer-root.val，这个时候就在左右子树中找有没有满足expectNumer的序列即可~奇妙的递归出现了！
最后，划重点，不管有没有找到这样一条路径，都需要将当前节点pop出去，回溯到当前节点的父节点，再找有没有符合条件的路径~
实现：

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

class Solution:
    def __init__(self):
        # 用list0存储当前路径， list1存储结果；
        self.list0=[]
        self.list1=[]

    def FindPath(self,root,expectNumber):
        if not root:
            return self.list1
        self.list0.append(root.val)
        expectNumber-=root.val
        if expectNumber == 0 and not root.left and not root.right:  # 找到这样一条路径
            tmp = []  # 存结果到list1中
            for item in self.list0:
                tmp.append(item)
            self.list1.append(tmp)
        self.FindPath(root.left, expectNumber)
        self.FindPath(root.right, expectNumber)
        self.list0.pop()
        return self.list1



if __name__ == "__main__":
    l1 = TreeNode(1)
    l2 = TreeNode(2)
    l3 = TreeNode(3)
    l4 = TreeNode(4)
    l1.left = l2
    l1.right = l3
    l2.left = l4
    s=Solution()
    t=s.FindPath(l1,4)
    print(t)

输出：
[[1, 3]]

感觉这类题目都可以用递归进行求解。

10 集合基础与集合实现

集合(set)基础与集合实现
一、集合基础和基于二分搜索树的集合实现
集合：承载元素的容器，但每个元素都只能存在一次；能够快速实现“去重”这个工作；

（二分搜索树不能添加重复元素，是非常好的实现“集合”的底层数据结构）

基础功能代码：

Set

void add(E) :向集合中添加元素E（不能添加重复元素）

void remove(E) :从集合中删除元素E

boolean contains(E):检验集合是否包含元素E

int getSize:获取集合中元素的个数

boolean isEmpty():检验集合是否为空

基于二分搜索树实现集合（查重）

11 递归和循环

11.1 剑指Offer例题

11.1.1 【剑指Offer】7、斐波那契数列

题目描述：
大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。假设n<=39。
解题思路：
斐波那契数列：0,1,1,2,3,5,8… 总结起来就是：第一项是0，第二项是1，后续第n项为第n-1项和第n-2项之和。

用公式描述如下：

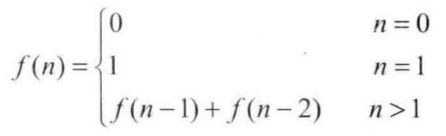
看到这个公式，非常自然的可以想到直接用递归解决。但是这里存在一个效率问题，以求f(10)为例，需要先求出前两项f(9)和f(8)，同样求f(9)的时候又需要求一次f(8)，这样会导致很多重复计算，下图可以直观的看出。重复计算的结点数会随着n的增加而急剧增加，导致严重的效率问题。

因此，可以不使用递归，直接使用简单的循环方法实现。

方法1：暴力递归法

class Solution:
    def Fibonacci(self, n):
        # write code here
        if n == 0:
            return 0
        if n == 1 :
            return 1
        else:
            return self.Fibonacci(n-2) + self.Fibonacci(n-1)

但是这种代码重复的计算增大了时间复杂度！

方法2：数组存储法

class Solution:
    def Fibonacci(self, n):
        res = [0,1,1,2] # res用于存储斐波那契数列前n项
        while len(res) <= n: # 如果第n项不在这个序列中 de 时候
            res.append(res[-1] + res[-2]) # 不断求前面的每一项，存到res里，直到n项也求出来
        return res[n]

if __name__=="__main__":
    s=Solution()
    res=s.Fibonacci(7)
    print(res)

输出：13

方法3：俩数存储法（迭代）
这里用两个数，a和b表示斐波那契数列的相邻两项，a在前b在后，while的每一次循环都更新a和b的值，直到更新到第n项。

class Solution:
    def Fibonacci(self, n):
        # write code here
        if n == 0:
            return 0
        if n == 1:
            return 1
        a, b = 0, 1
        while n > 1:
            a, b = b, a+b
            n -= 1
        return b

方法4：
直接使用简单的循环方法实现。

class Solution:
    def Fibonacci(self, n):
        if n==0:
            return 0
        if n==1:
            return 1
        first=0
        second=1
        res=0
        for i in range(2,n+1):
            res=first+second
            first=second
            second=res
        return res

if __name__=="__main__":
    s=Solution()
    res=s.Fibonacci(7)
    print(res)

输出：13

11.1.2 【剑指Offer】8、跳台阶

题目描述：
一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。
解题思路：
首先考虑最简单的情况，如果只有1级台阶，显然只有一种跳法。如果有两级台阶，就有两种跳法：一种是分两次跳，一种是一次跳两级。
在一般情况下，可以把n级台阶的跳法看成n的函数，记为f(n)，那么一般情况下，一开始我们有两种不同的选择：（1）第一步只跳一级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目，即f(n-1)；（2）第一步跳两级，那么跳法数目等于后面剩下的n-2级台阶的跳法数目，即f(n-2)。所以f(n)=f(n-1)+f(n-2)。
至此，我们不难看出本题实际上就是求斐波那契数列，直接按照第7题思路便可以解决。

假设只有1个台阶，那就跳1个，只有一种方法, f(1) = 1；
假设只有2个台阶，那就跳1个2次，或者2个1次，有两种方法 f(2) = 2；
假设只有3个台阶，如果就跳1个，剩下两个台阶，跳法数是f(3-1)。如果跳2个，剩下1个台阶，跳法数是f(3-2)；
假设有n个台阶，如果先跳1个，就会剩下f(n-1)个跳法，如果先跳2个，就会剩下f(n-2)个跳法，所以f(n) = f(n-1)+f(n-2)！
激动的心颤抖的手，这就是斐波那契数列换了层皮啊！！需要注意一点，这个台阶有n个，而n势必大于1，由于f(1)=1, f(2)=2，可以看出数列是从第3项开始计算的~ Fib = [0,1,1,2,…]
上面的代码随便挑一种方法就可以啦~

方法1：

class Solution:
    def Fibonacci(self, n):
        if n==0:
            return 0
        if n==1:
            return 1
        if n == 2:
            return 2
        first=1
        second=2
        res=0
        for i in range(3,n+1):
            res=first+second
            first=second
            second=res
        return res

if __name__=="__main__":
    s=Solution()
    res=s.Fibonacci(7)
    print(res)

其他方法参考上一题。

11.1.3 【剑指Offer】9、变态跳台阶

题目描述：
一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
解题思路：
当只有一级台阶时，f(1)=1；
当有两级台阶时，f(2)=f(2-1)+f(2-2)；
一般情况下，当有n级台阶时，f(n)=f(n-1)+f(n-2)+···+f(n-n)=f(0)+f(1)+···+f(n-1)，同理，f(n-1)=f(0)+f(1)+···+f(n-2).
因此，根据上述规律可以得到：f(n)=2*f(n-1)。这时一个递推公式，同样为了效率问题，用循环可以实现。
这是个等比数列，首项是1，公比是2.，所以an=2^(n-1)

解法1：

class Solution:
    def jumpFloorII(self, number):
        # write code here
        return pow(2,number-1)

解法2：

class Solution:
    def JumpFloorII(self, n):
        if n==0:
            return 0
        if n==1:
            return 1
        res=1
        i=2
        while i<=n:
            res=res*2
            i+=1
        return res


if __name__=="__main__":
    s=Solution()
    res=s.JumpFloorII(3)
    print(res)

解法3：递归解法

class Solution:
    def JumpFloorII(self, n):
        if n<0:
            return 0
        if n==1:
            return 1
        return self.JumpFloorII(n-1)*2


if __name__=="__main__":
    s=Solution()
    res=s.JumpFloorII(4)
    print(res)

有一个讲解拨云见日：除了最后一个台阶一定要站上去，从1到n-1个台阶都可以选择跳or不跳，所以一共有2^(n-1)种跳法。

11.1.4 【剑指Offer】10、矩形覆盖

题目描述：
我们可以用2 X 1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2 X 1的小矩形无重叠地覆盖一个2 X n的大矩形，总共有多少种方法？
解题思路：
我们可以以2 X 8的矩形为例，这题主要是识别是斐波那契数列变形。

先把2X8的覆盖方法记为f(8)，用1X2的小矩形去覆盖时，有两种选择：横着放或者竖着放。当竖着放时，右边还剩下2X7的区域。很明显这种情况下覆盖方法为f(7)。当横着放时，1X2的矩形放在左上角，其下方区域只能也横着放一个矩形，此时右边区域值剩下2X6的区域，这种情况下覆盖方法为f(6)。所以可以得到：f(8)=f(7)+f(6)，不难看出这仍然是斐波那契数列。
特殊情况：f(1)=1，f(2)=2
当n=3时，2*3的矩形块有3种覆盖方法:

def rectCover(self, n):
        # write code here
        if n == 0:
            return 0
        if n == 1:
            return 1
        if n == 2:
            return 2
        else:
            a , b = 1,2
            while n > 2:
                a, b = b , a+b
                n -= 1
            return b

基本都是斐波那契数列，解法参考前面几题。

12 其他

12.1 剑指Offer例题

12.1.1【剑指Offer】11、二进制中1的个数

题目描述：
输入一个整数，输出该数二进制表示中1的个数。其中负数用补码表示。

解题思路：
第一种，简单粗暴的解法是转换成str，再用str的count找有几个1。分两种情况，分别是n>=0和n<0。
n>=0，正常计算；
n<0，由于计算补码，n=n+2^32。

class Solution:
    def NumberOf1(self, n):
        if n>=0:
            s = str(bin(n)).count('1') # s是1的个数
        if n==1:
            s = str(bin(pow(2,32)+n)).count('1')
        return s


if __name__=="__main__":
    s=Solution()
    res=s.NumberOf1(4)
    print(res)

解法二:
另一种解法是比较巧妙的，能够体现编程之美的，剑指offer给出的解答~
假设该数n不为0，那么至少有1个1，不管这个1的位置在哪里，用n-1的话，n最右边的1变为0，最右边1后面所有的0变为1，其余位不变。然后如果把n和n-1做与运算，最右边的1就没有啦！！
废话不多说，上图示！

这样减了两次1之后，就没有1了！全是0！结果1的个数就是2个~

class Solution:
    def NumberOf1( self, n):
        if n == 0:
            return 0
        res = 0
        if n <= 0:
            n += pow(2,32)
        while n:
            n &= (n-1)
            res += 1
        return res

12.1.2【剑指Offer】12、数值的整数次方

题目描述：
给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。

解法1：求base的exponent次方

class Solution:
    def Power(self, base, exponent):
        return pow(base, exponent)

当然了，面试的时候这么回答，可能坟头草都2米了

class Solution:
    def Power(self, base, exponent):
        if base == 0:
            return 0
        if exponent == 0:
            return 1
        res = 1
        for i in range(abs(exponent)):
           res *= base
        if exponent < 0:
           return 1/res
        else:
            return res

算法和数据结构