第五课.可变图结构下的归纳式学习&图注意力
目录
- 图采样聚合网络
-
- Inductive and Transductive Learning
- GraphSAGE
- 算法流程
- GraphSAGE与InductiveLearning的关系
- 损失函数
- 注意力机制简介
- 图注意力网络
-
- GAT
- GaAN
图采样聚合网络
Inductive and Transductive Learning
Inductive Learning 直译为归纳式学习,归纳是从观察到的训练案例学习到一般规则,然后应用到测试用例中;归纳式学习定义为从现有数据中学习知识,然后把知识用于以前从没见过的数据上,比如图像识别,语义分割,目标检测等模型的训练,在训练集上训练,然后在从以前未见过的验证集上评估,就是归纳学习;
Transductive Learning 直译为直推式学习,Transductive 是从观察到的、具体的(训练)案例到具体的(测试)案例的学习;之前接触的大部分GNN模型都属于直推式学习;
归纳式学习与人们通常所说的传统监督学习是一样的,我们基于我们已经拥有的标记训练数据集建立和训练机器学习模型,然后我们使用这个训练好的模型来预测我们以前从未遇到过的测试数据集的标签;直推式学习技术对所有数据进行了事先观察,无论是训练数据还是测试数据,我们从已经观察到的训练数据集中学习,然后预测测试数据集的标签,即使我们不知道测试数据集的标签,我们也可以在学习过程中使用数据呈现的模式和附加信息;
一般GNN的学习都是 Transductive Learning,以Cora数据集为例,每个节点代表一篇论文,一共2708个节点,如果两篇论文间有引用关系,则两个节点之间有边相连接,对于节点的特征,从所有论文中提取出1433个常用的高频词,然后在每篇论文中对比,出现过就在该高频词对应的位置记为1,否则记为0;对于Cora,可以有两种任务:节点分类,或者节点间是否有边的预测;
- 假设现在的任务是 Link Prediction,我们可以人为地遮挡数据集中的一些连接边关系,因此目前模型可以看到整个数据下的节点类别和特征,以及部分连接关系,剩下要做的是让模型学习可以看到的信息,再预测哪些节点之间应该有边连接,哪些不应该有;
- 如果任务为节点分类,则遮挡部分节点的类别,模型可以看到整个数据的边连接关系,和所有节点的特征以及部分节点的类别;
特别地,GNN也能 Inductive Learning(比如Graph的分类),与常见的 Transductive Learning 不同,归纳式的图学习会明确地把图数据划分成训练集和验证集,通过封闭式地学习训练集,再处理验证集;比如 PPI 数据集(与蛋白质结构相关),共24个Graph,一般将前22个Graph作为训练集,剩下的2张Graph用于验证;
Inductive Learning:从特殊到一般
Transductive Learning:从特殊到特殊
半监督Semi-supervised Learing主要考虑如何利用少量的标注样本和大量的未标注样本进行训练和分类。因此,半监督学习的训练集中一部分样本有标注,一部分样本是无标注的,半监督学习的目标是将模型泛化到测试集上(测试集样本同样没有标注)。
Transductive Learing假设未标记的数据就是最终要用来测试的数据,学习的目的就是在这些未标记数据上取得最佳泛化能力(从这个角度看,直推式学习没有训练集和测试集的区分)。相对应的,半监督学习在训练时并不知道最终的测试样本的任何信息。
我们可以把直推式学习看成是一种特殊的半监督学习。
GraphSAGE
图采样聚合网络又称 GraphSAGE(Graph SAmple and aggreGatE),GraphSAGE是一种迭代算法,用于学习某个图中每个节点的嵌入(embedding),嵌入反映了节点的特征所发生的变换;GraphSAGE在论文"Inductive Representation Learning on Large Graphs
"中首次提出 Inductive Learning 与 Transductive Learning 在GNN上的应用;
GraphSAGE的新奇之处在于它是第一个以无监督的方式创建归纳节点嵌入(inductive node embeddings)的工作;
GraphSAGE的目标是学习每个节点基于其邻近节点的某种组合的表示。GCN研究信息的聚合,GraphSAGE则是研究更好地完成信息聚合;
- N ( v ) N(v) N(v):任意节点 v v v的邻居节点集合;
- x v x_{v} xv:任意节点 v v v的特征;
- h v 0 h_{v}^{0} hv0:任意节点 v v v的初始节点嵌入(node embedding), h v 0 = x v h_{v}^{0}=x_{v} hv0=xv;
- h v k h_{v}^{k} hvk:迭代 k k k次后,节点 v v v的嵌入表达;
- z v z_{v} zv:通过一轮GraphSAGE算法后,节点 v v v的最终嵌入表达;
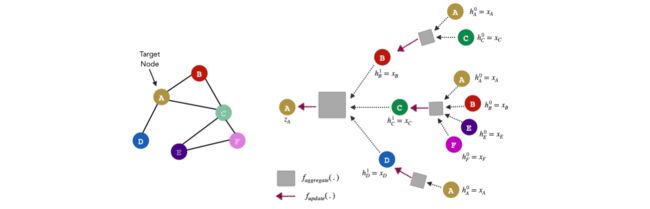
由于每个节点都可以由其邻居定义,因此节点 A 的嵌入可以用其邻居节点嵌入向量的某种组合来表示;通过一轮GraphSAGE算法,我们将得到节点 A 特征的一个新表达;过程如下:

从上图看出,信息聚合分两步,先通过 f a g g r e g a t e f_{aggregate} faggregate聚合邻居的信息,再通过 f u p d a t e f_{update} fupdate融合节点自身的信息并更新节点的嵌入表达:
- Aggregate,聚合邻居信息: a v = f a g g r e g a t e ( { h u ∣ u ∈ N ( v ) } ) a_{v}=f_{aggregate}(\left\{h_{u}|u\in N(v)\right\}) av=faggregate({hu∣u∈N(v)})
- Update,更新节点的嵌入表达: h v k = f u p d a t e ( a v , h v k − 1 ) h_{v}^{k}=f_{update}(a_{v},h_{v}^{k-1}) hvk=fupdate(av,hvk−1)
参数 k k k 告诉算法使用多少层邻域或多少跳来计算节点 v v v 的表示,一般迭代跳数为2,即信息聚合范围到二阶邻居:
一个节点可以扩展出过多的邻居节点,为了降低计算量,GraphSAGE会在对象节点的邻居集合中采样,原文中的例子为:
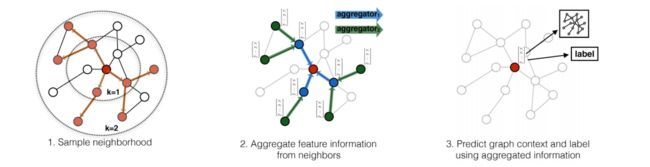
对邻居采样,一阶邻居采样多一点,对于每个一阶邻居的邻居(二阶邻居)采样少一点,这是因为一阶邻居与对象节点的关系更大;从采样后的节点中聚合信息并更新,得到对象节点的高层信息(获得嵌入表达);
算法流程
输入为:Graph G ( V , E ) G(V,E) G(V,E),节点的特征{ x v ∣ v ∈ V x_{v}|v\in V xv∣v∈V},迭代次数或者跳数 K K K,权值矩阵{ W k ∣ k ∈ { 1 , . . . , K } W^{k}|k\in \left\{1,...,K\right\} Wk∣k∈{1,...,K}},非线性函数 σ \sigma σ,可微的聚合函数{ A G G R E G A T E k ∣ k ∈ { 1 , . . . , K } AGGREGATE_{k}|k\in \left\{1,...,K\right\} AGGREGATEk∣k∈{1,...,K}},返回邻居集合的函数 ℘ \wp ℘;
输出为任意节点 v v v的嵌入表达 z v z_{v} zv;
GraphSAGE的算法描述如下:
- step1.初始化节点嵌入 h v 0 = x v h_{v}^{0}=x_{v} hv0=xv;
- step2.对于迭代的第 k k k步( k ∈ { 1 , . . . , K } k\in \left\{1,...,K\right\} k∈{1,...,K}),对于每个节点都进行操作,比如对于节点 v v v,聚合其邻居的信息,并更新:
h ℘ ( v ) k = A G G R E G A T E k ( { h u k − 1 ∣ u ∈ ℘ ( v ) } ) h_{\wp(v)}^{k}=AGGREGATE_{k}(\left\{h_{u}^{k-1}|u\in \wp(v)\right\}) h℘(v)k=AGGREGATEk({huk−1∣u∈℘(v)})
h v k = σ ( W k ⋅ C O N C A T ( h v k − 1 , h ℘ ( v ) k ) ) h_{v}^{k}=\sigma (W^{k}\cdot CONCAT(h_{v}^{k-1},h_{\wp(v)}^{k})) hvk=σ(Wk⋅CONCAT(hvk−1,h℘(v)k)) - step3.在迭代的第 k k k步,已处理完所有节点后,归一化节点嵌入:
h v k = h v k ∣ ∣ h v k ∣ ∣ 2 , v ∈ V h_{v}^{k}=\frac{h_{v}^{k}}{||h_{v}^{k}||_{2}},v\in V hvk=∣∣hvk∣∣2hvk,v∈V
如果还未迭代到第 K K K步,则更新 k = k + 1 k=k+1 k=k+1,回到step2; - step4.输出 z v = h v K , v ∈ V z_{v}=h_{v}^{K},v\in V zv=hvK,v∈V
注意,邻居函数 ℘ \wp ℘与迭代次数有关,如果 k = 1 k=1 k=1,则任意节点 v v v的邻居集合 ℘ ( v ) \wp(v) ℘(v)为其一阶邻居,如果 k = 2 k=2 k=2,则 ℘ ( v ) \wp(v) ℘(v)为该节点的邻居的一阶邻居(节点 v v v本身也算);
一般迭代次数为 K = 2 K=2 K=2;
GraphSAGE与InductiveLearning的关系
通过以上内容,容易发现GraphSAGE与GCN有一个很大的区别,GCN是Transductive learning的方式,需要让所有节点都参与训练才能得到 node embedding,不便于得到新增节点的embedding,缺少通用性;
GraphSAGE的目标不在于分类节点或预测边,其目的是寻求一种新的节点嵌入表达方式,即通过从一个节点的局部邻居采样再聚合特征;对于新的节点信息,TransdutiveLearning不能自然地泛化到未见过的节点,而GraphSAGE可以动态地聚合出新节点的embeddinng信息;
在大型图中,节点的低维向量embedding被证明了作为各种各样的预测和图分析任务的特征输入是非常有用的。embedding的基本思想是使用降维技术从高维信息中提炼节点的邻居信息,存到低维向量中。这些embedding会作为后续的机器学习模型的输入,解决节点分类、聚类、链接预测等问题;
GCN等transductive的方法,学到的是每个节点上唯一确定的embedding; 而GraphSAGE方法学到的embedding,是根据节点邻居关系的变化而变化的,比如:即使是旧的节点,如果建立了一些新的连接,那么其对应的embedding也会变化,而且也是可以方便地计算得出的;
损失函数
GraphSAGE的损失函数较为特殊,先将图经过GraphSAGE映射到嵌入空间:

节点在嵌入空间中的距离与节点之间边的连接关系相关;其损失函数的思想为:如果节点 u u u和 v v v是邻居,则希望两者的嵌入空间距离变小,如果不是邻居,则希望距离变大,所以对于训练数据中的一个节点 u u u的损失函数为:
l ( z u ) = − ( l o g ( σ ( z u T z v ) ) + Q ⋅ E v n ∼ P n ( v ) [ l o g ( σ ( − z u T z v n ) ) ] ) l(z_{u})=-(log(\sigma(z_{u}^{T}z_{v}))+Q\cdot E_{v_{n}\sim P_{n}(v)}[log(\sigma(-z_{u}^{T}z_{v_{n}}))]) l(zu)=−(log(σ(zuTzv))+Q⋅Evn∼Pn(v)[log(σ(−zuTzvn))])
其中, z v z_{v} zv是一个与节点 u u u相连的随机节点的embedding, Q Q Q定义了负样本数量, P n P_{n} Pn是负样本的分布;
GraphSAGE是一种无监督学习模型
注意力机制简介
注意力:聚焦于输入的特定部分;注意力已被广泛应用于深度学习中,用于语音识别、机器翻译和计算机视觉;比如视觉下的注意力 Visual Attention:

可视化注意力分布后可以发现,注意力更多地集中在兔子这个对象上,这与人类的视觉习惯是符合的,人眼在观看图像时,不会把精力放到所有对象上,人总会更多地注意当前图像内的个别对象;
视觉注意:关注视觉输入的特定部分,以计算足够的响应;这一原理对神经网络计算有很大的影响,因为我们需要选择最相关的部分信息,而不是使用所有可用的信息,因为其中很大一部分与神经网络的响应无关;
注意力无处不在(“Attention is all you need”),注意力最早出现在自然语言处理方向,即文本下的注意力 Text Attention:

可以看出,文本内不同的单词之间存在不同程度的关联,比如 colonize(殖民)与 planet(星球)存在关系;粗略地认为,这属于自注意力(Self-Attention,自注意力回顾 pytorch笔记本第十四课-Transformer);
注意力机制的详细内容回顾 pytorch笔记本第十四课-Transformer
注意力机制分类各异,但在计算机视觉,语音识别和自然语言处理等深度学习任务中,常见到一个普遍的工程结构:Attention Model,注意力模型总会按照两个步骤计算:
- 1.在输入信息上计算注意力分布;
- 2.根据注意力分布计算输入信息的加权平均;
Attention Model 的结构如下:

以柔性注意力 Soft-Attention 为例,假设对于一个文本,当前有 n n n个输入的词信息 ( y 1 , y 2 , . . . , y n ) (y_{1},y_{2},...,y_{n}) (y1,y2,...,yn),另外有来自上文的信息 c c c,通过Attention Model得到需要的输出信息 z z z;进一步分析Attention Model:

首先,输入的 c c c是上文信息(一个向量), y i y_{i} yi是当前输入的词信息(一个向量),计算 m i m_{i} mi:
m i = t a n h ( W c m c + W y m y i ) m_{i}=tanh(W_{cm}c+W_{ym}y_{i}) mi=tanh(Wcmc+Wymyi)
m i m_{i} mi意味着计算了 y i y_{i} yi和 c c c的"聚合";对于聚合结果,使用softmax得到注意力的分布 s i s_{i} si:
s 1 , s 2 , . . . , s n = s o f t m a x ( m 1 , m 2 , . . . , m n ) s_{1},s_{2},...,s_{n}=softmax(m_{1},m_{2},...,m_{n}) s1,s2,...,sn=softmax(m1,m2,...,mn)
按照注意力的分布计算加权平均:
z = ∑ i = 1 n s i y i z=\sum_{i=1}^{n}s_{i}y_{i} z=i=1∑nsiyi
输出 z z z为所有 y i y_{i} yi的加权平均值,其中权重表示根据上文信息 c c c对每个输入词 y i y_{i} yi的相关性;
Soft-Attention中的一个特点是计算所有的输入信息,现在补充一个与之相反的 Hard-Attention;Hard-Attention的特点是随机处理:系统不使用所有的状态作为输入,而是以一定概率采样一个状态 y i y_{i} yi,可以先采样,再计算注意力分布并加权平均,也可以先统一计算注意力分布,再采样后加权平均:

直观看Soft-Attention与Hard-Attention,Soft-Attention由于会考虑所有输入信息,如果处理的是视觉对象,则会发现模型在某些边角位置上也投入注意力,而Hard-Attention不容易出现这种情况
图注意力网络
GAT
图注意力网络(Graph Attention Network)是GNN与Attention的结合,图注意力网络简称GAT,来源于论文"GRAPH ATTENTION NETWORKS";比如:

对于图中的部分数据 V i V_{i} Vi,在围绕中心节点 i i i聚合信息时,从中心节点到周围邻居,各节点对应的信息权重逐渐降低,通过加权平均后得到最终的聚合信息,这就是GAT的思想;
在实际应用中,GAT层只关注基于目标节点的一阶邻居信息:

和之前的GraphSAGE的信息聚合方式比较,除了取消采样和聚合范围(邻居范围)缩小外,GAT在聚合信息前增加了权重(注意力);通过引入注意力分布,可以得到各个邻居对目标节点的重要程度;
注意:邻接矩阵只能反映图的结构,只能反映节点之间是否连接,不能反映众多邻居节点在目标节点之间各异的重要程度
GAT采用了多头注意力机制(Multi-Head Attention,回顾 pytorch笔记本第十四课-Transformer),多头注意力相当于给出了注意力层的多个"表示空间",即融合了不同角度的注意力信息,GAT的算法流程为:
- step1.对节点的特征进行线性变换,对于节点 i i i,其特征为 h i h_{i} hi,通过可学习的矩阵 W W W进行变换: W h i Wh_{i} Whi;
- step2.计算注意力分布,比如两个相邻节点 i i i和 j j j,注意力系数 a i j a_{ij} aij反映了节点 j j j的信息对节点 i i i的重要程度( N ( i ) N(i) N(i)为节点 i i i的一阶邻居集合):
a i j = e x p ( [ W h j ] T [ W h i ] ) ∑ k ∈ N ( i ) e x p ( [ W h k ] T [ W h i ] ) a_{ij}=\frac{exp([Wh_{j}]^{T}[Wh_{i}])}{\sum_{k\in N(i)}exp([Wh_{k}]^{T}[Wh_{i}])} aij=∑k∈N(i)exp([Whk]T[Whi])exp([Whj]T[Whi]) - step3.加权平均得到输出的特征表达:
h ^ i = σ ( ∑ k ∈ N ( i ) a i k [ W h k ] ) \widehat{h}_{i}=\sigma(\sum_{k\in N(i)}a_{ik}[Wh_{k}]) h i=σ(k∈N(i)∑aik[Whk]) - step4.拼接各个自注意力输出的特征表达得到多头注意力的特征表达;不同的自注意力对应不同的可学习矩阵 W W W,假设共 n n n个注意力,则拼接为:
h ^ i = C O N C A T ( σ ( ∑ k ∈ N ( i ) a i k 1 [ W 1 h k ] ) , σ ( ∑ k ∈ N ( i ) a i k 2 [ W 2 h k ] ) , . . . , σ ( ∑ k ∈ N ( i ) a i k n [ W n h k ] ) ) \widehat{h}_{i}=CONCAT(\sigma(\sum_{k\in N(i)}a_{ik}^{1}[W^{1}h_{k}]),\sigma(\sum_{k\in N(i)}a_{ik}^{2}[W^{2}h_{k}]),...,\sigma(\sum_{k\in N(i)}a_{ik}^{n}[W^{n}h_{k}])) h i=CONCAT(σ(k∈N(i)∑aik1[W1hk]),σ(k∈N(i)∑aik2[W2hk]),...,σ(k∈N(i)∑aikn[Wnhk]))
GaAN
在GAT中,多头注意力的融合总是平均地加入各个注意力信息,为了在多头注意力的基础上再增加注意力,提出门控图注意力网络,简称GaAN(Gated Graph Attention Network),来源于论文"GaAN: Gated Attention Networks forLearning on Large and Spatiotemporal Graphs",GaAN的目标是将注意力设置得更透彻
