用于图卷积神经网络的可解释性方法CVPR2019

在此之前，为了正确理解下面的各种方法，我们需要明白一个问题，目前的可解释性方法，它们最多都只能获得关于最终预测结果在不同层级上的特征感知，而不能获得某个高层语义特征下的低层特征的感知关系。并且，下面这些工作依然没有解决这个问题。

激励反向传播Excitation Backprop(ECCV2016)

现代的CNN模型总是由基本的神经元$a_i$组成，其响应为$a_i=\varphi ({\sum }_j{w}_{ji}{a}_j+b_j)$，其中$w_{ji}$是权重，$a_j$是输入。我们把这种类型的神经元叫激活神经元。对于激活神经元，我们有下面假设：

• A1：激活神经元的响应为非负性；
• A2：激活神经元被调整以检测某些视觉特征。其响应与其检测的置信度呈正相关。

A1适用于大多数现代CNN模型，因为它们采用ReLU作为激活函数。A2已经被最近的许多工作验证。据观察，较低层次的神经元可以检测边缘和颜色等简单特征，而较高层次的神经元可以检测物体和body部位等语义特征。

在激活神经元之间，我们定义一种连接，如果其权重$w_{ji}$为非负，则为兴奋性（excitatory），否则为抑制性（inhibitory）。我们的激励反向传播通过激活神经元之间的兴奋性连接传递着自顶向下（top-down）的信号。形式上，用$C_i$表示$a_i$的子节点集（节点的graph按照top-down顺序描述，$C_i$的元素是有兴奋性连接到$a_i$的一阶子节点）。对于每个$a_j\in C_i$，条件获胜概率$P(a_j|a_i)$为：

其中，$Z_i=1/{\sum }_{j:w_{ji}\ge 0}{a}_j{w}_{ji}$是归一化因子，比如${\sum }_{a_j\in C_i}P(a_j|a_i)=1$。特别的，如果${\sum }_{j:w_{ji}\ge 0}{a}_j{w}_{ji}=0$，我们定义$Z_i=0$，注意到，$P(a_j|a_i)$因为A1而有效，因为$a_j$总是非负的。

上面式子假设如果$a_i$是获胜神经元，下一个获胜神经元将会在它的子节点集$C_i$中采样（基于连接权重$w_{ji}$和输入神经元的响应$a_j$）。权重$w_{ji}$捕捉了top-down的特征期望，$a_j$代表bottom-up的特征强度，正如A2所述。由于A1，具有负连接权重的$a_i$的子神经元总是对$a_i$有抑制作用，因此被排除在竞争之外。

---

换言之，$P(a_j|a_i)$表示：当$a_i$是获胜神经元时，对于与其有兴奋性连接的一阶神经元，各个神经元$a_j$对$a_i$产生影响的强度大小。

---

用上面那个公式逐层递归传播自上而下的信号，我们可以从任何中间卷积层计算注意力图。对于我们的方法，我们只需将跨通道的feature maps求和生成一个边缘获胜概率图（MWP，marginal winning probability，边缘概率分布）作为我们的注意力图，即2D概率直方图。下图显示了使用预训练的VGG16模型生成的一些MWP图示例。更高层的神经元有更大的感受野和步幅。因此，它们可以捕获更大的区域，但空间精度较低。较低层次的神经元倾向于在较小的尺度上更精确地定位特征。

• 边缘获胜概率（MWP）图，通过在ImageNet上训练的公共VGG16模型的不同层的激励Backprop计算得出。更高层的神经元有更大的感受野和步幅。因此，它们可以捕获更大的区域，但空间精度较低。较低层次的神经元倾向于在较小的尺度上更精确地定位特征。

训练用的反向传播是在传播误差以更新梯度，激励反向传播则是传递激励信号。反向传播目的是为参数传播得到梯度，并进行element-wise的相减的更新，激励反向传播则是传播得到特征图的逐像素的概率程度，我们需要进行element-wise相乘的更新。最后得到的MWP是关于最终预测结果在不同层级上的特征感知。

摘要

随着图卷积神经网络（GCNNs）的广泛使用，对其可解释性的需求也随之产生。本文介绍了GCNNs的可解释性方法。我们为卷积神经网络开发了三种重要的可解释性方法的图类似物：基于梯度的对比显著性图（CG，contrastive gradient-based）、类激活映射（CAM，Class Activation Mapping）和激励反向传播（EB，Excitation Backpropagation）及其变体、梯度加权CAM（Grad-CAM，gradient-weighted CAM）和对比EB（c-EB，contrastive EB）。我们在两个应用领域：视觉场景图和分子图的分类问题上证明了这些方法可行。为了比较这些方法，我们确定了三个理想的可解释属性：（1）它们对分类的重要性，通过遮挡的影响来衡量，（2）它们对不同类别的对比度，以及（3）它们在图上的稀疏性。我们将相应的量化指标称为保真度（fidelity）、对比度（contrastivity）和稀疏度（sparsity），并对每种方法进行评估。最后，我们分析了从解释结果中获得的显著性子图，并报告了一些频繁出现的模式。

1.Introduction

计算机视觉领域最近的成功主要归功于深度卷积神经网络（CNN）的出现。这导致了在各种计算机视觉任务上的最新表现，包括目标识别、目标检测和语义分割。CNN的端到端学习特性使其成为从大量视觉数据学习的强大工具。同时，这种端到端的学习策略阻碍了CNN决策的可解释性。最近，有越来越多的研究CNN内部工作机制的著作。

然而，深层CNN是为欧几里德空间中的网格结构数据（如图像）而设计的，因为卷积是在欧几里德空间上定义的一种操作，用于有序元素的输入。尽管如此，在许多应用中，我们需要处理在不同结构上定义的数据，例如图graph和流形manifold，这种情况下CNN不能直接使用。这种非欧几里德空间出现在各种应用中，包括场景图分析、3D形状分析、社交网络和化学分子结构。几何深度学习是最近兴起的一个领域，旨在克服CNN的局限性并拓宽其应用范围。特别是，通过将卷积运算扩展到图和一般非欧几里德空间，可以将CNN推广到适用于图结构数据。将CNN扩展到非欧几里德空间导致了图卷积神经网络（GCNN）的出现。

除了模型的优异性能之外，我们还需要一些技术来解释为什么模型会预测它所预测的内容。这种解释有助于识别与特定任务中模型决策相关的部分输入数据。受CNN可解释性工作的启发，我们介绍了GCNNs决策的可解释性方法。可解释性对图尤其有用，甚至比图像更有用，因为非专家人员无法直观地确定图中的相关上下文，例如，识别有助于分类分子特定属性的原子组（分子图上的子结构）。

我们采用了最初为CNN设计的三种常见解释方法，并将其扩展到GCNNs。这三种方法是基于梯度的显著性图、类激活映射（CAM）和激励反向传播（EB）。此外，我们采用了两种变体：梯度加权CAM（Grad CAM）和对比EB。我们将改进方法用于两种不同的场景：视觉场景图（visual scene graphs）和分子图（molecular graphs）。对于GCNNs，我们使用Kipf等人提出的公式。我们在这项工作中的具体贡献有以下三点：

• 将CNN的可解释方法迁移到GCNN；
• 两个图分类问题的可解释性技术演示：视觉场景图和分子图；
• 使用保真度、对比度和稀疏度指标描述每种方法。

本文的其余部分结构如下。在第2节中，我们讨论了可解释性和GCNNs的相关工作。在第3节中，我们回顾了GCNNs的数学定义和CNN上的可解释方法，然后定义了GCNNs上的类似可解释方法。在第4节中，我们详细介绍了我们在视觉场景图和分子上的实验，并给出了示例结果。此外，我们还从三个指标（保真度、对比度和稀疏度）对这四种方法的性能进行了定量评估，每个指标都旨在捕捉可解释的某些理想特性。我们使用这些指标来评估每种方法的优点。最后，在实验部分，我们分析了Grad CAM识别的显著子结构，并报告了每个数据集的最佳结果。

2.Related Work

2.1.Interpretability

一般深层神经网络的一个长期局限性是难以解释分类结果。最近，针对深层网络，特别是CNN设计了可解释性方法。这些方法使人们能够探测CNN并识别输入数据的重要子结构，以便就任务做出决策，这可以用作解释工具或发现数据中未知底层子结构的工具。例如，在医学成像领域，除了对具有恶性病变的图像进行分类外，还可以对其进行定位，因为CNN可以为输入图像的分类提供推理。

在输入数据上生成灵敏度图（sensitivity map）以发现底层子结构重要性的最直接方法是，通过考虑输出相对于网络输入的梯度来计算梯度图。然而，梯度图通常包含过度的噪声。更先进的技术包括类激活映射（CAM，Class Activation Mapping）、梯度加权类激活映射（Grad-CAM）和激励反向传播（EB）通过考虑上下文的一些概念来改进梯度图。这些技术已被证明对CNN有效，并且可以识别图像中高度抽象的概念。

2.2.GCNNs

GCNNs的数学基础深深植根于图处理和图论领域，在图论中，傅里叶变换和卷积等信号运算被扩展到图上的信号。基于图论的GCNN可以定义类似于CNN的参数化滤波器。然而，它们的计算成本往往很高，因此速度很慢。为了克服谱GCNN的计算瓶颈，许多作者提出在谱域中近似平滑滤波器，例如使用切比雪夫多项式或图卷积的一阶近似。在这项工作中，我们使用Kipf和Welling定义的GCNN公式，因为它的训练时间更快，预测精度更高。

GCNN最近得到了广泛应用。Monti等人使用GCNNs进行超像素分类，以及对引文网络中的研究论文进行分类。Defferard等人使用Ngrams上的GCNNs进行文本分类。GCNN也可以用于形状分割，用于基于骨架的动作识别。最近，Johnson等人使用GCNNs分析场景图，并应用场景图生成图像。在化学中，GCNN被用来预测有机分子的各种化学性质。GCNN在一些化学预测任务上提供了最先进的性能，包括毒性预测、溶解度预测和能量预测。本文主要研究GCNNs的可解释性方法及其在场景图分类和分子分类中的应用。

3.Method

我们比较和对比了常用的可解释性方法在图卷积神经网络（GCNN）中的应用。此外，我们还探讨了对这些方法进行一些增强的好处。

3.1.Explainability for CNNs

三种主要的解释方法是对比梯度法（contrastive gradients）、类激活映射法（Class Activation Mapping）和激励反向传播法（Excitation Backpropagation）。

基于对比梯度的显著性图（Contrastive gradient-based saliency maps）可能是最直接最成熟的方法。在这种方法中，只需要区分模型输出与模型输入，因此，可以创建一个heat map，其中，输出相对输入变量上的梯度表示该输入相对于输出的重要性。因此，舍弃梯度中的负值，仅保留对解决方案有积极贡献的输入部分：$$L_{Gradient}^c=||ReLU(\frac{\partial y^c}{\partial x})||$$其中，$y^c$是类别$c$在softmax前的得分，$x$是输入。虽然很容易计算和解释，但显著图（saliency maps）的性能通常比新技术（如CAM、Grad CAM和EB）差，因为最近有研究表明显著图倾向于表示噪声而不是真实信号。

类激活映射（Class Activation Mapping）通过在最后一个卷积层识别重要的类特定特征，从而改进了卷积神经网络（包括GCNN）的显著性图。众所周知，这些特征往往在语义上更有意义。CAM的缺点是，它要求紧靠softmax分类器（输出层）之前的层是卷积层，然后是全局平均pooling（GAP）层。这就排除了使用更复杂、异构的网络，例如那些在softmax层之前包含几个全连接的层的网络。

为了计算CAM，令$F_k\in R^{u\times v}$是softmax之前那个卷积层输出的第$k$个特征图，记$F_k$的全局平均pooling为：$$e_k=\frac{1}{uv}\sum _i\sum _j{F}_{k,i,j}$$然后，得到类别的得分$y_c$：$$y_c=\sum _k{w}_k^c{e}_k$$权重$w_k^c$编码了特征$k$对于预测类别$c$的重要性。通过将每个特征图upsample到输入图像的大小，像素空间中的 class-specific heat-map 为：$$L_{CAM}^c[i,j]=ReLU(\sum _k{w}_k^c{F}_{k,i,j})$$Grad-CAM方法通过放宽倒数第二层必须是卷积的架构限制，对CAM进行了改进。这是通过使用基于反向传播梯度的特征图权重${\alpha }_k^c$来实现的。具体而言，Grad-CAM定义权重为：$${\alpha }_k^c=\frac{1}{uv}\sum _i\sum _j\frac{\partial y^c}{\partial F_{k,i,j}}$$对于Grad-CAM，像素空间中的heat-map计算如下：$$L_{GradCAM}^c[i,j]=ReLU(\sum _k{\alpha }_k^c{F}_{k,i,j})$$其中，ReLU函数确保只有对类别预测有积极影响的特征是非零的。

激励反向传播（Excitation Backpropagation）令$a_i^l$是layer $l$ 的第$i$个神经元，$a_j^{l-1}$ 是layer ($l-1$)的神经元。定义神经元$a_j^{l-1}$对于神经元$a_i^l$的激活$y_i^l\in R$的相对影响（relative influence），其中，$y_i^l=\sigma ({\sum }_{ji}{W}_{ji}^{l-1}{y}_j^{l-1})$，$W^{l-1}$是层$l-1$和层$l$之间的权重。概率分布可以表示为：$$P(a_j^{l-1})=\sum _{i}P(a_j^{l-1}|a_i^l)P(a_i^l)$$其中，条件分布为：

其中：$$Z_i^{l-1}=(\sum _j{y}_j^{l-1}{W}_{ji}^{l-1}{)}^{-1}$$是归一化因子，比如${\sum }_{j}P(a_j^{l-1}|a_i^l)=1$。对于给定输入（比如图像），EB通过在输出层$P(a_i^L=c)=1$递归调用上面的概率分布等式，并在像素空间生成类别$c$对应的热图。

可以看出，这些解释方法都有局限性：它们最多都只能获得关于最终预测结果在不同层级上的特征感知，而不能获得某个高层语义特征下的低层特征的感知关系。

这些解释性方法最初是为CNN设计的，CNN是为均匀方形网格上的信号定义的。这里，我们对非欧几里德结构（如图）支持的信号感兴趣。下面，我们首先简要讨论GCNNs，然后描述这些可解释性方法对GCNNs的扩展。直觉上，我们注意到图像可以被概念化为点阵图形，像素值作为节点特征。从这个意义上讲，GCNN是广义的CNN。

3.2.Graph Convolutional Neural Networks

设图具有$N$个节点，节点属性为$X\in R^{N\times d_{in}}$，邻接矩阵为$A\in R^{N\times N}$（带权重或者二值的都可以）。另外，度矩阵为：$D_{ii}={\sum }_j{A}_{ij}$。继Kipf和Welling的工作之后，我们将图卷积层定义为：$$F^l(X,A)=\sigma ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{F}^{l-1}(X,A)W^l)=\sigma (V{F}^{l-1}(X,A)W^l)$$其中，$F^l$是第$l$层的卷积，$F^0=X$，$\tilde{A}=A+I_N$是引入节点自连信息后的邻接矩阵。${\tilde{D}}_{ii}={\sum }_j{\tilde{A}}_{ij}$，$W^l\in R^{d_l\times d_{l+1}}$为可学习参数。$\sigma$是element-wise非线性函数。图1显示了本工作中使用的GCNN架构。

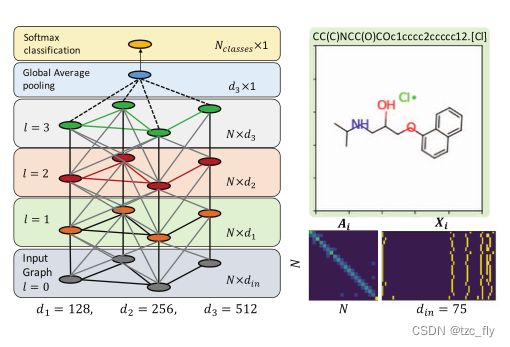
• 图1：我们的GCNN+全局平均pooling架构，以及BBBP数据集中样本分子的输入特征和邻接矩阵的可视化。

对于分子分类，每个分子都可以表示为一个图$G_i=(X_i,A_i)$，其中，节点特征$X_i$总结了分子中原子的局部化学环境，包括原子类型atom-types、杂化类型hybridization types和价结构valence structures，邻接矩阵编码原子的键并显示整个分子的连接性（见图1）。对于给定的有标签数据集$D=(G_i,y_i{)}_{i=1}^M$，标签$y_i$表示某种化学性质，比如血脑屏障渗透性（blood-brain-barrier penetrability）或毒性（toxicity），任务是学习一种分类器，将每个分子映射到相应的标签上。

鉴于我们的任务是对具有潜在不同节点数的单个图（即分子）进行分类，我们使用几层图卷积层，然后在图节点（例如原子）上使用全局平均pooling（GAP）层。在这种情况下，所有图都将用固定大小的向量表示。最后，将特征传给分类器。为了实现CAM的适用性，我们仅在GAP层后使用softmax分类器。

3.3.Explainability for Graph Convolutional Neural Networks

在这一小节中，我们描述了CNN解释方法对GCNNs的扩展。将$l$层的第$k$个图卷积特征图定义为：$$F_k^l(X,A)=\sigma (V{F}^{l-1}(X,A)W_k^l)$$其中，$W_k^l$表示矩阵$W^l$的第$k$列，在这种表示法中，对于节点$n$，第$l$层的第$k$个特征用$F_{k,n}^l\in R$表示。然后，最后卷积层$L$之后的GAP特征，计算为：$$e_k=\frac{1}{N}\sum _{n=1}^N{F}_{k,n}^L(X,A)\in R$$该图属于类别$c$得分为$y^c={\sum }_k{w}_k^c{e}_k$，我们将可解释性方法扩展到GCNNs，如下所示：

Gradient-based 对于节点$n$的热力图为：$$L_{Gradient}^c[n]=||ReLU(\frac{\partial y^c}{\partial X_n})||$$
CAM 热力图计算为：$$L_{CAM}^c[n]=ReLU(\sum _k{w}_k^c{F}_{k,n}^L(X,A))$$
Grad-CAM在层$l$处$c$类和特征$k$的类特定权重计算如下：$${\alpha }_k^{l,c}=\frac{1}{N}\sum _{n=1}^N\frac{\partial y^c}{\partial F_{k,n}^l}$$并且第$l$层的热力图计算为：$$L_{GradCAM}^c[l,n]=ReLU(\sum _k{\alpha }_k^{l,c}{F}_{k,n}^l(X,A))$$Grad-CAM使我们能够生成位于网络不同层的热力图。此外，对于图1所示的模型，最后一个卷积层的Grad-CAM热图和CAM热图是等效的。

Excitation Backpropagation 我们的模型的激励反向传播热图是通过反向传播softmax分类器、GAP层和几个图卷积层来计算的。反向传播softmax分类器和GAP层的方程如下：

其中，对于感兴趣类别，$p(c)=1$，否则为0。然而，图卷积层的反向传播更加复杂。为了符号的简化，我们将图卷积算子分解为：

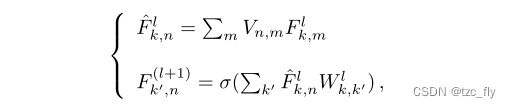
其中，第一个方程是原子的局部平均值。第二个方程是应用于每个原子的固定感知机（类似于CNN中的逐个卷积）。这两个函数的反向传播定义为：

我们通过反向传播网，得到输入级别上的热图：$$L_{EB}^c[n]=\frac{1}{d_{in}}\sum _{k=1}^{d_{in}}p(F_{k,n}^0)$$我们将这种图数据上的EB称为c-EB。

4.Experiments

4.1.视觉场景解释

我们的目标是训练用于场景图分类的GCNN，并在这些GCNN上使用我们提出的可解释性方法。场景图是一种图结构数据，其中节点是场景中的对象，边是对象之间的关系。我们从Visual Genome dataset获得了第一次实验的数据。Visual Genome dataset由图像和场景图对组成（images and scene graph pairs）。对象和关系有多种类型，对象由bounding box关联到图像中的区域。

我们从Visual Genome构建了两个场景图上的二元分类任务：国家与城市（country vs. urban），以及室内与室外（indoor vs outdoor）。我们用一组关键字对这些单词进行建模，这些关键字用于查询Visual Genome数据，以匹配图像的任何属性。类的图像集为每个关键字返回的图像集的并集。此外，删除了类对之间的任何交集。用于定义每个类的关键字如下：

• “country”: country, countryside, farm, rural, cow,
  crops, sheep
• “urban”: urban, city, downtown
• “indoor”: indoor, room, office, bedroom, bathroom
• “outdoor”: outdoor, nature, outside

为简单起见，在不损失泛化性的情况下，我们将所有关系折叠为单一类型，表示两个对象之间存在通用关系。

场景图中有一个与每个对象（即节点）关联的边界框。我们使用预训练的InceptionV3网络，为场景图所有节点的边界框提取底层图像的深层特征。最后一个pooling层被用作视觉特征，其中每个crop都被零填充到一个固定的大小。从每个边界框提取的特征的大小为$d=2048$。因此，我们导出的场景图由关系数据和视觉数据组成。最后的任务是将场景图分为城市与乡村、室内与室外两类。

4.2.分子图解释

我们研究第二个应用领域：识别有机分子上的官能团以获得生物分子特性。我们评估了3个两分类分子数据集，BBBP、BACE和TOX21中的任务NR-ER。每个数据集包含由实验确定的有机小分子的二元分类。BBBP数据集包含了一种分子是否渗透人类血脑屏障的测量结果，对药物设计有重要意义。BACE数据集包含一个分子是否抑制人类β-分泌酶的测量结果。TOX21数据集包含多个毒性目标的分子测量。我们从这些数据中选择了NR-ER任务，该任务与雌激素受体的激活有关。

4.3.三个量化指标

我们报告了三个量化指标，它们衡量了可解释的保真度、对比度和稀疏性（fidelity，contrastivity 和 sparsity）。

计算保真度是为了捕捉这样一种直觉，即通过遮挡解释得到的显著性特征会降低分类精度。更准确地说，我们将保真度定义为通过遮挡所有显著性值大于0.01（在0到1的范围内）的节点而获得的Acc差异。然后，我们平均每种方法在不同class的保真度得分。

对比度旨在捕捉这样一种直觉，即解释方法所强调的特定于类别的特征应该在不同的类别之间有所不同。更准确地说，我们将对比度定义为正类和负类的二值化热图（注意是graph结构的热图）$m_0,m_1$之间的汉明距离$d_H$（回顾其他算法-LSH局部敏感度哈希）的归一化：$$\frac{d_H(m_0,m_1)}{m_0\cup m_1}$$

稀疏性是用来衡量解释的局部化程度。稀疏解释对于研究大型图特别有用，因为手动检查所有节点是不可行的。更准确地说，我们将此度量定义为：$$1-\frac{m_0}{|V|}$$其中，$|V|$为节点数量。

4.4.结果

• 图2：每个Visual Genome dataset的选定解释结果。所有示例的边界框都显示在输入列中。边界框根据其显著性值（红色：低，绿色：高）着色。每种方法都显示了前5个对象，以减少混乱。“class 0”是指国家或室外。“class 1”指城市或室内。对比度可以通过比较每个方法的类之间的区域来看到，例如，gradient-based方法倾向于突出显示两个类的相同特征，而CAM和GradCAM倾向于突出显示不同的对象。

• 图3：每个分子数据集的选定解释结果。每个样本都是真阳性。深蓝色表示与给定类的相关性更高。从稀疏性可以看出，例如在EB中，注意到EB比其他方法突出显示的原子更少。

个人总结

• 目前的可解释性方法，它们最多都只能获得关于最终预测结果在不同层级上的特征感知，而不能获得某个高层语义特征下的低层特征的感知关系。并且，上面这些工作依然没有解决这个问题；
• 可解释的三个指标：fidelity，contrastivity 和 sparsity；
• 激励反向传播和Grad-CAM或许可以作为一种后验修正，用于做视觉表现提升与泛化的工作。