动态面板案例分析
动态面板模型分析
如果在面板模型中,解释变量包括被解释变量的滞后值,此时则称之为“动态面板模型”,其目的是处理内生性问题。动态面板模型发展分为3个阶段,第1阶段是由Arellano and Bond(1991)提出的差分GMM(difference GMM),第2阶段由Arellano and Bover(1995)提出水平GMM,第3阶段是Blundell and Bond(1998)将差分GMM和水平GMM结合一起进行GMM估计即系统GMM(System GMM)。SPSSAU默认当前提供差分GMM和系统GMM两种类型,多数情况下使用系统GMM法。需要注意的是,动态面板模型通常只针对‘大N小T’这样的面板数据,如果T过大这会导致滞后项很多,待估计参数值可能过多无法拟合等。
动态面板模型时,通常会涉及到几种变量,分别说明如下:
系统GMM在选择被解释变量的几期滞后项作为解释变量时,一个原则是一直到第几期还显著,就用到第几期。例如,被解释变量的2期滞后项作为解释变量,2滞后项都显著,但加上3期滞后项后第2期不显著,第1和2期仍然显著,则一般只使用滞后的1和2期作为解释变量,不能用3期。并且必须用1和2期,不能只用1期或2期。因为结果表明1期和2期都显著,如果只用1期或2期,则会人为造成遗漏变量。
系统GMM在选择被解释变量和解释变量的几期滞后项作为IV时,有较大选择空间。只要能满足系统GMM的两个检验就行。系统GMM的两个检验是Hansen过度识别检验和扰动项无自相关AR检验,Hansen过度识别检验研究是否工具变量均为外生变量,如果其对应的p值大于0.05则意味着工具变量均外生,与此同时还需要通过AR检验,AR检验扰动项是否无自相关性,一般来说AR(2)对应的p值>0.05则接受原假设意味着模型通过自相关检验。动态面板模型构建时,工具变量参数的设置尤其复杂,但无论如何均需要通过Hansen过度识别检验和AR检验,才意味着模型可用,因而建议实际研究中让SPSSAU自动进行参数配置,即设置参数时让系统自动识别寻找最佳模型,当SPSSAU无法自动找出最优模型时,此时结合自身数据及专业实际情况进行逐一参数设置和调整。
1 背景
当前有一份595名美国工人1976-1982年关于工资的面板数据(N=595,T=7),涉及数据包括被解释变量:工资对数;另外包括11个解释变量,分别为:工龄,工作周数,是否蓝领,是否制造业工作,是否美国南方,是否住大城市,是否结婚,是否女性,是否工会,教育年限,是否黑人等。部分数据如下:
2 理论
动态面板数据是处理内生性问题的一种方法,将被解释变量的滞后项作为解释变量纳入模型,并且设置工具变量,进而进行估计,其工具变量的设置较为复杂,但需要尤其注意两个检验,分别是Hansen过度识别检验和扰动项无自相关AR检验。
3 操作
本例子中操作截图如下,使用系统GMM法和GMM差分使用OneStep法。下图中‘压缩工具变量’指将工具变量个数进行压缩减少,当研究变量过多并且工具变量可能很多时,可选中该项,本案例暂不选中该项。
关于‘设置数据’,首先动态面板时,被解释变量的滞后阶数会作为解释变量,那么具体滞后多少阶呢?这个可以自行设置(比如设置为滞后1阶~滞后2阶),当然也可以‘智能识别’,即系统会自动运行不同的滞后阶数参数值,并且结合Hansen过度识别检验和AR检验的结果,最终确定最优滞后阶数。与此同时,解释变量的滞后阶数也可以作为解释变量,但实际研究中很少有此类情况,因而解释变量的滞后阶数0阶到0阶,即不会纳入其滞后阶数到模型中。
除此之外,接着是工具变量设置,工具变量的设置上较为复杂,默认情况下以尽可能多的滞后阶数作为工具变量,具体实际研究时,可自行修改设置,但需要注意一点是,建议可先让系统默认即将所有可滞后的阶数纳入模型中,让系统判断是否通过Hansen过度识别检验和AR检验,如果通过也可,如果不通过建议此时结合专业知识情况进行逐一设置。
最后下图中‘时间项哑变量放入模型’,其是指将时间项处理成哑变量并且纳入模型中,默认不选中该项,如果需要可选中即可。
4 SPSSAU输出结果
动态面板模型一共输出5个表格,说明如下:
5文字分析
上表格展示模型信息,包括GMM类型,OneStep或TwoStep差分,信息准则aic值、bic值、hqic值等。并且展示模型代码,模型代码中L表示滞后阶数,比如L1表示之后1阶。Gmm表示gmm式工具变量,括号里面‘1:.’表示滞后1阶到全部阶数,如果是IV式工具变量则格式为iv(分析项),如果有压缩工具变量则会有‘collapse’参数值。上表格中展示 工具变量个数,总样本量,时间项,组别数量等信息,其受到工具变量等滞后阶数,是否压缩工具变量等参数影响,其并不特别意义。
如果在参数中被解释变量的滞后阶数为‘智能识别’(或解释变量滞后阶数也纳入模型,此时也有‘智能识别’,但通常解释变量较少将滞后阶数纳入模型),系统会运行多个模型然后对比,选择最优模型输出,其标准为通过Hansen过度识别检验和AR检验的最优模型。上表格中展示 智能识别滞后阶数成功,也即意味着当前模型通过Hansen过度识别检验和AR检验。
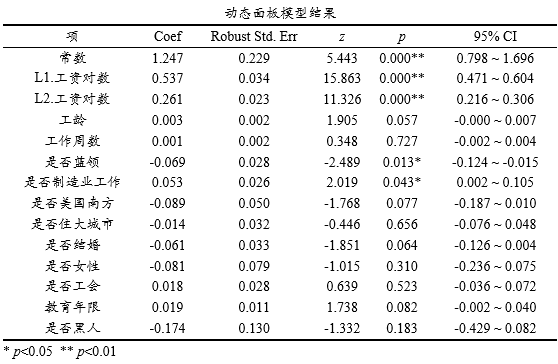
上表格展示动态面板模型结果,与普通的回归解释保持一致,先查阅某项是否呈现出显著性,如果呈现出显著性则再查阅回归系数Coef值,大于0则为正向影响,小于0则为负向影响。另外本次案例时被解释变量的滞后1阶和滞后2阶被纳入模型中,该两项均呈现出显著性。与此同时,是否蓝领和是否制造业工作这两项均呈现出显著性,是否蓝领的回归系数为-0.069<0,意味着蓝领的工作相对较低,并且是否制造业工作这项的回归系数值是0.053>0,说明制造业工作的工人其工作相对更高。
针对Hansen过度识别检验,其原假设是工具变量与误差项不相关,从上表格可知:模型拒绝HanSen过度识别检验(p=0.992>=0.05),意味着工具变量与误差项无关,说明当前模型构建良好。
AR根检验原定假设为模型不存在自相关关系,通常针对AR(2)检验即可,如果AR(2)对应的p值>0.05则接受原假设意味着模型通过自相关检验,反之则拒绝原假设意味着模型存在自相关关系。从上表格可知:模型接受AR(2)检验(p=0.063>=0.05),意味着模型不存在自相关性,说明当前模型构建良好。
另外SPSSAU还输出简化格式的动态面板模型结果表格,用于放入报告直接使用。
6 剖析
动态面板模型分析涉及以下几个关键点,分别如下:
- 动态面板模型适用于大N小T的数据结构,如果面板数据中时间项过长,比如30年的数据,这容易导致工具变量滞后阶数非常多,工具变量个数非常多从而影响模型构建;如果是T较长,建议使用普通的面板模型进行研究即可;
- 被解释变量滞后阶数设置上,建议选择‘智能识别’,让系统自动运行不同的滞后阶数对比选择最优模型;
- 工具变量设置上,默认是滞后1阶到全部阶数,这样工具变量个数会很多,建议可选择压缩工具变量个数等参数,也或者结合自身专业知识设置滞后阶数。