9.19数电——触发器&状态机&第四周作业题解&计数器(部分)
触发器
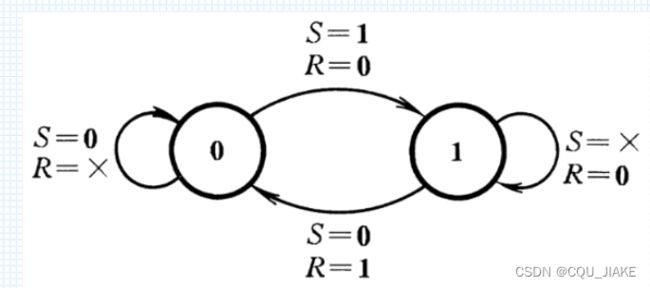
RS
1.输出置0 2.置1 3.输出保持不变
S:是置位信号,为1时说要置为1;为0时要置为0;
R:是复位信号,为1时就要无条件置为0,为0时保持寄存器原状态
如果要置为0,必要条件是R=1
要么置位,要么复位,所谓置位,就是置为1,没有说置为0的说法,复位才是所谓的置为0
故而不能同时有S,R信号
有S就是要置为1(置位),那么R必须为0
有R就是要置为0(复位),那么S必须为0
都是变化时作用,变化后就不变了(导数为0了)
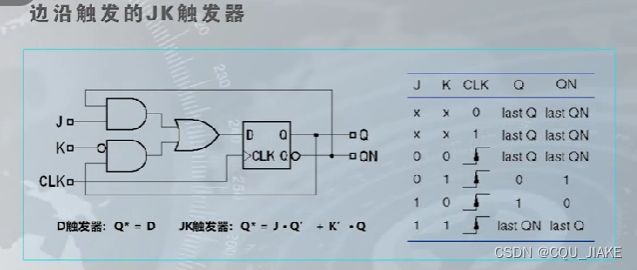
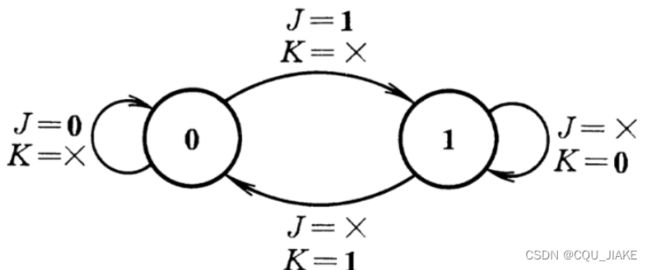
JK触发器
反转只发生在负跳边沿
此时,J就是置1信号,K就是置0信号
都为0时就保持
D:
D就是置位信号,D是多少就置为多少
记忆功能,具有两个稳定状态
电平触发:CP=1
边沿触发:正跳变0-1
次态取决于触发前的状态,具有置0,置1两种功能
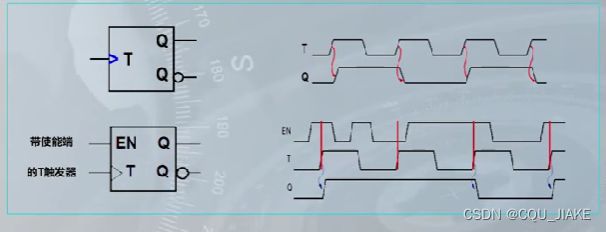
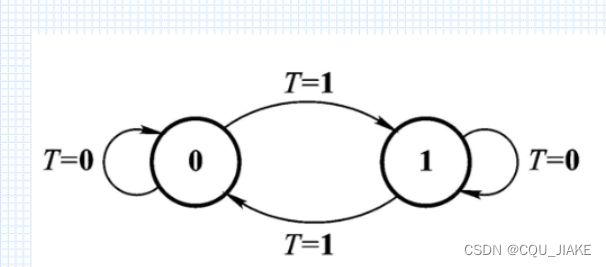
T触发器
这么想时钟沿,就是一个按钮,按一次clk就上升(即按的瞬间,信号接通的瞬间),然后保持按的时候就是clk一直处于1状态(一直按不松手),然后松手不按了,就使得clk下降,即没有按压信号输入了,clk就从1变到了0,即一次下降沿到来
下降沿来临时,rst就该发挥作用复位了
T触发器就是按一次按钮就计一次(反转一次),只计按的时候,松手的时候(松手的时候复位)不记录,故是说计数器,计按的次数
计数器,时钟周期到来,上升沿实现对原状态的反装
T触发器是进入值为1时,寄存值发生反转
T为0时保持原态,T为1时反转原态,
两个参数,一个是输入信号,一个是T(控制信号,决定是保持还是反转输入信号)
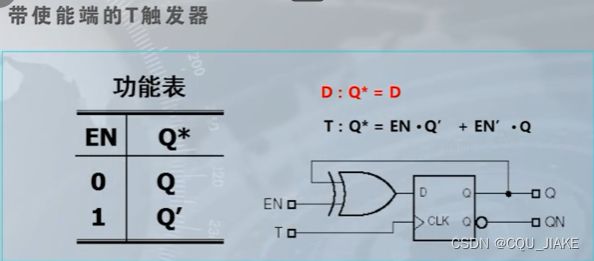
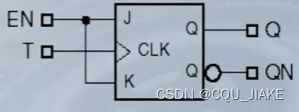
T触发器的实现
D触发器实现是说,让下个Q变成当前Q的非,那么就应该让D变为Q非,所以D端的输入信号为Q非后的信号
?Q的信号从哪来?
?clk信号到底扮演了一个怎样的角色?
T触发器:下一个Q是直接这个Q的非(反转一次)
用D触发器实现,就是让使能端和Q异或
module t(clk,rst,T,Q);
input clk,rst,T;
output reg Q;
always@(posedge clk or negedge rst)
begin
if(!rst)
Q<=1'b0;
else if(T)
Q<=~Q;
else
Q<=Q;
end
endmodule
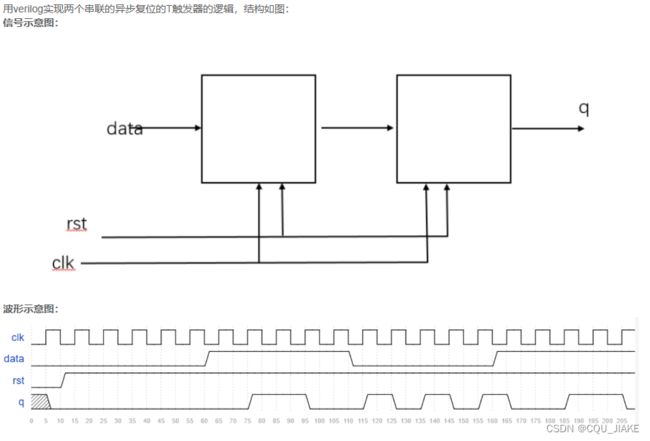
异步复位串联T触发器
这里第一寄存器,第二寄存器的T信号均为clk,即data有信号时
在data有值之前,第一寄存器保持为clk的值,有值后,反转clk的值
第一寄存器在data作用下处理完clk信号后,输出一个信号,作为第二寄存器的data信号
第二寄存器是否反转取决于第一个寄存器是否为1
前者输出有三种:在data输入控制为1下,从0到1,1到0不断反转,data为0时,锁在1
当clk上升且T信号(data)为1时,信号发生反转
q1是q2的T信号,当q1是1时,q2才会发生反转
data为0时保持,保持的是自己之前的信号,而不是保持时钟的
触发器
就是反转器,其自己存个信号,然后根据连接的信号,不断反转自己的信号,得到一个输出
rst
转化为低电平复位,高电平不作用,为1时表示完成初始化,电路正常运作
就是工作时是1,然后工作结束了,一关,rst从1变到0,就完成了一次复位,所以要用negedge
状态机
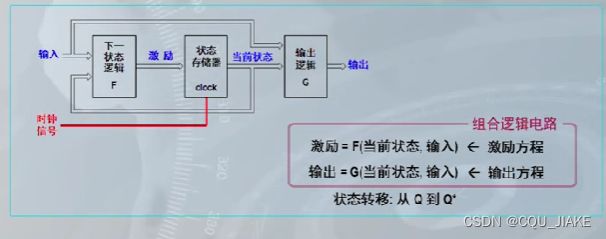
时钟信号扮演了一个怎样的角色?
由同一个时钟信号控制,则为同步;否则为异步
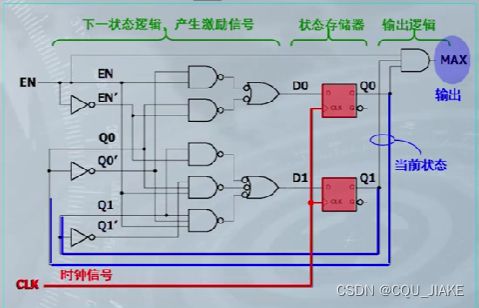
一个Q0,可以直接接在输入端,也可以通过非门后接到输入端
激励不等于状态,激励(D)由输入信号产生,状态(Q)由激励确定
输入信号就相当于自变量,产生激励就相当于经过一个函数处理,状态就是最后的因变量
(更贴切的可以理解为分段函数,激励就是传入x后都进行处理,即每段都有x进行处理,然后最后选择因变量就是根据x到底在哪一段,从这些分段函数所产生的结果中选择出对应的结果)
(也可以理解成是表达式中的某一项,这一项出现的频次非常高,就相当于换元,把这个作为一个激励,然后整进去表达式里)
上个状态可以作为输入信号来产生对下个状态的激励
激励怎么来的?
由电路图导出激励方程(确定每个触发器输入端的信号),
然后由触发器的组合,确定输出方程(由触发器的耦合确定最后实现什么功能)
最后绘制时序图
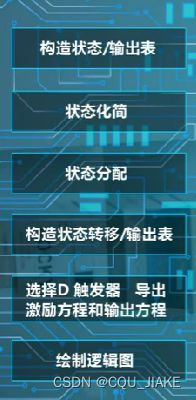
a.设计计数器
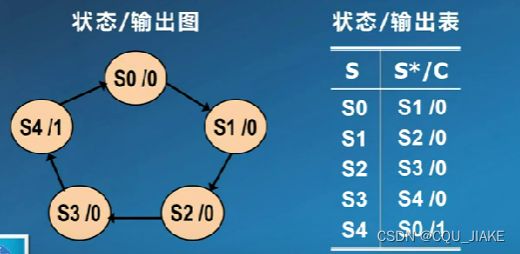
1.设计状态表&2.状态化简
只有记到4时,才输出一个1
3.状态分配
根据状态总数确定该用多少个状态分码(状态变量Q0,Q1……)来组合,如这里有5种状态,所以至少需要用3个状态码(Q0,Q1,Q2)来组合,才能表示出所有情况
用格雷码编码状态编号,即先用二进制依次编好,再转换为对应的格雷码,目的是为了方便后续的卡诺图求解方程
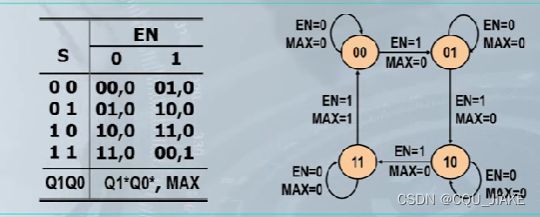
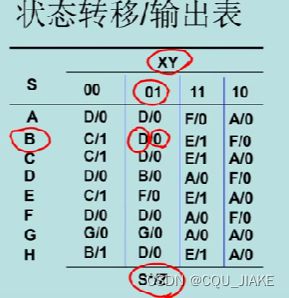
4.构造状态转移/输出表
单独的状态变量不能表示任何含义,组合在一起才能表示出一个状态的编号,状态的编码与排序是认为规定的,如Q0,Q1,Q2组合成的000就表示一种状态,只知道Q1,Q0,Q2中的一个或两个就不能完整确定一个状态,只能猜个大概。
排序并不一定要遵循从小到大,用格雷码排可以更好地由卡诺图求解方程(上图并非格雷码与卡诺图)
格雷码怎么确定排序?
对于未用状态?
对于未用状态,最小风险设计:就转为初始状态(常用且好用,就是卡诺图里不会出现的情况直接当成0处理)
最小成本法:要保证未用状态就不会出现
绿色表示未用状态
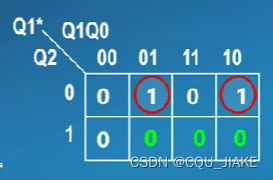
这个表是关于Q2的次态与Q2,Q1,Q0的关系,一共需要确定三个(即Q2,Q1,Q0分别的次态)
最终确定为Q2*=!Q2&Q1&Q0
Q1*=!Q2&!Q1&Q0+!Q2&Q1&!Q0
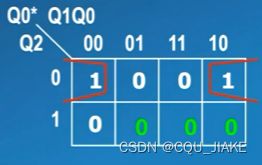
Q0*=!Q2&!Q0
5.选择触发器类型
绝大多数用D触发器
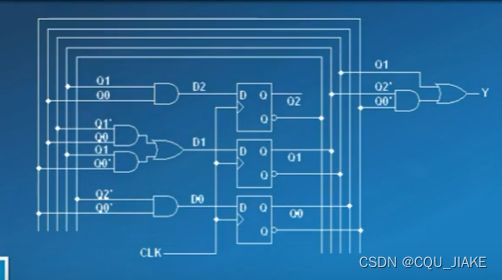
6.根据前面的步骤给出电路图
另:修改输出即可从计数器转为10110序列产生器
b.序列检测器(1101):
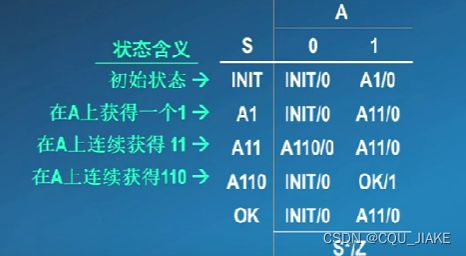
1.设计状态表
下一状态&输出
每个时刻都有多个状态变量
2.状态化简
A1与OK的输入与下一状态相同,消掉ok,
3.状态分配
格雷码,用编码表示状态
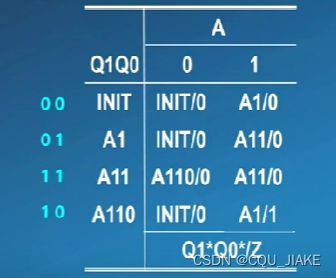 Q1Q0就是表示状态的码,单独一个Q没有任何意义,只有Q组合在一起才能完整表示一种状态,状态的总数量取决于Q的数量(或者可以说是Q的数量由状态的总数量决定,即有多少种状态就需要用多少个Q来组合表示)
Q1Q0就是表示状态的码,单独一个Q没有任何意义,只有Q组合在一起才能完整表示一种状态,状态的总数量取决于Q的数量(或者可以说是Q的数量由状态的总数量决定,即有多少种状态就需要用多少个Q来组合表示)
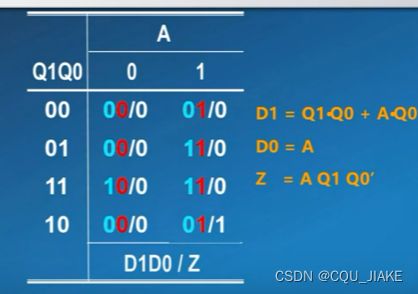
4.构造状态转移输出表
5.选触发器,构造方程
选用D触发器,则Q(单独的状态编码)=D,即Q1=D1,Q0=D0
每个状态编码都需要有一个激励来确定,即有Q0Q1,就需要有D0D1来去确定Q0Q1
只看红的可以发现,Q0与A一致,又Q0=D0,所以可以写D0=A;
只看蓝的,就用卡诺图化简,得到表达式
D1包含A*Q0,就说明只有Q0为1且A为1时,才能输出Q1的次态为1
在输出1时,Q1,A为1,Q0为0,所以Z=A*Q1*!Q0
小总结:
既然状态是用Q1,Q0拆开表示,那怎么把Q1,Q0再合并起来表示一个对应的状态?
通过与,就是只有Q1,Q0是某个特定的值(组合拼接在一起就是所对应的状态编号),与在一起,才为1,不然,只要有一个不是目标状态的编号(所拆分出来的),那就与不出来1,也就输出不了1;
即只有需要对应情况的输出时,把那种情况的状态变量与在一起,进行输出
而对于状态间转移,不需要拼在一起(即进行与的处理),就让各个分编码按照卡诺图求出的规则进一步变化(就是从当前状态(一组Q)变到了另一种状态(后一组Q))即可
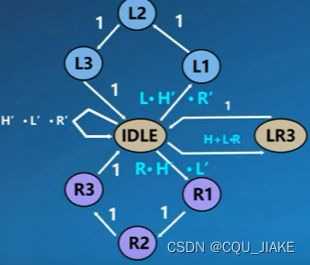
题解:尾灯控制
1.设计状态表&2.状态化简
根据实际问题,题意,目标确定,
状态表,输入输出表,描述状态之间的转变
应满足互斥性与完备性
互斥性
离开某个任意状态的所有箭头(伸出的箭头,出度)的逻辑积(与操作)为0
即不能都为1,得有0;不然则伸出的箭头都表示必须转移的状态,接下来状态就不确定
完备性
离开某个任意状态的所有箭头的逻辑和(或操作)为1
即不能都为0,得有1,不然到这个状态后就转不出去,钉死在这个状态了
L与R都为1,不满足互斥性
3.状态分配
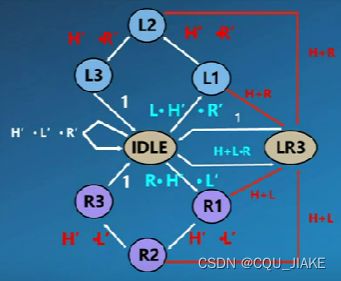
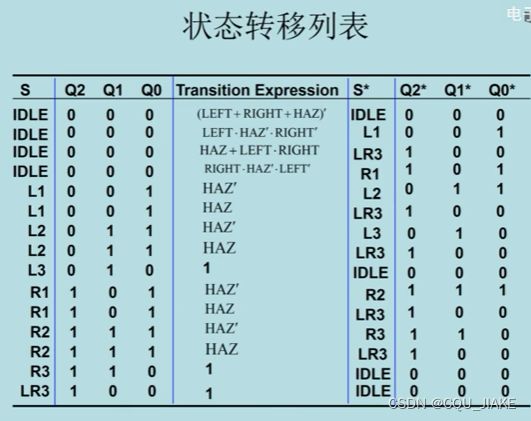
4.构造状态转移/输出表
得到状态转移方程,还可以直接在原状态的基础上与上转移表达式
即次态Q(某个)=原状态Q(一组,表示当前的特定状态)&转移表达式(由输入信号的参数决定)
题解:小鼠煮咖啡
由于移动方向只有向前或向后两种情况,所以实际应当是小鼠固定在槽形上前后移动
漕渠的一头终点就是咖啡机所在位置,如果不在相应的位置,小鼠就无法制作咖啡
那么位置就存在两种状况,即靠近咖啡机所在位置及不靠近咖啡所在位置
分别定义为X——还需要移动才能到达咖啡机所在位置,即不靠近的情况
与Y——不需要移动,即已经位于咖啡机所在位置
D——表示正在注入咖啡的过程
E——表示注入结束,即可以保证咖啡杯里至少是有咖啡的一个状态
ON——开火,即正在烧咖啡的状态
那么处于X时,只有前进指令(F)才能使它到达咖啡机的位置;不然如果是后退(B),就更不能使小鼠到达位置。其他指令在此阶段均无效,保持X状态。
一旦执行了前进或后退,那么在前进或后退过程(即原A,B所描绘的正处于前进或后退状态)中时,不再接受新指令,直到当前移动指令结束,即要么从漕渠的另一头到咖啡机,要么从咖啡机移动到漕渠的另一头(可以考虑添加停止的指令,使小鼠停在漕渠的任一位置)。
处于Y时,如果执行后退指令,就又回到了X;如果执行加咖啡指令,则进入D状态;其他指令在此阶段均无效,保持Y状态。
处于D时,只有S指令才能终止加咖啡的状态,进入E状态;其他指令在此阶段均无效
考虑到制作咖啡需要认真专注,所以一旦加入咖啡,就不允许小鼠再离开咖啡机的位置(其实可以设计为离开,这里为了安全,选择不离开,即D之后的状态对于B指令均无效)
处于E时,可以认为咖啡没加够,或者就是还想加,加到溢满,即依然可以执行I指令,继续加咖啡,进入D状态;也可以认为加够了,直接开始制作,执行TUON指令,进入ON状态
处于ON状态时,只有TUOF指令才可以关闭火焰,进入Y状态,并输出1,表示制作完成。其他指令均无效。
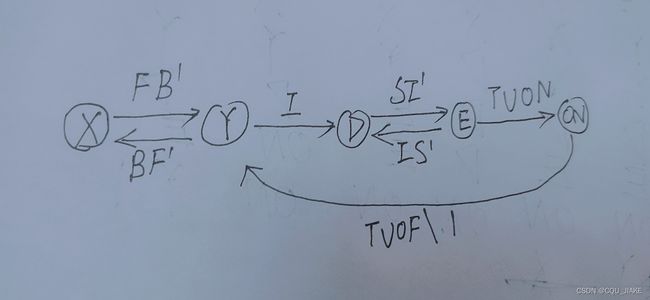 关于结束后进入Y状态:认为制作完成后,应将机器里的咖啡全部取出,即此时机器里没有咖啡,需要重新注入,执行I指令,即不进入E状态。或者制作完成后,小鼠可以选择执行B指令,离开咖啡机。
关于结束后进入Y状态:认为制作完成后,应将机器里的咖啡全部取出,即此时机器里没有咖啡,需要重新注入,执行I指令,即不进入E状态。或者制作完成后,小鼠可以选择执行B指令,离开咖啡机。
编码状态X,Y等状态,并根据转移方式,得到表达式
再接着就是选择触发器去实现接收信号转化为激励,并由激励转化为状态,来设计电路。
一种简单的方式就是采用D触发器,令D=Q,直接构造。
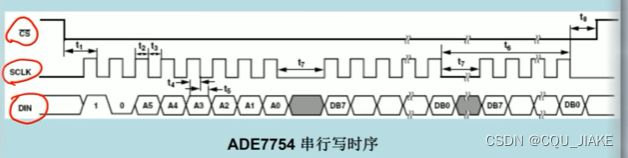
时序逻辑标准文档
原理框图,原理图,程序源代码,状态图,时序图,状态转移列表
计数器
T触发器
每次时钟上升沿到来就反转一次,只有反转,没有复位
即第一次时钟上升沿到了,从0——1,第二次上升沿到了,才有1——0
只有上升沿来了才反转,只有上升沿来了才反转,只有上升沿来了才反转
即两个时钟周期一次复位,故又名为模二计数器
行波计数器
异步
从低位到高位代表Q0,Q1,Q2,Q3
时序图上为高电平,就代表对应位上为1
Qn上升沿来一次,就代表Qn-1下降沿到来,即Qn-1从1到0,可以看成发生了进位,即使Qn-1加1的操作发生了两次,Qn-1记录不了,就用一位Qn来记录
Qn下降沿来一次,就代表Qn-1下降沿来了两次
一次Qn-1下降沿使Qn转为上升沿进到1,一次Qn-1下降沿使Qn转为下降沿,从1到0
0001,0010,0011,0100,0101,0110,0111,~1001(发生这种情况的原因是越向下Q的延时就越大,导致在Q4进位时,Q0已经因为时钟上升沿的到来进位了,导致电路丢失了1000的状态,直接进入到了1001的状态)
在时钟上升沿来临时,Q0反转,即从0——1,
再次来临时,Q0反转,从1——0,相当于每次时钟上升沿来临,都是Q0加了一位
那么Q0下降,即从1——0时,应当进位,即Q1从0——1
Q0有下降沿,就说明时钟上升沿来了2次,
那么有两次时钟下降沿就有Q1反转一次
同理Q1有下降沿就说明Q0下降沿来了两次(Q1反转两次),时钟上升沿来了四次
Q1有下降沿时,Q2反转一次,
Q2有下降沿时,Q1下降沿来了两次,Q0下降沿来了4次,时钟上升沿来了8次
Q3有下降沿时,Q2下降沿来了两次,Q1下降沿来了4次,Q0下降沿来了8次,时钟上升沿来了16次
即都是每两个上级周期一次反转复位,完成该级的一次周期
同步计数器
同步,即时钟信号都相同
并行使能的使能端同步进行,无递推,最快
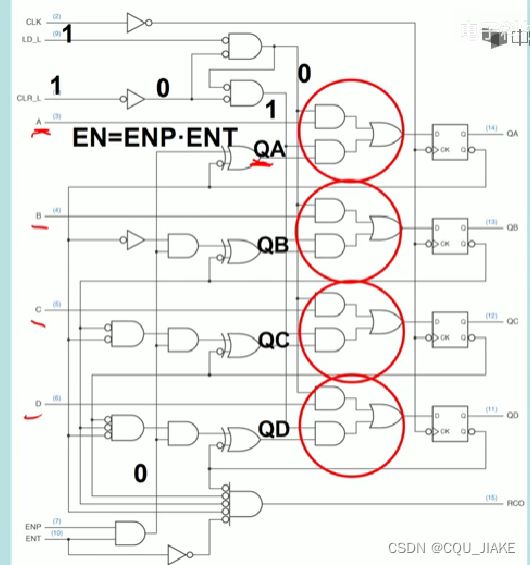
二进制计数器
当CLR_L为0时,通过非门变成1,再通过非与门变成0,传递到后面的与门,使其输出均为0,即所谓同步清零
当清零信号为1时,过非门为0,对后面的非与门不起作用,起作用的就是LD_L,如果LD_L为0,则上面的非与门出来就是1,又作为信号传到下面的非与门,使下个非与门的输出为0,下面的非与门输出为0会导致选择器的下面的与门后都是0,只有二选一选择器上面的与门能正常工作
如果LD_L为1,则上面的非与门后就是0,给到下面的非与门,其输出就是1,这会导致,在四个二选一选择器中,上面的与门都会接收到0信号,而下面的与门不受影响,继而完成选择
使能端为俩个使能信号的与,如果其中有一个为0,那么通过异或门后的值都为4个信号原始的值,说是状态保持,不计数状态
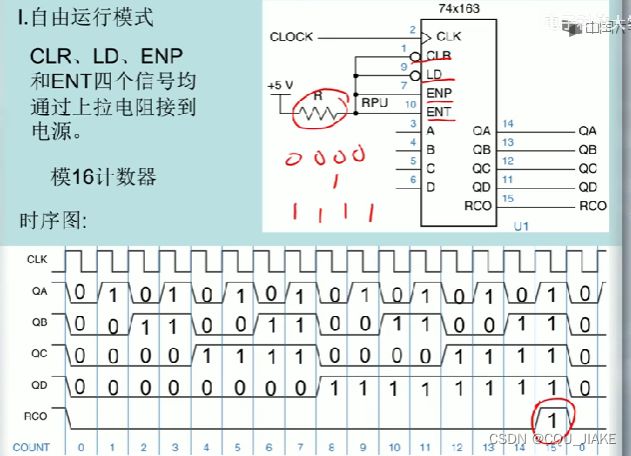
74x163
74163,CLR有效时,强制
反馈清零法
多次预置法