使用 PyTorch 的计算机视觉简介 (3/6)
一、说明
在本单元中,我们将了解卷积神经网络(CNN),它是专门为计算机视觉设计的。 卷积层允许我们从图像中提取某些图像模式,以便最终分类器基于这些特征。
二、卷积神经网络
计算机视觉不同于通用分类,因为当我们试图在图片中找到某个物体时,我们正在扫描图像以寻找一些特定的图案及其组合。比如在寻找猫的时候,我们首先可能会寻找水平线,可以形成胡须,然后一定的胡须组合可以告诉我们它实际上是猫的图片。某些图案的相对位置和存在很重要,而不是它们在图像上的确切位置。为了提取模式,我们将使用卷积过滤器的概念。但首先,让我们加载之前定义的所有依赖项和函数。
!wget https://raw.githubusercontent.com/MicrosoftDocs/pytorchfundamentals/main/computer-vision-pytorch/pytorchcv.py
import torch import torch.nn as nn import torchvision import matplotlib.pyplot as plt from torchinfo import summary import numpy as np from pytorchcv import load_mnist, train, plot_results, plot_convolution, display_dataset load_mnist(batch_size=128)
三、卷积滤波器
卷积滤波器是在图像的每个像素上运行并计算相邻像素的加权平均值的小窗口。它们由权重系数矩阵定义。
让我们看看在 MNIST 手写数字上应用两个不同的卷积过滤器的示例:
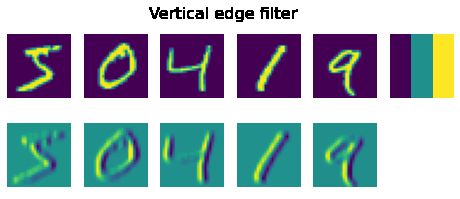
plot_convolution(torch.tensor([[-1.,0.,1.],[-1.,0.,1.],[-1.,0.,1.]]),'Vertical edge filter') plot_convolution(torch.tensor([[-1.,-1.,-1.],[0.,0.,0.],[1.,1.,1.]]),'Horizontal edge filter')
第一个过滤器称为垂直边缘过滤器,它定义为:
-1 0 1 -1 0 1 -1 0 1
当此过滤器经过相对均匀的像素字段时,所有值的总和为 0。但是,当它在图像中遇到垂直边缘时,会产生高峰值。这就是为什么在上图中,您可以看到由高值和低值表示的垂直边缘,而水平边缘则平均化。
当我们应用水平边缘滤波器时,会发生相反的事情,其中水平线被放大,垂直线被平均。
如果我们将 3 × 3 滤镜应用于大小为 28 × 28 的图像 — 图像的大小将变为 26 × 26,因为过滤器不会超出图像边界。但是,在某些情况下,我们可能希望保持图像的大小相同,在这种情况下,图像每边都填充零。
在经典的计算机视觉中,将多个过滤器应用于图像以生成特征,然后机器学习算法使用这些特征来构建分类器。然而,在深度学习中,我们构建的网络可以学习最佳的卷积过滤器来解决分类问题。
为此,我们引入了卷积层。
四、卷积层
卷积层使用 nn 定义。Conv2d 构造。我们需要指定以下内容:
- in_channels — 输入通道数。在我们的例子中,我们正在处理灰度图像,因此输入通道的数量为1。彩色图像有 3 个通道 (RGB)。
- out_channels — 要使用的过滤器数量。我们将使用 9 种不同的筛选器,这将为网络提供大量机会来探索哪些筛选器最适合我们的方案。
- kernel_size是滑动窗口的大小。通常使用 3 个× 3 个或 5 个× 5 个过滤器。过滤器尺寸的选择通常通过实验选择,即通过尝试不同的过滤器尺寸并比较结果的准确性。
最简单的CNN将包含一个卷积层。给定输入大小
28 × 28,在应用 5 个 5 × 9 个过滤器后,我们最终将得到 24 × 24 × 24 的张量(空间大小较小,因为只有 5 个位置,长度为 28 的
滑动间隔可以容纳 9 像素)。在这里,每个滤波器的结果由图像中的不同通道表示。因此,第一维<>对应于滤波器的数量。
卷积后,我们将 9 × 24 × 24 张量展平为一个大小为 5184 的向量,然后添加线性层,生成 10 个类。我们还在层之间使用 relu 激活函数。
class OneConv(nn.Module):
def __init__(self):
super(OneConv, self).__init__()
self.conv = nn.Conv2d(in_channels=1,out_channels=9,kernel_size=(5,5))
self.flatten = nn.Flatten()
self.fc = nn.Linear(5184,10)
def forward(self, x):
x = nn.functional.relu(self.conv(x))
x = self.flatten(x)
x = nn.functional.log_softmax(self.fc(x),dim=1)
return x
net = OneConv()
summary(net,input_size=(1,1,28,28))
========================================================================================== Layer (type:depth-idx) Output Shape Param # ========================================================================================== ├─Conv2d: 1-1 [1, 9, 24, 24] 234 ├─Flatten: 1-2 [1, 5184] -- ├─Linear: 1-3 [1, 10] 51,850 ========================================================================================== Total params: 52,084 Trainable params: 52,084 Non-trainable params: 0 Total mult-adds (M): 0.18 ========================================================================================== Input size (MB): 0.00 Forward/backward pass size (MB): 0.04 Params size (MB): 0.21 Estimated Total Size (MB): 0.25 ==========================================================================================
您可以看到,该网络包含大约 50k 的可训练参数,而在完全连接的多层网络中,则包含大约 80k 个参数。这使我们能够在较小的数据集上获得良好的结果,因为卷积网络的泛化效果要好得多。
请注意,卷积层的参数数量非常少,并且不依赖于图像的分辨率!在我们的例子中,我们使用了 9 个维度为 5 × 5 的过滤器,因此参数的数量为
9 × 5 × 5 + 9 = 234。尽管我们在上面的讨论中错过了这一点,但卷积过滤器也有偏见。我们网络的大部分参数来自最终的密集层。
hist = train(net,train_loader,test_loader,epochs=5) plot_results(hist)
Epoch 0, Train acc=0.947, Val acc=0.969, Train loss=0.001, Val loss=0.001 Epoch 1, Train acc=0.979, Val acc=0.975, Train loss=0.001, Val loss=0.001 Epoch 2, Train acc=0.985, Val acc=0.977, Train loss=0.000, Val loss=0.001 Epoch 3, Train acc=0.988, Val acc=0.975, Train loss=0.000, Val loss=0.001 Epoch 4, Train acc=0.988, Val acc=0.976, Train loss=0.000, Val loss=0.001
如您所见,与以前的全连接网络相比,我们能够实现更高的精度和更快的速度。我们还可以可视化经过训练的卷积层的权重,以尝试更有意义地了解正在发生的事情:
fig,ax = plt.subplots(1,9)
with torch.no_grad():
p = next(net.conv.parameters())
for i,x in enumerate(p):
ax[i].imshow(x.detach().cpu()[0,...])
ax[i].axis('off')
您可以看到其中一些过滤器看起来可以识别一些倾斜的笔划,而另一些则看起来非常随机。
五、小结
卷积层允许我们从图像中提取某些图像模式,以便最终分类器基于这些特征。但是,我们可以使用相同的方法来提取特征空间内的模式,方法是在第一个卷积层之上堆叠另一个卷积层。我们将在下一个单元中学习多层卷积网络。