动态规划法求解数塔的最优路径

使用动态规划法解决数塔问题。

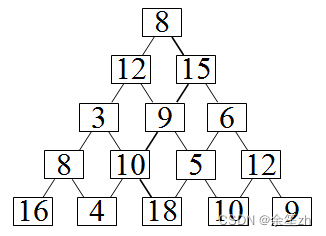
问题描述：从数塔的顶层出发，在每一个结点可以选择向左走或向右走，一直走到最底层，要求找出一条路径，使得路径上的数值和最大。

 将数塔看作为二维数组，一个数的左子树在下方，右子树在下方的右边。

8
12	15
3	9	6
8	10	5	12
16	4	18	10	9

辅助表格为sum二维数组，将数塔中的值从下往上考虑，对于每一层只需要考虑自己下面连接的左右两边哪个数大，将自身的值加上这个较大值，可以得到一个辅助表格。

60
49	52
31	37	29
24	28	23	22
16	4	18	10	9

然后从上往下考虑，根据辅助表格，选择较大数值对应的左右两边数，找到这个大的数对应的数塔中的数，存放在一维数组中并输出，得到了最优路径。最优路径为：

8

15

9

10

18

//问题：数塔求解最优路径

//输入：一个二维数组tower[size][size]，数塔数据存放在tower的下三角内。

//输出：辅助表格sum数组,一条最优路径存储在一维数组path[size]中，最优路径的长度。

//算法步骤：

//1.定义一个辅助表格sum[size][size]，存储数塔每个节点的最优路径数值和。

//2.初始阶段计算：将数塔tower最底层的size个节点值填入辅助表格sum的最底层对应位置。

  //2.1列号j从0到size-1，逐个处理。

  //2.2 sum[size-1][j]=tower[size-1][j]       

//3.行号i从size-2到0，列号j从0到i，逐行处理：

  //3.1将sum[i+1][j]和sum[i+1][j+1]进行比较

  //如果sum[i+1][j]大，sum[i][j]=sum[i+1][j]+tower[i][j]

  //如果sum[i+1][j+1]大，sum[i][j]=sum[i+1][j+1]+tower[i][j]

//4.输出辅助表格sum

  //4.1行号i从0到size-1，列号j从0到i

  //4.2依次输出sum中的数        

//5.定义最优路径数组path[size]，初始path[0]=tower[0][0]。初始较大数值列号x=0

//6.行号i从1到size-1，列号j从0到i，逐行如下处理：

  //5.1 比较sum[i][x]和sum[i][x+1]大小

  //5.2如果sum[i][x]大，path[i]=tower[i][x]

  //5.3如果sum[i][x+1]大，path[i]=tower[i][x+1]

  //5.4将较大数值对应的列号j赋值给x

//7.输出path数组,最优路径的长度

import java.util.Arrays;
//问题：数塔求解最优路径
//输入：一个二维数组tower[size][size]，数塔数据存放在tower的下三角内。
//输出：辅助表格sum数组,一条最优路径存储在一维数组path[size]中，最优路径的长度。
public class Tower {
    static int size=5;
    public static void main(String[] args) {
        int[][]tower={{8,0,0,0,0},
            {12,15,0,0,0},
            {3,9,6,0,0},
            {8,10,5,12,0},
            {16,4,18,10,9}};
        int[][]sum=new int[size][size];//存储数塔每个节点的最优路径数值和。
        int[] path=new int[size];//最优路径
        int x=0;//较大数值对应的列号
        //将数塔tower最底层的size个节点值填入辅助表格sum的最底层对应位置。
        for(int j=0;j=0;i--){
            for(int j=0;j<=i;j++){
                if(sum[i+1][j]>sum[i+1][j+1]){
                    sum[i][j]=sum[i+1][j]+tower[i][j];
                }else{
                    sum[i][j]=sum[i+1][j+1]+tower[i][j];
                }
            }
        }
        //输出sum数组中不为0的数
        System.out.println("辅助表格:");
        for(int i=0;isum[i][x+1]){
                    path[i]=tower[i][x];
                }else{
                    path[i]=tower[i][x+1];
                }
                x=j;
            }
        }
        System.out.println("最优路径为："+Arrays.toString(path));
System.out.println("最优路径的长度为："+sum[0][0]);
    }
}

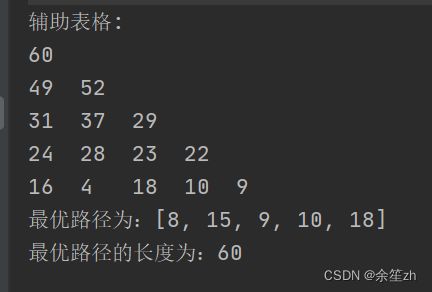
 输出辅助表格sum数组，一条最优路径和最优路径的长度，如图所示：