图的存储(邻接矩阵,邻接表,十字链表)
文章目录
- 前言
- 一、邻接矩阵
-
- 1.无向图的邻接矩阵
- 2.有向图的邻接矩阵
- 3.网图的邻接矩阵
- 4.算法实现
- 二、邻接表
-
- 1.无向图的邻接表
- 2.有向图的邻接表
- 3.网图的邻接表
- 4.算法实现
- 三、十字链表
-
- 1.有向图十字链表
- 2.算法实现
- 四、邻接多重链表
- 总结
前言
提示:以下是本篇文章正文内容
一、邻接矩阵
图的特点: 顶点之间的关系是m:n,即任何两个顶点之间都可能存在关系(边),无法通过存储位置表示这种任意的逻辑关系,所以,图无法采用顺序存储结构
邻接矩阵(数组表示法)
基本思想:用一个一维数组存储图中的顶点的信息,用一个二维数组(称为邻接矩阵)存储图中各顶点之间的邻接关系
假设图G = (V,E)有n个顶点,则邻接矩阵是一个n x n的方阵, 矩阵的值:
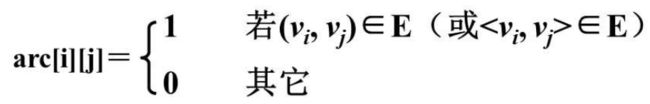
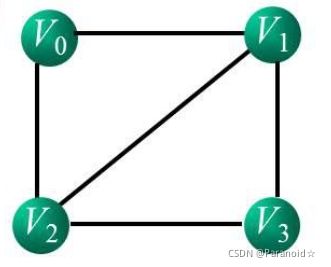
1.无向图的邻接矩阵

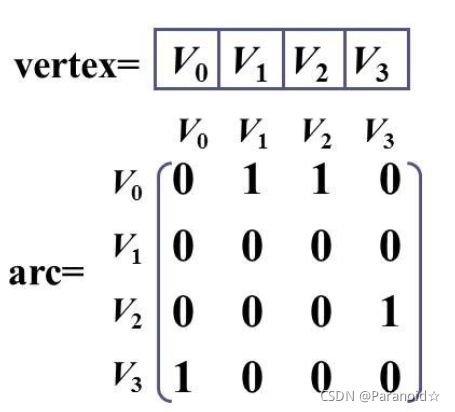
邻接矩阵如图

无向图的邻接矩阵主对角线为0且一定是对称矩阵(两个顶点之间共用一条边),arc[i][j]=1,则说明顶点i和j之间存在边
顶点i的度: 邻接矩阵的第i行或者第i列非零元素的个数,V1的度为3
2.有向图的邻接矩阵
顶点i的出度:邻接矩阵第i行元素之和
顶点i的入度:邻接矩阵第i列元素之和
3.网图的邻接矩阵
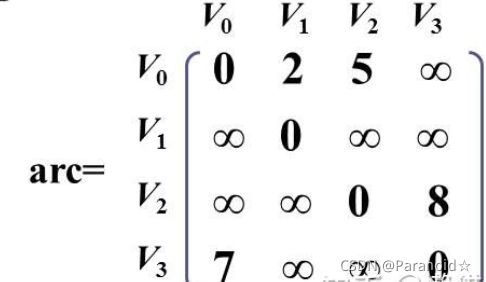
网图(带权的图)的邻接矩阵定义

若两个顶点存在关系,wij就等于该边的权值,若不存在关系则为无穷大

邻接矩阵如图
4.算法实现
无向图邻接矩阵类的定义
const int MAX_VERTEX = 10; // 图的最大顶点数
class MGraph
{
private:
DataTpye vertex[MAX_VERTEX]; // 顶点数组
int arc[MAX_VERTEX][MAX_VERTEX]; // 邻接矩阵
int vertexNum,arcNum;
public:
MGraph(DataTpye v[],int n,int e); // 图的构造函数
~MGraph(); // 图的析构函数
void DFSTraverse(int v);
void BFSTraverse(int v);
}
邻接矩阵构造函数
// 邻接矩阵构造函数
MGraph::MGraph(DataTpye v[],int n,int e) //n顶点数,e边数
{
vertexNum=n; //顶点数
arcNum=e; //边数
for(int i=0;i<vertexNum;i++) //顶点数组
{
vertex[i]=v[i]
}
for(int i=0;i<vertexNum;i++) //初始化邻接矩阵
{
for(int j=0;j<arcNum;j++)
{
arc[i][j]=0;
}
}
for(int i=0;i<vertexNum;i++) // 依次输入每条边
{
cin>>vi>>vj; // 输入边依附的两个顶点的编号
arc[vi][vj]=1; // 置有边标志
arc[vj][vi]=1;
}
}
实现过程:
1.确定图的顶点个数和边的个数
2.输入顶点信息存储在一维数组vertex中
3.初始化邻接矩阵arc
4. 依次输入每条边存储在邻接矩阵arc中
4.1输入边依附的两个顶点的序号i, j
4.2将邻接矩阵的第i行第j列的元素值置为1
4.3将邻接矩阵的第j行第i列的元素值置为1
二、邻接表
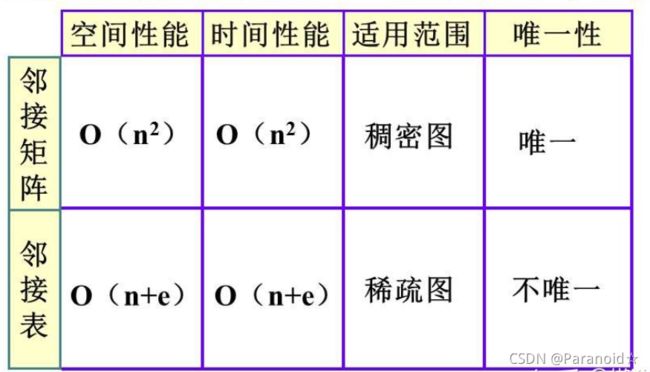
图的邻接矩阵存储结构,假设图G有n个顶点e条边,则存储结构的空间复杂度O(n2), 若存储稀疏图会浪费大量的存储空间
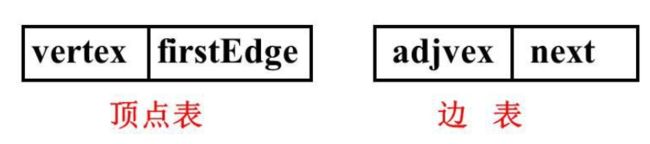
邻接表存储的基本思想: 对于图的每个顶点vi,将所有邻接于vi的顶点链成一个单链表,称为顶点vi的边表(对于有向图则称为出边表),所有边表的头指针和存储顶点信息的一维数组构成了顶点表
vertex:数据域,存放顶点信息
firstEdge:指针域,指向边表中的第一个结点
adjvex: 邻接点域,边的终点在顶点表中的下标
next:指针域,指向边表的下一个结点
// 边表
struct ArcNode
{
int adjvex;
ArcNode* next;
}
// 顶点表
struct VertexNode
{
DataTpye vertex;
ArcNode* fiestEdge;
}
1.无向图的邻接表

链表:
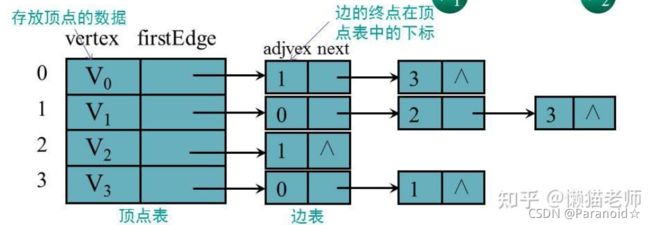
注: 在边表中存放的是与顶点表中的顶点有关系的顶点的在顶点表中的下标,边表中的每一个结点对应于图中的一条边,所以,顶点i的度为顶点i的边表中的结点的个数,邻接表的空间复杂度为O(n+e)
判断顶点i和顶点j是否存在边:顶点i的边表中是否存在终点为j的结点
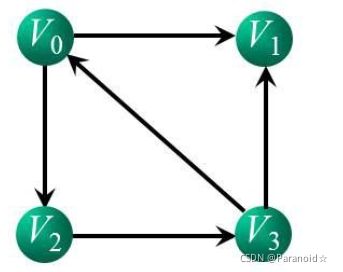
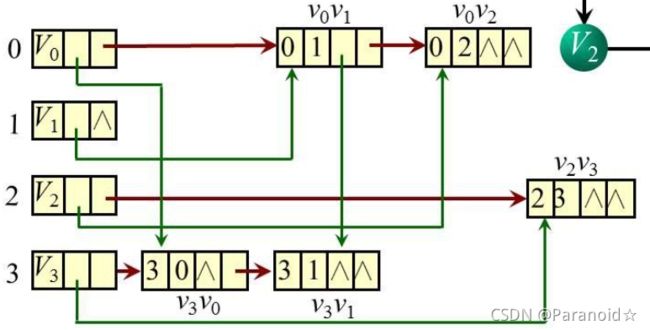
2.有向图的邻接表
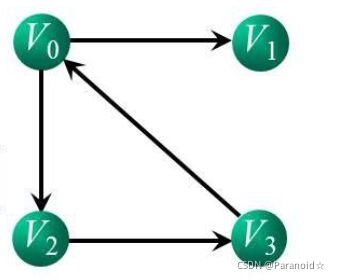
邻接表:

顶点i的出度:顶点i的出边表中的结点个数
顶点i的入度:各顶点的出边表中以结点i为终点的结点个数
V0的出度:2 ,入度: 1
求顶点i的所以结点:遍历顶点i的边表,该边表中的所有顶点都是顶点i的邻接点
3.网图的邻接表
4.算法实现
邻接表有向图的类
// 边表
struct ArcNode
{
int adjvex;
ArcNode* next;
}
// 顶点表
struct VertexNode
{
DataTpye vertex;
ArcNode* fiestEdge;
}
const int MAX_VERTEX = 10; // 图的最大顶点数
class ALMGraph
{
private:
VertexNode adjList[MAX_VERTEX]; // 顶点表
int vertexNum,arcNum;
public:
ALMGraph(DataTpye v[],int n,int e); // 图的构造函数
~ALMGraph(); // 图的析构函数
void DFSTraverse(int v);
void BFSTraverse(int v);
}
邻接表的构造函数
ALMGraph::ALMGraph(DataTpye v[],int n,int e)
{
vertexNum=n; //顶点数
arcNum=e; //边数
for(int i=0;i<vertexNum;i++)
{
// 输入顶点数据,并初始化顶点表
adjList[i].vertex=v[i];
adjList[i].fiestEdge=NULL;
}
for(int i=0;i<vertexNum;i++)
{
//输入边的存储信息在边表中
cin>>vi>>vj; // 输入边依附的两个顶点编号
s = new ArcNode;
s->adjvex=vj; // 插入边表结点
s->next=adjList[vi].firstEdge;
adjList[vi].firstEdge=s;
}
}
实现过程:
1.确定图的顶点个数和边的个数
2.输入顶点信息,初始化该顶点的顶点表
3.依次输入边的信息并存储在边表中
3.1输入边所依附的两个顶点的序号vi和vj
3.2生成邻接点序号为vj(边的终点)的边表结点s
3.3将结点s插入到第vi个边表的头部
三、十字链表
十字链表是将邻接表和逆邻接表合二为一(逆邻接表中,边表的的结点是弧的起点)
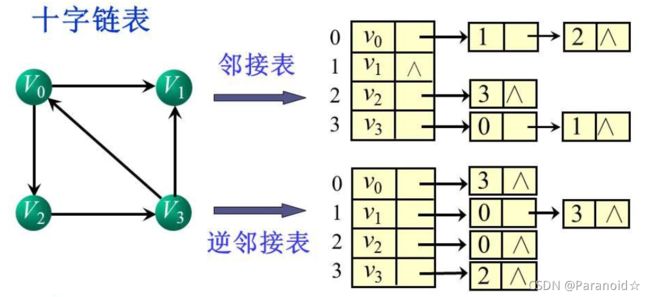
vertex:数据域,存放顶点信息
firstin:入边表头指针
firstout:出边边头指针
tailvex:弧的起点在顶点表中的下标
headvex:弧的终点在顶点表中的下标
headlink:入边表指针域
taillink:出边表指针域
1.有向图十字链表
2.算法实现
四、邻接多重链表
邻接多重链表需要一个头结点保存每个顶点的信息和一个表结点,保存每条边的信息
vertex: 数据域,存储有关顶点的数据信息
firstedge:边表头指针,指向依附于该顶点的边表
ivex、jvex:与某条边依附的两个顶点在顶点表中的下标
ilink:指针域,指向依附于顶点ivex的下一条边
jlink:指针域,指向依附于顶点jvex的下一条边
总结
提示:这里对文章进行总结: