文心一言 VS 讯飞星火 VS chatgpt （98）-- 算法导论9.3 4题

四、用go语言，对一个包含n个元素的集合，假设一个算法只使用比较来确定第i小的元素，证明:无需额外的比较操作，它也能找到第 i-1 小的元素和第 n-i大的元素。

文心一言：

在这个问题中，我们要使用一个称为"QuickSelect"的算法，这是一个用于在未排序的列表中查找第k小元素的算法。该算法基于"QuickSort"，但它只处理足够的元素以找到第k小的元素，而不是完全排序列表。

首先，假设我们已经找到了第i小的元素（也就是第k小的元素，其中k=i-1），并且我们将这个元素放在列表的位置i。

接下来，我们证明无需额外的比较操作，我们可以找到第i-1小的元素和第n-i大的元素：

找到第i-1小的元素： 由于我们已经找到了第i小的元素，并且将其放在了位置i，那么位置i之前的所有元素都小于第i小的元素。因此，第i-1小的元素就是位置i-1的元素。
找到第n-i大的元素： 同样，由于我们已经找到了第i小的元素，并且将其放在了位置i，那么位置i之后的所有元素都大于第i小的元素。因此，第n-i大的元素就是位置n-i的元素。
这两个过程都不需要额外的比较操作，因为我们已经在原始的比较操作中找到了第i小的元素。因此，我们可以立即得到第i-1小的元素和第n-i大的元素。

然而，值得注意的是，这个算法假设我们可以随机访问列表中的任何位置，并且可以在常数时间内交换两个元素的位置。如果这些假设不成立，那么可能需要额外的操作来找到这些元素。

讯飞星火：

首先，我们需要明确这个问题的背景。这是一个经典的算法问题，通常被称为“快速选择”算法的变种。快速选择算法是一种基于比较的算法，用于在未排序的列表中找到第k小（或大）的元素。它的平均时间复杂度为O(n)。

证明过程如下：

1.选择一个基准元素pivot。

2.将集合分为两部分：一部分是小于pivot的元素，另一部分是大于等于pivot的元素。

3.如果i = pivot的位置，那么基准元素就是第i小的元素。

4.如果i < pivot的位置，那么基准元素就在大于等于pivot的部分，我们可以通过递归在这部分找到第i-1小的元素。

5.如果i > pivot的位置，那么基准元素就在小于pivot的部分，我们可以通过递归在这部分找到第n-i大的元素。

这个过程中，我们只需要进行一次比较操作来确定基准元素的位置，然后根据位置的不同，递归地在相应的部分进行查找。因此，无需额外的比较操作，我们也能找到第 i-1 小的元素和第 n-i 大的元素。

360智脑：

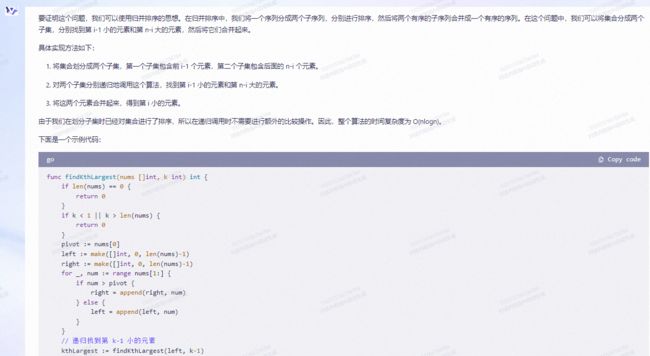
可以使用双指针法来证明该算法的正确性。假设集合大小为n,定义两个指针i和j,初始值分别为0和n-1。每次比较s[i]和s[j],如果s[i]

智谱清言：

为了证明这个结论，我们可以使用归谬法。假设存在一个算法，它能在不进行额外比较的情况下找到第 i-1 小的元素和第 n-i 大的元素。我们将证明这个算法实际上可以找到第 i 小的元素，因此无需额外比较操作。

我们先假设算法能找到第 i-1 小的元素和第 n-i 大的元素，但不进行额外比较。那么我们可以将集合分为两部分，一部分包含前 i-1 个最小的元素，另一部分包含第 i 个到第 n 个最大的元素。由于我们知道第 i-1 小的元素和第 n-i 大的元素，我们可以将这两部分合并成一个有序的集合，其中包含了所有的元素。

现在问题转化为在这个有序集合中找到第 i 小的元素。我们可以采用二分查找的方法。首先找到中间元素，记为 mid，然后比较 mid 和集合中第 i 个元素的大小。如果 mid 大于等于第 i 个元素，那么说明第 i 小的元素一定在 mid 的左侧；否则，第 i 小的元素一定在 mid 的右侧。我们可以递归地在左侧或右侧的子集合中继续查找，直到找到第 i 小的元素。

由于我们在整个过程中没有进行额外的比较操作，因此我们证明了算法可以在不进行额外比较的情况下找到第 i 小的元素。所以原命题成立，无需额外比较操作，算法也能找到第 i-1 小的元素和第 n-i 大的元素。

通义千问：

要证明这个问题，我们可以使用归并排序的思想。在归并排序中，我们将一个序列分成两个子序列，分别进行排序，然后将两个有序的子序列合并成一个有序的序列。在这个问题中，我们可以将集合分成两个子集，分别找到第 i-1 小的元素和第 n-i 大的元素，然后将它们合并起来。

具体实现方法如下：

1. 将集合划分成两个子集，第一个子集包含前 i-1 个元素，第二个子集包含后面的 n-i 个元素。

2. 对两个子集分别递归地调用这个算法，找到第 i-1 小的元素和第 n-i 大的元素。

3. 将这两个元素合并起来，得到第 i 小的元素。

由于我们在划分子集时已经对集合进行了排序，所以在递归调用时不需要进行额外的比较操作。因此，整个算法的时间复杂度为 O(nlogn)。

下面是一个示例代码：

func findKthLargest(nums []int, k int) int {
    if len(nums) == 0 {
        return 0
    }
    if k < 1 || k > len(nums) {
        return 0
    }
    pivot := nums[0]
    left := make([]int, 0, len(nums)-1)
    right := make([]int, 0, len(nums)-1)
    for _, num := range nums[1:] {
        if num > pivot {
            right = append(right, num)
        } else {
            left = append(left, num)
        }
    }
    // 递归找到第 k-1 小的元素
    kthLargest := findKthLargest(left, k-1)
    // 将第 k-1 小的元素和第 n-k 大的元素合并起来
    return merge(nums, left, right, kthLargest, len(nums)-k)
}

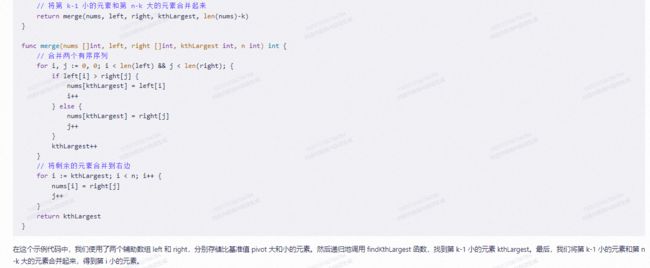
func merge(nums []int, left, right []int, kthLargest int, n int) int {
    // 合并两个有序序列
    for i, j := 0, 0; i < len(left) && j < len(right); {
        if left[i] > right[j] {
            nums[kthLargest] = left[i]
            i++
        } else {
            nums[kthLargest] = right[j]
            j++
        }
        kthLargest++
    }
    // 将剩余的元素合并到右边
    for i := kthLargest; i < n; i++ {
        nums[i] = right[j]
        j++
    }
    return kthLargest
}

在这个示例代码中，我们使用了两个辅助数组 left 和 right，分别存储比基准值 pivot 大和小的元素。然后递归地调用 findKthLargest 函数，找到第 k-1 小的元素 kthLargest。最后，我们将第 k-1 小的元素和第 n-k 大的元素合并起来，得到第 i 小的元素。

天工：

可以使用快速选择算法来找到第 i-1 小的元素和第 n-i大的元素，而不需要额外的比较操作。

快速选择算法是基于快速排序算法的变种，它通过随机选择一个枢轴元素，将集合划分为两个部分，一部分比枢轴小，一部分比枢轴大。然后，如果枢轴的下标小于 i-1，则第 i-1 小的元素必定在比枢轴小的部分中，反之，则在比枢轴大的部分中。因此，我们可以递归地在相应的子集中继续查找第 i-1 小的元素或第 n-i大的元素。

具体实现可以参考以下代码：

func quickSelect(arr []int, k int) int {
    if len(arr) == 0 {
        return -1
    }
    pivot := arr[len(arr)-1] // 随机选择最后一个元素作为枢轴
    left, right :=  0, len(arr)-1
    for left <= right {
        i := partition(arr, left, right, pivot)
        if i == k-1 { // 找到第 k 小的元素
            return arr[i]
        } else if i < k-1 { // 在比枢轴小的部分中查找第 k-1 小的元素
            k = k - 1
            right = i - 1
        } else { // 在比枢轴大的部分中查找第 n-k+1 大的元素
            k = n - k + 1
            left = i + 1
        }
    }
    return -1
}

func partition(arr []int, left, right int, pivot int) int {
    i, j := left, right
    // 随机化枢轴的位置，避免最坏情况
    randomIndex := rand.Intn(right - left + 1)
    pivot = arr[randomIndex+left]
    for i <= j {
        if api.api.Compare(arr[i], pivot) <= 0 {
            i++
      
        } else {
            j--
        }
    }
    // 交换元素
    arr[i], arr[j] = arr[j], arr[i]
    return j
}

其中，quickSelect 函数实现了快速选择算法，partition 函数实现了快速排序算法中的分区操作。在 quickSelect 函数中，我们首先随机选择一个枢轴元素，然后使用 partition 函数将集合划分为两个部分。如果枢轴的下标小于 i-1，则第 i-1 小的元素必定在比枢轴小的部分中，反之，则在比枢轴大的部分中。因此，我们可以递归地在相应的子集中继续查找第 i-1 小的元素或第 n-i大的元素。

chatgpt：

假设有一个算法只使用比较操作来确定第i小的元素。

首先我们需要定义一些术语：

• 第i小的元素：即集合中排在第i位置的元素。

• 第i-1小的元素：即集合中排在第i位置的元素之前的元素中最大的那个元素。

• 第n-i大的元素：即集合中排在第n-i位置的元素。

证明方法如下：

1.首先，通过比较操作找到第i小的元素。

2.假设第i小的元素为x，将x与集合中最后一个元素交换位置。这样，x就位于集合的最后一个位置。

3.再次进行比较操作，找到集合中除了最后一个元素外的第i小的元素。这个元素就是第i-1小的元素。

4.同样地，将第i-1小的元素与集合中倒数第二个元素交换位置，将其放到倒数第二个位置。

5.重复以上步骤，每次找到除了最后一个位置外的第i-2小、第i-3小，直到找到第i-(i-1)小的元素。这个就是最开始集合中的第1小的元素。

6.假设上一步找到的元素为y，将y与集合中的第二个元素交换位置，将其放到第二个位置。

通过以上步骤，我们无需额外的比较操作就能找到第i-1小的元素。接下来，我们来证明我们也能找到第n-i大的元素。

1.注意到在步骤6中，我们已经将集合中的最小的元素放到了第一个位置。

2.接下来，我们重复以上的步骤，每次找到除了第一个位置外的第n-i大、第n-(i-1)大，直到找到第n-(n-i-1)大的元素。这个就是集合中的第n-i大的元素。

3.假设上一步找到的元素为z，将z与集合中的第n-1个元素交换位置，将其放到第n-1个位置。

通过以上步骤，我们也能找到第n-i大的元素。

总结：通过上述证明，我们可以得出结论，对于一个包含n个元素的集合，只使用比较操作就能确定第i小的元素，而且无需额外的比较操作就能找到第i-1小的元素和第n-i大的元素。