灰狼算法Grey Wolf Optimizer跑23个经典测试函数|含源码

智能优化算法（Grey Wolf Optimizer）

---

---

前言

灰狼算法简介：
灰狼优化算法（Grey Wolf Optimization，GWO）是一种基于自然界灰狼行为的启发式优化算法。该算法模仿了灰狼群体中不同等级的灰狼间的优势竞争和合作行为，通过不断搜索最优解来解决复杂的优化问题。

1. 优点：较强的收敛性能，结构简单、需要调节的参数少，容易实现，存在能够自适应调整的收敛因子以及信息反馈机制，能够在局部寻优与全局搜索之间实现平衡，因此在对问题的求解精度和收敛速度方面都有良好的性能。

2. 缺点：存在着易早熟收敛，面对复杂问题时收敛精度不高，收敛速度不够快

---

灰狼算法实现

一、灵感

灰狼属于犬科动物，被认为是顶级的捕食者，它们处于生物圈食物链的顶端。灰狼大多喜欢群居，每个群体中平均有5~12只狼。特别令人感兴趣的一方面是，它们具有非常严格的社会等级制度，如图所示。

$GWO$算法具有结构简单、需要调节的参数少、容易实现等特点，其中存在能够自适应调整的收敛因子以及信息反馈机制，能够在局部寻优与全局搜索之间实现平衡，因此在对问题的求解精度和收敛速度方面都有良好的性能。

金字塔第一层为种群中的领导者，称为 α 。在狼群中 α 是具有管理能力的个体，主要负责关于狩猎、睡觉的时间和地方、食物分配等群体中各项决策的事务。金字塔第二层是 α 的智囊团队，称为 β 。 β 主要负责协助α 进行决策。当整个狼群的 α 出现空缺时，β 将接替 α 的位置。 β 在狼群中的支配权仅次于 α它将 α 的命令下达给其他成员，并将其他成员的执行情况反馈给 α 起着桥梁的作用。金字塔第三层是 δ，δ 听从 α 和 β 的决策命令，主要负责侦查、放哨、看护等事务。适应度不好的 α 和 β 也会降为 δ 。金字塔最底层是 ω ，主要负责种群内部关系的平衡。

---

此外，集体狩猎是灰狼的另一个迷人的社会行为。灰狼的社会等级在群体狩猎过程中发挥着重要的作用，捕食的过程在 α 的带领下完成。灰狼的狩猎包括以下 ３ 个主要部分：
１ ）跟踪、追逐和接近猎物；
２ ）追捕、包围和骚扰猎物，直到它停止移动；
３ ）攻击猎物。

二、GWO数学模型

为了对 ＧＷＯ 中灰狼的社会等级进行数学建模，将前 ３匹最好的狼（最优解）分别定义为 α ，β 和 δ ，它们指导其他狼向着目标搜索。其余的狼（候选解）被定义为 ω ，它们围绕 α ，β或 δ 来更新位置。

1、包围猎物

$$\begin{gathered} \mathcal{D}=\mid C\ast X_P\left(t\right)-X(t)\mid 式（1） \\ vecX(t+1)=X_p(t)-\mathcal{A}\ast D式（2） \end{gathered}$$

$$\begin{gathered} A=2\overrightarrow{a}\ast {\overrightarrow{r}}_1-\overrightarrow{a} \\ C=2\cdot r_2 \end{gathered}$$

---

2、狩猎

灰狼能够识别猎物的位置并包围它们。当灰狼识别出猎物的位置后，β 和 δ 在 α 的带领下指导狼群包围猎物。在优化问题的决策空间中，我们对最佳解决方案（猎物的位置）并不了解。

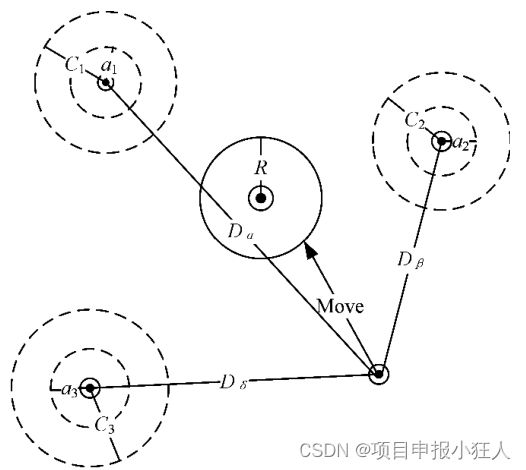
灰狼个体跟踪猎物位置的数学模型描述如下

3、攻击猎物

4、开发

灰狼根据 α ，β 和 δ 的位置来搜索猎物。灰狼在寻找猎物
时彼此分开，然后聚集在一起攻击猎物。基于数学建模的散
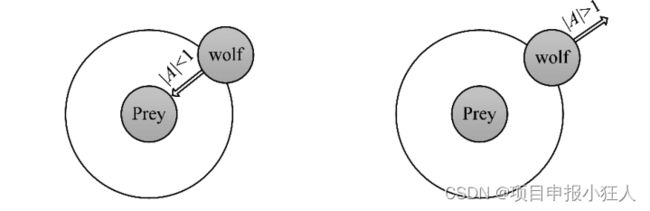
度，可以用 $A$大于 １ 或小于 -1 的随机值来迫使灰狼与猎物分离，这强调了勘探（探索）并允许 ＧＷＯ 算法全局搜索最优解,如图３ （ ｂ ）所示， $\Vert vecA|$＞１强迫灰狼与猎物（局部最优）分离，希望找到更合适的猎物（全局最优）。

5、代码实现

% 灰狼优化算法
function [Alpha_score,Alpha_pos,Convergence_curve]=GWO(SearchAgents_no,Max_iter,lb,ub,dim,fobj)
    % initialize alpha, beta, and delta_pos
    Alpha_pos=zeros(1,dim);
    Alpha_score=inf; %change this to -inf for maximization problems
    
    Beta_pos=zeros(1,dim);
    Beta_score=inf; %change this to -inf for maximization problems
    
    Delta_pos=zeros(1,dim);
    Delta_score=inf; %change this to -inf for maximization problems
    
    %Initialize the positions of search agents
    Positions=initialization(SearchAgents_no,dim,ub,lb);
    
    Convergence_curve=zeros(1,Max_iter);
    
    l=0;% Loop counter
    
    % Main loop
while l<Max_iter
    for i=1:size(Positions,1)  
       % 返回超出搜索空间边界的搜索值
        Flag4ub=Positions(i,:) > ub;
        Flag4lb=Positions(i,:) < lb;
        Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;               
        
        % 计算每个搜索的目标函数值
        fitness=fobj(Positions(i,:));
        
        % 更新位置、Update alpha
        if fitness<Alpha_score 
            Alpha_score=fitness; 
            Alpha_pos=Positions(i,:);
        end
        
        if fitness > Alpha_score && fitness<Beta_score 
            Beta_score=fitness; % Update beta
            Beta_pos=Positions(i,:);
        end
        
        if fitness>Alpha_score && fitness>Beta_score && fitness<Delta_score 
            Delta_score=fitness; % Update delta
            Delta_pos=Positions(i,:);
        end
    end
    
%     a∈[0,2]
    a=2-l*((2)/Max_iter); % a decreases linearly fron 2 to 0
    
    % 更新位置
    for i=1:size(Positions,1)
        for j=1:size(Positions,2)     
              % r1 is a random number in [0,1]         
            r1=rand(); 
             % r2 is a random number in [0,1]
            r2=rand();
            
            A1=2*a*r1-a; % Equation (3.3)
            C1=2*r2; % Equation (3.4)
            
            D_alpha=abs(C1*Alpha_pos(j)-Positions(i,j)); % Equation (3.5)-part 1
            X1=Alpha_pos(j)-A1*D_alpha; % Equation (3.6)-part 1
                       
            r1=rand();
            r2=rand();
            
            A2=2*a*r1-a; % Equation (3.3)
            C2=2*r2; % Equation (3.4)
            
            D_beta=abs(C2*Beta_pos(j)-Positions(i,j)); % Equation (3.5)-part 2
            X2=Beta_pos(j)-A2*D_beta; % Equation (3.6)-part 2       
            
            r1=rand();
            r2=rand(); 
            
            A3=2*a*r1-a; % Equation (3.3)
            C3=2*r2; % Equation (3.4)
            
            D_delta=abs(C3*Delta_pos(j)-Positions(i,j)); % Equation (3.5)-part 3
            X3=Delta_pos(j)-A3*D_delta; % Equation (3.5)-part 3             
            
            Positions(i,j)=(X1+X2+X3)/3;% Equation (3.7)
            
        end
    end
    l=l+1;    
    Convergence_curve(l)=Alpha_score;
end




%%函数声明，输入参数包括搜索代理数量（SearchAgents_no）、问题维度（dim）、上界（ub）和下界（lb）。输出为搜索代理的位置矩阵
function Positions=initialization(SearchAgents_no,dim,ub,lb)
% 获取上界矩阵的列数，即边界数量，判断变量边界的情况
    Boundary_no= size(ub,2); % numnber of boundaries
    
    % If the boundaries of all variables are equal and user enter a signle
    % number for both ub and lb
    if Boundary_no==1
        Positions=rand(SearchAgents_no,dim).*(ub-lb)+lb;
    end
    
    % If each variable has a different lb and ub
    if Boundary_no>1
        for i=1:dim
            ub_i=ub(i);
            lb_i=lb(i);
            Positions(:,i)=rand(SearchAgents_no,1).*(ub_i-lb_i)+lb_i;
        end
    end

总结

完整代码请私信领取：

[1].Mirjalili, S., Mirjalili, S. M., & Lewis, A. (2014). Grey wolf optimizer. Advances in engineering software, 69, 46-61.