一种数字全息散斑干涉测量仿真模拟系统

一、引言

数字散斑干涉技术是根据激光散斑场会随着被测物体表面变形而变化来获取位移信息的，利用图像处理技术对物体变形前后的散斑场作处理，得到散斑场在物体变形前后的相位变化信息，再根据相位变化与物体变形的关系，得到物体变形信息。

利用任何一种散斑干涉测量系统测量微小形变，直接采集到的都是加载前后的散斑干涉图，所以要继续对这对散斑干涉图像做相应处理，才能得到含有待测物形变信息的散斑条纹图。

本博文主要将对散斑干涉条纹图获取进行仿真模拟分析，探究散斑尺寸大小影响因素，分析五步相移算法的原理，并将其用于相位信息的提取。

二、数字散斑干涉原理分析

2.1 散斑尺寸大小控制

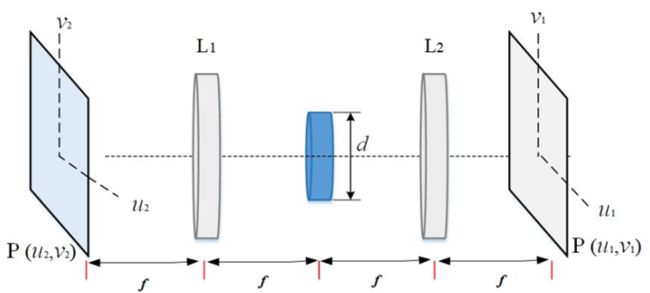
待测件表面一般粗糙且复杂多变，若激光照射在表面上会发生散射现象，且散射光相互干涉产生明暗相间的散斑。为了生成散斑图，采用模仿4f系统操纵光场光谱的方式来模拟散斑图。图1所示的光场中，透镜L1和透镜L2具有相等的焦距f。考虑到激光照射在被测元件的表面是粗糙的，因此可视为随机相位。在透镜L1后的焦平面(傅立叶平面)增加一直径为d的孔径光阑，而像平面是成像物镜的傅里叶变换。将低通滤波器 作为孔径应用于模拟成像透镜，以产生物光束，数学表达为[1]

$$U_0(u,v)=F^{-1}\left\{d\left(k_1,k_2\right)\times F\left\{a_0\left(u,v\right)\exp \left[i{\phi }_0\left(u,v\right)\right]\right\}\right\}\text{\hspace{1em}(1)}$$

式中，(u,v)为空间坐标；$U_0(u,v)$为物光束；F和$F^{-1}$分别为傅里叶变换和反变换；$a_0\left(u,v\right)$和${\phi }_0\left(u,v\right)$分别代为物光波的幅值和相位，${\phi }_0\left(u,v\right)$作为随机变量均匀分布在$\left(-\pi ,\pi \right]$。

若参考光束记为$U_R(u,v)$，未变形强度图表示为

$$I(u,v)={\left|U_0(u,v)+U_R(u,v)\right|}^2\text{\hspace{1em}(2)}$$

当物体发生形变后，式(1)中物光束的相位项由${\phi }_0\left(u,v\right)$变为${\phi }_0\left(u,v\right)+\Delta \varphi \left(u,v\right)$，变形后的强度也可由式(2)模拟。最后，根据“1+1”算法，将变形前后的强度图相减并取绝对值则可得到散斑条纹图。

图1 散斑图生成过程示意图

2.2 基于五步相移算法的包裹相位提取理论

在参考光路中若推动PZT产生光程差，待测对象在变形前和变形后的5幅相移条纹图数学表示为

$$I_{bi}(u,v)=a(u,v)+b(u,v)\cos \left[\varphi (u,v)+{\delta }_i\right],i=1,2,3,4,5\text{\hspace{1em}(3)}$$

$$I_{ai}(u,v)=a(u,v)+b(u,v)\cos \left[\varphi (u,v)+\Delta \phi \left(u,v\right)+{\delta }_i\right],i=1,2,3,4,5\text{\hspace{1em}(4)}$$

式中，$I_{bi}(u,v)$为未变形条纹图；$I_{ai}(u,v)$为变形条纹图；$a(u,v)$和$b(u,v)$分别为背景光强和对比度；$\varphi (u,v)$为随机散斑相位；${\delta }_i$为相移量；$\Delta \phi \left(u,v\right)$为相位变化量。

式(3)和(4)中，变形前和变形后的条纹图相移间隔${\delta }_i$为$\pi /2$时，相移算法提取的随机散斑相位和变形后散斑相位为

$$\varphi (u,v)=\arctan \left[\frac{2(I_{b2}-I_{b4})}{2I_{b3}-I_{b1}-I_{b5}}\right]\text{\hspace{1em}(5)}$$

$$\varphi (u,v)+\Delta \phi \left(u,v\right)=\arctan \left[\frac{2(I_{a2}-I_{a4})}{2I_{a3}-I_{a1}-I_{a5}}\right]\text{\hspace{1em}(6)}$$

由式(6)减去(5)，即可计算相位变化量$\Delta \phi \left(u,v\right)$。

三、散斑干涉仿真模拟结果

3.1 散斑条纹图中散斑尺寸控制仿真结果

通过调整孔径的方式，可控制散斑的大小。以数值模拟为例，图2展示了不同孔径$d\left(k_1,k_2\right)$大小的散斑条纹，其尺寸为1024×1024像素，结果表明孔径越小则产生的散斑尺寸越大。

图2 不同孔径d的散斑干涉条纹图

3.2 基于五步相移算法的包裹相位信息提取实例

根据五步相移理论，即可进一步获取包裹相位，如下图所示，是采用正余弦滤波算法滤波之后的包裹相位，结果表明，当散斑尺寸越大，进行滤波时会使得包裹相位的细节部分丢失，进而会造成相位重构重构遇到困难。

图3 不同孔径下的变形包裹相位

3.3 相位解包裹

将图3(a)中的包裹相位进行解包裹，结果如下图所示。

图4 相位解包裹信息

参考文献

[1] Ketao Yan, Lin Chang, Michalis Andrianakis, et al. Deep Learning-Based Wrapped Phase Denoising Method for Application in Digital Holographic Speckle Pattern Interferometry [J]. Appl Sci, 2020, 10(11).

---

⭐️◎⭐️◎⭐️◎⭐️ · · · **博 主 简 介** · · · ⭐️◎⭐️◎⭐️◎⭐️ ♪

▁▂▃▅▆▇ 博士研究生生 ，研究方向主要涉及定量相位成像领域，具体包括干涉相位成像技术(如**全息干涉☑**、散斑干涉☑等)、非干涉法相位成像技术(如波前传感技术☑，相位恢复技术☑)、此外，还对各种相位解包裹算法☑，相干噪声去除算法☑等开展过深入的研究。

---