二进制基础及位运算

一、什么是二进制

二进制是计算机运算时所采用的数制，基数是2，也就是说它只有两个数字符号，即0和1。如果在给定的数中，除0和1外还有其他数（例如1061），那它就绝不会是一个二进制数了。二进制数的最大数码也是基数减1，即2-1=1，最小数码也是0。二进制数的标志为B，如（1001010）B，也可用下标“2”来表示，如（1001010）2（注意是下标）。

二、二进制转换为十进制

二进制转换成十进制的方法，大家可能早就有所了解了，如在IPv4地址计算时就经常进行这样的操作。转换的方法比较简单，只需按它的权值展开即可。展开的方式是把二进制数首先写成加权系数展格式，然后按十进制加法规则求和。这种方法称为“按权相加”法。

二进制整数部分的一般表现形式为：bn-1…b1b0（共n位），按权相加展开后的格式为（注意，展开式中从左往右各项的幂次是从高到低下降的，最高位的幂为n-1，最低的幂为0）：

如二进制数（11010）2的按权相加展开格式为：

用一句话概括来说就是:二进制数*基数的索引次幂相加之和

二进制小数部分的幂次是反序排列的（也就是与整数部分的幂次序列相反，从左往右其绝对值是从低到高上升的），且为负值，最高位幂次（也就是最靠近小数点的第一个小数位的幂次）为“-1”。如二进制小数部分的格式为：0.bn-1…b1b0，则按权相加后的展开格式为：

如（0.1011）2的按权相加展开格式为：

三、十进制转二进制

十进制整数转换为二进制的方法是：采用“除2逆序取余”法（采用短除法进行）。也就是先将十进制数除以2，得到一个商数（也是下一步的被除数）和余数；然后再将商数除以2，又得到一个商数和余数；以此类推，直到商数为小于2的数为止。然后从最后一步得到的小于2的商数开始将其他各步所得的余数（也都是小于2的0或1）排列起来（俗称“逆序排列”）就得到了对应的二进制数。

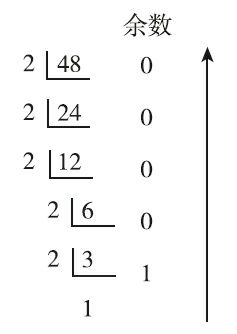
图　1-1　十进制整数48转换成二进制整数的步骤

图　1-2　十进制整数250转换成二进制整数的步骤

简便算法：记住2的10次幂1024内的次幂值，比如计算114的二进制

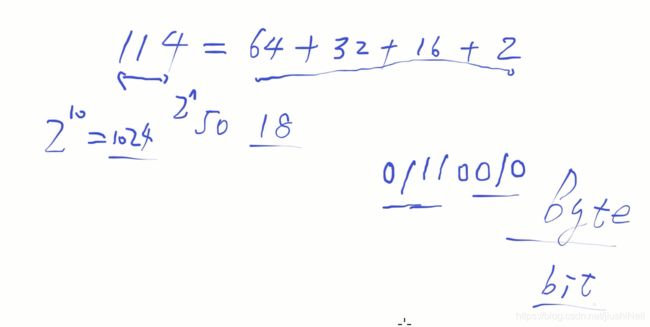
四、二进制逻辑运算

在计算机中所有数据都是以二进制的形式储存的。位运算其实就是直接对在内存中的二进制数据进行操作，因此处理数据的速度非常快。
在实际编程中，如果能巧妙运用位操作，完全可以达到四两拨千斤的效果，正因为位操作的这些优点，所以位操作在各大IT公司的笔试面试中一直是个热点问题。因此本文将对位操作进行如下方面总结：

• 位操作基础，用一张表描述位操作符的应用规则并详细解释。
• 常用位操作小技巧，判断奇偶、交换两数、变换符号、求绝对值。
• 位操作与空间压缩，针对筛素数进行空间压缩。

1、位操作基础

基本的位操作符有与、或、异或、取反、左移、右移、无符号右移这7种，它们的运算规则如下所示：

符号	描述	运算规则
&	与	遇0则0
|	或	遇1则1
~	非	求反，1变0，0变1
^	异或	不进位加(相同为0，相异为1)
>>	右移	左补符号位
<<	左移	右补0
>>>	无符号右移	左补0

注:
1、在这6种操作符，只有~取反是单目操作符，其它5种都是双目操作符。
2、位操作只能用于整形数据，对float和double类型进行位操作会被编译器报错。
3、位操作符的运算优先级比较低，因此尽量使用括号来确保运算顺序，否则很可能会得到莫明其妙的结果。比如要得到像1，3，5，9这些2^i+1的数字。写成int a = 1 << i + 1;是不对的，程序会先执行i + 1，再执行左移操作。应该写成int a = (1 << i) + 1;
4、另外位操作还有一些复合操作符，如&=、|=、 ^=、<<=、>>=。

2、常用位操作小技巧

下面对位操作的一些常见应用作个总结，有判断奇偶、交换两数、变换符号及求绝对值。这些小技巧应用易记，应当熟练掌握。

1.判断奇偶

只要根据最末位是0还是1来决定，为0就是偶数，为1就是奇数。因此可以用
if ((a & 1) == 0 )代替if (a % 2 == 0)来判断a是不是偶数。
下面程序将输出0到100之间的所有奇数。

    static void oddOrEven() {
        IntStream.rangeClosed(1, 100)
                .filter((i) -> (i & 1) == 1)
                .forEach(System.out::println);
    }

2.交换两数

一般的写法是：

static void swap(int a, int b) {
	//定义一个临时变量
	int c = a;
	a = b;
	b = c;
}

static void swap(int a, int b) {
        a = a^b;
        b = a^b;
        a = a^b;
        System.out.println("a=" + a + ",b= " + b);
    }

可以这样理解：
第一步：a = a^b
第二部：b = a^b = （a^b）^b=第一步的值^b。由于运算满足交换律，(a^b)^b=a^b^b。由于一个数和自己异或的结果为0并且任何数与0异或都会不变的，所以此时b被赋上了a的值。
第三步 a=a^b，由于前面二步可知a=(a^b)，b=a，所以a=a^b即a=(a^b)^a。故a会被赋上b的值。

再来个实例说明下以加深印象。int a = 13, b = 6;
a的二进制为 13=8+4+1=1101(二进制)
b的二进制为 6=4+2=0110(二进制)
第一步 a=a^b a = 1101 ^ 0110 = 1011;
第二步 b=a^b b = 1011 ^ 0110 = 1101;即b=13
第三步 a=a^b a = 1011 ^ 1101 = 0110;即a=6

3.变换符号

变换符号就是正数变成负数，负数变成正数。
如对于-11和11，可以通过下面的变换方法将-11变成11
1111 0101(二进制) –取反-> 0000 1010(二进制) –加1-> 0000 1011(二进制)
同样可以这样的将11变成-11
0000 1011(二进制) –取反-> 1111 0100(二进制) –加1-> 1111 0101(二进制)
因此变换符号只需要取反后加1即可。完整代码如下：

	static void signReversal(int a) {
        a = ~a + 1;
        System.out.println(a);
    }

4.求绝对值

位操作也可以用来求绝对值，对于负数可以通过对其取反后加1来得到正数。对-6可以这样：
1111 1010(二进制) –取反->0000 0101(二进制) -加1-> 0000 0110(二进制)
来得到6。
因此先移位来取符号位，int i = a >> 31;要注意如果a为正数，i等于0，为负数，i等于-1。然后对i进行判断——如果i等于0，直接返回。否之，返回~a+1。完整代码如下：

	static void abs(int a) {
        a = (a >> 31) == 0 ? a : ~a + 1;
        System.out.println(a);
    }

现在再分析下。对于任何数，与0异或都会保持不变，与-1即0xFFFFFFFF异或就相当于取反。因此，a与i异或后再减i（因为i为0或-1，所以减i即是要么加0要么加1）也可以得到绝对值。所以可以对上面代码优化下：

    static void absNoDecide(int a) {
        int i = a >> 31;
        a = (a ^ i) - i;
        System.out.println(a);
    }

注意这种方法没用任何判断表达式，因此建议读者记住该方法（^_^讲解过后应该是比较好记了）。

5、获得int最大值

System.out.println((1 << 31) - 1);// 2147483647， 由于优先级关系，括号不可省略
System.out.println(~(1 << 31));// 2147483647

6、获得int型最小值

System.out.println(1 << 31);
System.out.println(1 << -1);

7、获得long类型的最大值

System.out.println(((long)1 << 127) - 1);

8、乘以2运算

System.out.println(n << 1);

9、除以2运算(负奇数的运算不可用，精度缺失)

System.out.println(n >> 1);

10、m乘以2的n次方

System.out.println(m << n);

11、m除以2的n次方

System.out.println(m >> n);

12、取两个数的最大值（某些机器上，效率比a>b ? a:b高）

System.out.println(b & ((a - b) >> 31) | a & (~(a - b) >> 31));

13、取两个数的最小值（某些机器上，效率比a>b ? b:a高）

System.out.println(a & ((a - b) >> 31) | b & (~(a - b) >> 31));

14、判断符号是否相同(true 表示 x和y有相同的符号， false表示x，y有相反的符号。)

System.out.println((a ^ b) > 0);

15、计算2的n次方 n > 0

System.out.println(2 << (n - 1));

16、判断一个数n是不是2的幂

/*如果是2的幂，n一定是100... n-1就是1111....所以做与运算结果为0*/
System.out.println((n & (n - 1)) == 0);

17、求两个整数的平均值

System.out.println((a + b) >> 1);

18、从低位到高位,取n的第m位

int m = 2;
System.out.println((n >> (m - 1)) & 1);

19、从低位到高位.将n的第m位置为1

/*将1左移m-1位找到第m位，得到000...1...000 n在和这个数做或运算*/
System.out.println(n | (1<<(m-1)));

20、从低位到高位,将n的第m位置为0

/* 将1左移m-1位找到第m位，取反后变成111...0...1111 n再和这个数做与运算*/
System.out.println(n & ~(0 << (m - 1)));

常见操作技巧

取高位右移，取低位相与

3、位操作与空间压缩

筛素数法在这里不就详细介绍了，本文着重对筛素数法所使用的素数表进行优化来减小其空间占用。要压缩素数表的空间占用，可以使用位操作。下面是用筛素数法计算100以内的素数示例代码（注2）：

	static void getPrime() {
        int max = 100;
        boolean[] flag = new boolean[100];
        int[] primes = new int[max / 3 + 1];

        int i, j;
        int pi = 0;
        for (i = 2; i < max; i++) {
            if (!flag[i]) {
                primes[pi++] = i;
                /**
                 * 对于每个素数，它的倍数必定不是素数
                 */
                for (j = i; j < max; j += i)
                    flag[j] = true;
            }
        }

        Arrays.stream(primes)
                .limit(pi)
                .forEach((p) -> System.out.print(p + ","));
    }

在上面程序是用boolean数组来作标记的，boolean型数据占1个字节（8位），因此用位操作来压缩下空间占用将会使空间的占用减少八分之七。
下面考虑下如何在数组中对指定位置置1，先考虑如何对一个整数在指定位置上置1。对于一个整数可以通过将1向左移位后与其相或来达到在指定位上置1的效果，代码如下所示：

//在一个数指定位置上置1
int i = 0;
i |= i << 10;

同样，可以1向左移位后与原数相与来判断指定位上是0还是1（也可以将原数右移若干位再与1相与）。

//判断指定位上是0还是1
int i = 1 << 10;
if ((i & (1 << 10)) != 0) {
	System.out.println("指定位上为1");
} else {
	System.out.println("指定位上为0");
}

扩展到数组上，我们可以采用这种方法，因为数组在内存上也是连续分配的一段空间，完全可以“认为”是一个很长的整数。先写一份测试代码，看看如何在数组中使用位操作：

		int[] bits = new int[40];

        for (int m = 0; m < 40; m += 3) {
            bits[m / 32] |= (1 << (m % 32));
        }

        // 输出整个bits
        for (int m = 0; m < 40; m++) {
            if (((bits[m / 32] >> (m % 32)) & 1) != 0) {
                System.out.print('1');
            } else {
                System.out.print('0');
            }
        }

运行结果如下：
1001001001001001001001001001001001001001

可以看出该数组每3个就置成了1，证明我们上面对数组进行位操作的方法是正确的。因此可以将上面筛素数方法改成使用位操作压缩后的筛素数方法：

	static void getPrimeByBitwise() {
        int max = 100;
        int[] flag = new int[max/32 + 1];
        int[] primes = new int[max / 3 + 1];

        int i, j;
        int pi = 0;
        for (i = 2; i < max; i++) {
            if ((((flag[i/32] >> (i % 32))& 1) == 0)) {
                primes[pi++] = i;
                /**
                 * 对于每个素数，它的倍数必定不是素数
                 */
                for (j = i; j < max; j += i)
                    flag[j/32] |= (1 << (j % 32));
            }
        }

        Arrays.stream(primes)
                .limit(pi)
                .forEach((p) -> System.out.print(p + ","));
    }