C++容器篇,stack和queue
C++容器篇——stack和queue
1 stack的介绍和使用
1.1 stack的介绍
stack的参考文档
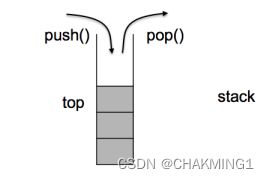
stack是一种容器适配器,其本质是数据结构中的栈。它是一种只能在一端进行插入和删除操作的线性表。
stack的底层是用容器适配器来实现的,容器适配器是对特定类封装作为其底层的容器,并提供一组接口来访问其元素,那么,它的底层容器应该要支持栈的基本操作。
- empty:判空操作。
- back:获取尾部元素的操作,这是因为栈的top操作相当于拿取尾部元素。
- push_back:尾部插入元素操作。
- pop_back:尾部删除元素操作。
那么,标准容器下的vector、deque、list均符合这些需求,默认情况下使用deque(本章会介绍)。
1.2 stack的使用
stack必须包含头文件#include ,并且属于std命名空间里面。
#include 这是一个简单的使用stack的案例,首先先创建一个stack容器,push()将数据压入栈中,stack并不支持迭代器访问,我们通过接口empty()判断栈是否为空,通过top()访问栈顶元素,pop()将数据出栈。
1.2.1 stack的定义
stack是一个容器适配器,所以通常在创建时,采用的都是无参构造,但是可以在模板参数内传入底层所使用的容器,例如:
int main()
{
stack<int> st; // 默认使用deque作为底层容器
stack<int, vector<int>> st2; // 使用vector作为底层容器
}
1.2.2 stack的方法介绍
| 函数说明 | 接口说明 |
|---|---|
| empty | 检测stack是否为空 |
| size | 返回stack的元素个数 |
| top | 返回栈顶元素的引用 |
| push | 将元素压入栈中 |
| pop | 将顶部的元素出栈。 |
1.3 栈的应用
155.最小栈
设计一个支持 push ,pop ,top 操作,并能在常数时间内检索到最小元素的栈。
思想介绍:设计两个栈,一个负责保存栈的元素,一个负责保存栈的最小值。只要有元素比最小值栈的顶部元素还有小,那么,就将这个值压入最小值栈中,这样就能保证,最小值栈的顶部元素永远是当前压入的所有元素中最小的。
class MinStack {
public:
MinStack() {
}
void push(int val) {
st.push(val);
if(minst.empty() || val <= minst.top())
{
minst.push(val);
}
}
void pop() {
if(minst.top() == st.top())
{
minst.pop();
}
st.pop();
}
int top() {
return st.top();
}
int getMin() {
return minst.top();
}
private:
stack<int> st;
stack<int> minst; // 辅助栈
};
JZ31 栈的压入、弹出序列
输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。
思想介绍:借助一个辅助栈,首先,创建两个变量i和j,分别指向pushV数组的元素和popV数组的元素,然后将pushV的数据压入栈中,直到遇到顶部元素恰好等于出栈序列的元素,那么就将栈顶元素出栈,并且j++。最后,如果栈的元素不为空,那么说明当前出栈序列不符合。
class Solution {
public:
bool IsPopOrder(vector<int> pushV,vector<int> popV) {
stack<int> st;
int i = 0, j = 0;
for(; i < pushV.size();++i)
{
st.push(pushV[i]);
while(!st.empty() && st.top() == popV[j])
{
st.pop();
j++;
}
}
return st.empty();
}
};
150. 逆波兰表达式求值
给你一个字符串数组 tokens ,表示一个根据 逆波兰表示法 表示的算术表达式。
请你计算该表达式。返回一个表示表达式值的整数。
思想介绍:同样借助一个辅助栈来完成,遍历数组tokens,遇到数值就压入栈中,遇到符号,就弹出两个元素,并且根据符号进行求值。最后,栈顶元素就是最终的表达式结果。
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for(int i = 0;i<tokens.size();++i)
{
if(tokens[i] == "+" || tokens[i] == "-" || tokens[i] == "*" || tokens[i] == "/")
{
int num1 = st.top();
st.pop();
int num2 = st.top();
st.pop();
if(tokens[i] == "+") st.push(num2 + num1);
else if(tokens[i] == "-") st.push(num2 - num1);
else if(tokens[i] == "*") st.push(num2 * num1);
else if(tokens[i] == "/") st.push(num2 / num1);
}
else
{
st.push(stoi(tokens[i])); // stoi 把字符串转为数字
}
}
int result = st.top();
st.pop();
return result;
}
};
232. 用栈实现队列
请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty)。
思想介绍:设计两个栈,一个栈用来入数据,一个栈用来出数据。入队列操作,可以直接将数据插入到stIn中,出队列的时候,如果stOut为空,就将stIn的数据放到stOut中,我们直到栈的特性是后进先出,队列的特性是先进先出,那么将元素放到一个栈中,再出栈到另一个栈中,相当于元素原本的顺序不变,恰好符合队列的要求。
class MyQueue {
public:
stack<int> stIn;
stack<int> stOut;
MyQueue() {
}
void push(int x) {
stIn.push(x);
}
int pop() {
if(stOut.empty())
{
while(!stIn.empty())
{
stOut.push(stIn.top());
stIn.pop();
}
}
int result = stOut.top();
stOut.pop();
return result;
}
// 获取头部元素
int peek() {
int res = this->pop();
stOut.push(res);
return res;
}
bool empty() {
return stIn.empty() && stOut.empty();
}
};
2 stack模拟实现
stack模拟实现的代码非常简单,我们采用vector来实现,底层默认是deque。
#include 3 queue的介绍和使用
3.1 queue的介绍
queue的参考文档
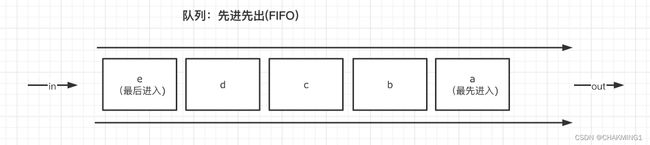
queue是一种容器适配器,专门用于在先进先出上下文中操作,在容器的一端插入元素,另一端删除元素。
queue的底层也是用作容器来进行封装,底层容器必须支持以下操作:
- empty:检测队列是否为空。
- size:返回队列的有效元素个数
- front:返回队头元素的引用
- back:返回队尾元素的引用
- push_back:在队列尾部入队列
- pop_front:在队列头部出队列
标准容器中的deque、list满足了这些要求,默认情况下,使用deque作为底层容器类。
3.2 队列的使用
queue必须包含头文件#include ,并且属于std命名空间里面。
#include 这是一个简单的使用queue的案例,首先先创建一个queue容器,push()将数据入队列中,queue同样并不支持迭代器访问,我们通过接口empty()判断队列是否为空,通过front()访问队列的第一个元素,pop()将数据出队。
3.2.1 queue的定义
queue是一个容器适配器,所以通常在创建时,采用的都是无参构造,但是可以在模板参数内传入底层所使用的容器,例如:
int main()
{
queue<int> q; // 默认使用deque作为底层容器
queue<int, vector<int>> q2; // 使用vector作为底层容器
}
3.2.2 queue的方法介绍
| 函数说明 | 接口说明 |
|---|---|
| empty | 检测queue是否为空 |
| size | 返回queue的元素个数 |
| front | 返回队头元素的引用 |
| back | 返回队尾元素的引用 |
| push | 在队尾将元素入队列 |
| pop | 将队头元素出队列 |
3.3 队列的应用
255.用队列实现栈
请你仅使用两个队列实现一个后入先出(LIFO)的栈,并支持普通栈的全部四种操作(push、top、pop 和 empty)。
思路介绍:使用两个队列,重点在于出栈操作,出栈操作,将队列1的元素,放到队列2,队列1的元素只剩下1个,然后这个作为出栈的元素,之后q1 = q2,然后将q2的元素进行出队。
class MyStack {
public:
queue<int> q1;
queue<int> q2;
MyStack() {
}
void push(int x) {
q1.push(x);
}
int pop() {
int size = q1.size();
size--;
while(size--)
{
q2.push(q1.front());
q1.pop();
}
int result = q1.front();
q1.pop();
q1 = q2;
while(!q2.empty())
{
q2.pop();
}
return result;
}
int top() {
return q1.back();
}
bool empty() {
return q1.empty();
}
};
4 queue模拟实现
因为,queue接口存在头删,使用vector封装效率很低,可以使用list进行模拟实现queue。
#include
namespace ming
{
template<class T>
class queue
{
public:
queue() {}
void push(const T& x) { _c.push_back(x); }
void pop() { _c.pop_front(); }
T& back() { return _c.back(); }
const T& back() const { return _c.back(); }
T& front() { return _c.front(); }
const T& front() const { return _c.front(); }
size_t size() const { return _c.size(); }
bool empty() const { return _c.empty(); }
private:
std::list<T> _c;
};
}
5 priority_queue的介绍和使用
5.1 priority_queue的介绍
priority_queue的参考文档
优先级队列是一种容器适配器,根据严格的弱排序标准,它的第一个元素是所有元素中最大的。
优先级队列的底层是用堆进行实现的,大根堆的堆顶是最大的。
优先级队列的底层容器可以使任何标准容器类模板,也可以是其他特定设计的容器类。容器应该可以通过随机访问迭代器访问,并支持以下操作:
- empty():检测容器是否为空。
- size():返回容器有效元素个数。
- front():返回容器第一个元素的引用
- push_back():在容器尾部插入元素
- pop_back():删除容器尾部元素
标准容器vector和queue都满足以上要求,如果没有特定要求,默认使用vector作为底层容器类。
需要支持随机访问迭代器,保证内部始终保持堆结构。容器适配器在需要的时候调用算法函数make_heap、push_heap和pop_heap来自动完成此操作。
5.2 priority_queue的使用
priority_queue必须包含头文件#include ,并且属于std命名空间里面。
#include 优先级队列默认使用了vector作为底层数据的容器,在vector的基础上又使用堆算法将vector的元素构造成堆,我们知道堆有两种,分别是大根堆和小根堆,默认情况下,是大根堆,如果想要使用小根堆,就要修改比较函数,那么这时候,将greater当作第三个模板参数进行传入。
5.3 优先队列的应用
215. 数组中的第K个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
思路介绍:将数据全部放入到优先级队列中,然后弹出k次元素之后,栈顶就是第k个最大的元素。
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int> pq(nums.begin(),nums.end());
while(--k)
{
pq.pop();
}
return pq.top();
}
};
6 priority_queue的模拟实现
#include 7 容器适配器
7.1 什么是适配器
适配器是一种设计模式,假设已经有一个设计系统,你需要把新的厂商类整合进去,但是,新的厂商类的接口和原来的接口不一致,但是,又不可以修改原有的代码,这个时候,就可以设计一个适配器作为中间人,实现所期望的接口,与新的厂商类进行对接。
7.2 STL标准库中stack和queue的底层结构
stack和queue是对标准库的其他容器的接口进行了包装,STL的stack和queue默认使用deque。
7.3 deque的简单介绍
deque(双端队列):是一种双开口的"连续"空间的数据结构,双开口的含义是:可以在头尾两端进行插入和
删除操作,且时间复杂度为O(1),与vector比较,头插效率高,不需要搬移元素;与list比较,空间利用率比
较高。