2023.9.10 学习周报

目录

摘要

ABSTRACT

一、文献阅读

1、题目

2、ABSTRACT

3、网络结构

1、传统LSTM神经元的内部结构

2、BiLSTM单元的内部结构

3、VMD-BiLSTM实验流程图

4、文章解读

1、Introduction

2、Related model

3、discussion

4、Evaluation metric

5、Experimental process and results

6、Conclusion

二、用pytorch 实现线性回归

 一、numpy中的自动广播机制

二、举例

三、完整代码展示

详细过程

代码

总结

---

摘要

本周读了一篇关于PM2.5的预测的文献，文献中把VMD-BiLSTM与其它现有模型进行比较，VMD-BiLSTM的各方面性能都优于其它模型，VMD根据频域将原始PM2.5复时间序列数据分解为多个子信号分量。然后，采用BiLSTM分别对每个子信号分量进行预测，显著提高了预测精度。

ABSTRACT

This week, I read a paper on the prediction of PM2.5. The paper compared VMD-BiLSTM with other existing models, and found that VMD-BiLSTM outperformed the other models in various aspects. VMD decomposes the original PM2.5 time series data into multiple sub-signal components based on the frequency domain. Then, BiLSTM is used to predict each sub-signal component separately, resulting in a significant improvement in prediction accuracy.

一、文献阅读

1、题目

A hybrid deep learning technology for PM2.5 air quality forecasting

2、ABSTRACT

The concentration ofPM2.5 is one ofthe main factors in evaluating the air quality in environmental science. The severe level of PM2.5 directly affects the public health, economics and social development. Due to the strong nonlinearity and instability ofthe air quality, it is difficult to predict the volatile changes of PM2.5 over time. In this paper, a hybrid deep learning model VMD-
BiLSTM is constructed, which combines variational mode decomposition (VMD) and bidirectional long short-term memory network (BiLSTM), to predict PM2.5 changes in cities in China. VMD decomposes the original PM2.5 complex time series data into multiple sub-signal components according to the frequency domain. Then, BiLSTM is employed to predict each sub-signal
component separately, which significantly improved forecasting accuracy. Through a comprehensive study with existing models,such as the EMD-based models and other VMD-based models, we justify the outperformance of the proposed VMD-BiLSTM model over all compared models. The results show that the prediction results are significantly improved with the proposed forecasting framework. And the prediction models integrating VMD are better than those integrating EMD. Among all the models integrating VMD, the proposed VMD-BiLSTM model is the most stable forecasting method.

PM2.5浓度是环境科学中评价空气质量的主要指标之一。PM2.5的严重程度直接影响到公众健康、经济和社会发展。由于空气质量具有很强的非线性和不稳定性，很难预测PM2.5随时间的波动变化.本文构建了一个结合变分模式分解（VMD）和双向长短期记忆网络（BiLSTM）的混合深度学习模型VMDBiLSTM，用于预测中国城市PM2.5的变化。VMD根据频域将原始PM2.5复时间序列数据分解为多个子信号分量。然后，采用BiLSTM分别对每个子信号分量进行预测，显著提高了预测精度。通过对现有模型（如基于EMD的模型和其他基于VMD的模型）的全面研究，我们证明了所提出的VMD-BiLSTM模型优于所有比较模型。结果表明，所提出的预测框架能显著提高预测结果。集成VMD的预测模型优于集成EMD的预测模型。在所有集成VMD的模型中，所提出的VMD-BiLSTM模型是最稳定的预测方法。

3、网络结构

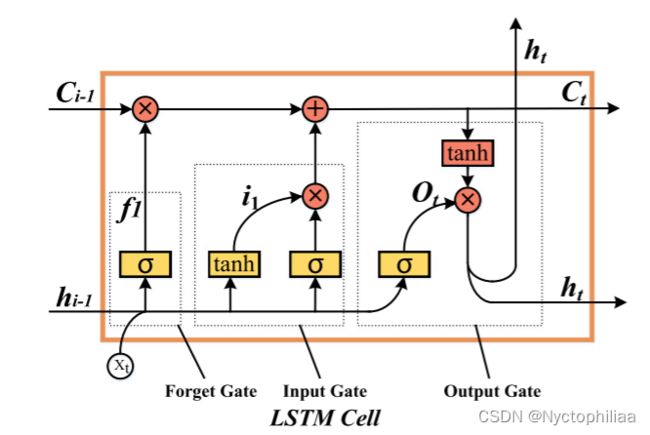
1、传统LSTM神经元的内部结构

在LSTM单元中，起决定性作用的是遗忘门，它选择性地忽略历史信息。第二个是输入门和输出门，用于输入和输出电流单位。

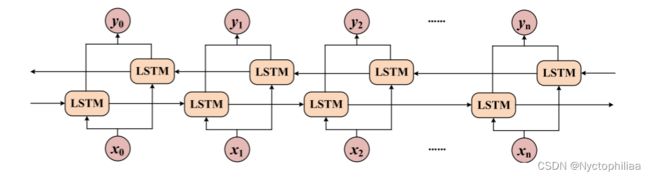
2、BiLSTM单元的内部结构

从图中可以看出，BiLSTM模型由前向LSTM和后向LSTM组成。这使得它分别获得当前时间的前向和后向特性。

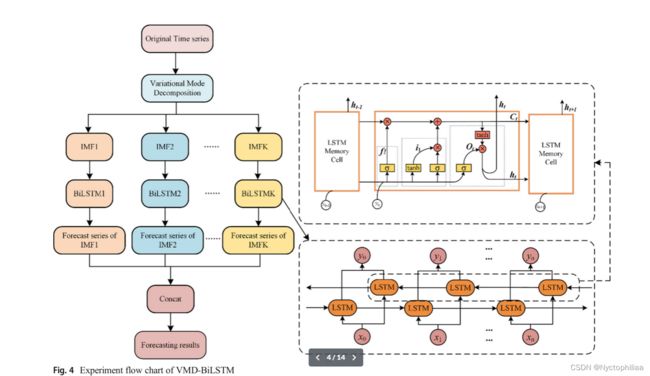
3、VMD-BiLSTM实验流程图

在第一阶段，对原始数据进行标准化和划分。在第二阶段，将单变量PM2.5数据分解为K个IMF，然后应用BiLSTM模型来学习和预测分解的数据分量。在最后一个阶段，BiLSTM的所有输出都被连接起来，并与实际的PM2.5数据进行比较。所有BiLSTM都具有相同的内部结构。

4、文章解读

1、Introduction

PM2.5的预测方法主要有两类，即数值模型和统计模型，数值模拟方法通常更实用，提供系统的预测结果，然而，它需要详细和精确的区域气候，统计建模，特别是集成机器学习和深度学习技术的模型，吸引了来自各个领域的广泛科学家的关注。在这项研究中，提出了前沿的双向长短期记忆神经网络（BiLSTM）来预测PM2.5的时间序列数据。BiLSTM的原理是每个训练序列包括两个LSTM神经元序列（前向和后向），两者都连接到同一个输出层。BiLSTM有效地从两个时间方向学习输入数据。此外，变分模式分解（VMD）被用来分解的PM2.5非周期信号在频域中。通过将复信号分解成多个谐波子序列来降低输入信号频域复杂度。

2、Related model

2.1VMD的特点

由于原始PM2.5数据频域波动剧烈、分布复杂，实现高精度预测具有挑战性。因此，变分模式分解（VMD）的方法被用来平稳化的输入数据。原始PM2.5数据信号自适应分解成几个固有模式函数（IMF）VMD。这种分解有效地降低了非线性和波动性，从而实现了信号稳定性

1、VMD是一种自适应的分解方法，可以根据信号的特性自动确定分解的模态数。

2、VMD可以对信号进行多尺度分解，将信号分解为不同频率范围的模态。

3、VMD能够在时域和频域上对信号进行局部化处理。它通过在优化问题中引入正则化项，使得分解的模态在时频域上具有局部化的特性，能够更好地捕捉信号的时频结构。

2.2Bidirectional LSTM的特点

1、Bidirectional LSTM通过在时间序列中同时处理正向和反向的输入，从而获得双向的上下文信息。

2、Bidirectional LSTM使用长短期记忆（LSTM）单元作为其基本构建块。LSTM单元具有记忆单元和门控机制，可以有效地处理长期依赖关系，并且能够避免梯度消失或梯度爆炸的问题。      3、Bidirectional LSTM能够对序列数据进行上下文建模，捕捉序列中的时间依赖关系。它可以学习到序列中的局部和全局模式，并且能够根据上下文信息进行准确的预测。

4、Bidirectional LSTM可以自动学习输入数据的特征表示。通过多层堆叠的LSTM单元，它可以逐渐提取出更高级别的抽象特征，从而更好地表示输入数据。

3、discussion

3.1为什么选择BiLSTM而不选择LSTM？

从图中可以看出，BiLSTM模型由前向LSTM和后向LSTM组成。这使得它分别获得当前时间的前向和后向特性，并且与LSTM相比，BiLSTM的输出更受前后数据的影响。由于空气质量数据随时间波动显著，且与前后状态有很强的相关性。所以选择BiLSTM而不选择LSTM。

4、Evaluation metric

在实验中使用了五个评价指标。评价指标包括平均绝对误差（MAE）、均方根误差（RMSE）、平均绝对百分比误差（MAPE）、决定系数（R2）和预测趋势准确度（ACC）。预报性能评价如下：

采用MAE、RMSE和MAPE对预测结果的误差水平进行评估。值越小，预测效果越准确。R2用于评估预测结果与总体原始数据的拟合程度。数值越大，数据拟合度越高，预测效果越好.ACC是用来评估模型的预测精度的趋势在短期内。

从图中可以看出，VMD与BiLSTM的结合的各方面表现性能都远好于其他模型。

5、Experimental process and results

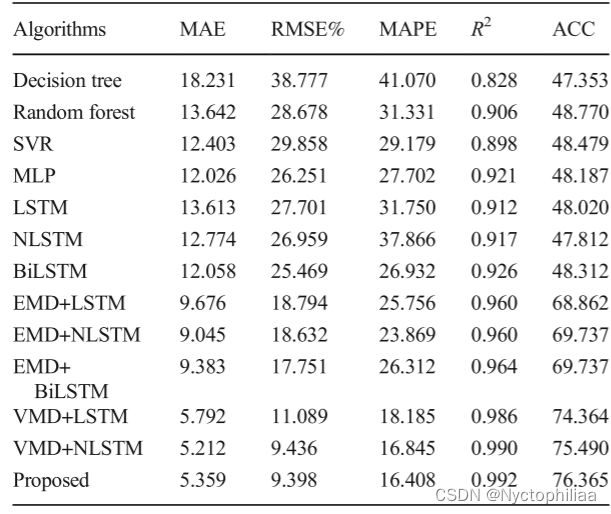
每个BiLSTM的实际实现中的超参数包括epoch=16，dropout=0.1，output_dim=64，activation ='linear'，validation_split=0.05，learning rate=0.001（static），decay=0。首先确定K值，K值决定了原始时间序列数据的IMF分解次数。采用5个评价指标和训练时间对VMDBiLSTM在不同K值下的预测性能进行了评价。结果如下：

由表1可知，随着K值的增加，预测性能不断提高，并有趋于饱和的趋势。另外，随着K的增加，计算量和时间的消耗又增加了。为了保证理想的预测效果和降低计算成本，实验中最终选择分解数K= 8。

结果表明，所提出的VMD-BiLSTM预测方法上级其他对比预测方法，具体表现在预测误差小、与真实的数据拟合度高、趋势预测精度高、模型稳定性高、泛化能力强。

6、Conclusion

考虑到PM2. 5浓度数据的非线性、非周期、非平稳等复杂特性，提出了一种混合神经网络VMD-BiLSTM模型，用于进行精确的小时前时间序列预测。

二、用pytorch 实现线性回归

 一、numpy中的自动广播机制

不同维度的矩阵，是不能直接进行加法的
所以，在numpy中，会 把维度小的向量，自动复制成维度大的向量

二、举例

通常，使用pytorch深度学习有四步

1、准备数据集（Prepare dataset）
2、设计用于计算最终结果的模型（Design model）
3、构造损失函数及优化器（Construct loss and optimizer）
4、设计循环周期（Training cycle）——前馈、反馈、更新
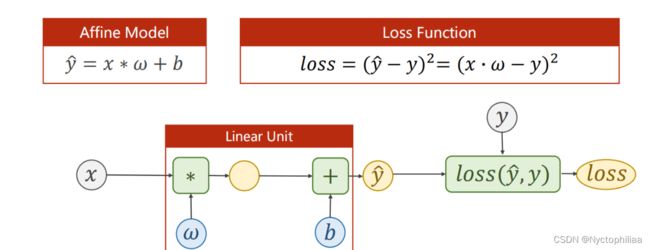
举例：线性模型
1、准备数据集
在原先的题设中，
在pytorch中，若使用mini-batch的算法，一次性求出一个批量的，则需要x 以及作为矩阵参与计算，此时利用其广播机制，可以将原标量参数ω 扩写为同维度的矩阵[ w ],参与运算而不改变其Tensor的性质。对于矩阵，行表示样本，列表示特征

import torch
#数据作为矩阵参与Tensor计算
x_data = torch.Tensor([[1.0],[2.0],[3.0]])
y_data = torch.Tensor([[2.0],[4.0],[6.0]])

2、设计模型

线性单元函数，构造计算图，损失函数。

#固定继承于Module
class LinearModel(torch.nn.Module):
    #构造函数初始化
    def __init__(self):
        #调用父类的init
        super(LinearModel, self).__init__()
        #Linear对象包括weight(w)以及bias(b)两个成员张量
        self.linear = torch.nn.Linear(1,1)

    #前馈函数forward，对父类函数中的overwrite
    def forward(self, x):
        #调用linear中的call()，以利用父类forward()计算wx+b
        y_pred = self.linear(x)
        return y_pred
    #反馈函数backward由module自动根据计算图生成
model = LinearModel()

3、构造损失函数及优化器

直接调用pytorch中的函数——均方损失函数

criterion = torch.nn.MSELoss(size_average=False)

优化器：

#model.parameters()用于检查模型中所能进行优化的张量
#learningrate(lr)表学习率，可以统一也可以不统一
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

4、设计循环周期

模型训练：

1、前馈计算预测值与损失函数

2、forward前馈计算预测值即损失loss

3、梯度或前文清零并进行backward

4、更新参数

for epoch in range(100):
    #前馈计算y_pred
    y_pred = model(x_data)
    #前馈计算损失loss
    loss = criterion(y_pred,y_data)
    #打印调用loss时，会自动调用内部__str__()函数，避免产生计算图
    print(epoch,loss)
    #梯度清零
    optimizer.zero_grad()
    #梯度反向传播，计算图清除
    loss.backward()
    #根据传播的梯度以及学习率更新参数
    optimizer.step()

测试模型

 #Output
print('w = ', model.linear.weight.item())
print('b = ', model.linear.bias.item())

#TestModel
x_test = torch.Tensor([[4.0]])
y_test = model(x_test)

print('y_pred = ',y_test.data)

三、完整代码展示

详细过程

本次代码的主要任务是利用torch包的requires_grad自动求导，构建反向传播模型：
1、导入numpy、matplotlib、os、torch库；

2、导入数据 x_data 和 y_data，注意这里有变化，用到了torch中的Tensor格式，与上次课程任务相同，所以才会出现data和grad的重要区别；

3、创建LinearModel类模型：

3.1 初始化init中，只有一个linear函数；注意要提前继承（这一步直接写，不深究）；
3.2前向传播forward方法，这是把之前的前向传播函数，拿进来做了类中的一个方法，返回预测值；
4、实例化一个模型model；

5、创建损失函数：通过调用torch.nn库中的MSELoss实现；

6、创建优化器：通过调用torch.optim库中的SGD实现；

7、创建两个空列表，因为后面绘图的时候要用：

8、创建循环，开始训练：循环的次数epoch可以自定义

9、用模型model计算；
9.1、损失loss用创建好的损失函数计算；
9.2、先用优化器对梯度清零（重要，要清楚什么时候该清零，为什么清零，原理是什么）；
9.3、令损失反向传播loss.backward；
9.4、执行一步权重更新操作，用到的函数optimizer.step( )很奇特，这里非常关键，理解起来不容易，见下面的链接；
9.5、在循环中要把计算的结果，放进之前的空列表，用于绘图；

在获得了打印所需的数据列表只有，模式化地打印图像：

代码

#!usr/bin/env python
# -*- coding:utf-8 _*-
"""
@author: 24_nemo
@file: 05_LinearRegressionwithPyTorch_handType.py
@time: 2022/04/08
@desc:
"""
import matplotlib.pyplot as plt
import torch

import os
os.environ['KMP_DUPLICATE_LIB_OK'] = 'True'

x_data = torch.Tensor([[1.0], [2.0], [3.0]])
y_data = torch.Tensor([[2.0], [4.0], [6.0]])


class LinearModel(torch.nn.Module):
    def __init__(self):
        super(LinearModel, self).__init__()
        self.linear = torch.nn.Linear(1, 1)

    def forward(self, x):
        y_hat = self.linear(x)
        return y_hat


model = LinearModel()

criterion = torch.nn.MSELoss(size_average=False)
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

loss_list = []
epoch_list = []

for epoch in range(1000):
    y_hat = model(x_data)
    loss = criterion(y_hat, y_data)
    print(epoch, loss.item())

    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    epoch_list.append(epoch)
    loss_list.append(loss.item())

print('w =', model.linear.weight.item())
print('b =', model.linear.bias.item())

x_test = torch.Tensor([[4.0]])
y_test = model(x_test)

print('y_hat =', y_test.data)
print('y_hat =', y_test.item())

plt.plot(epoch_list, loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

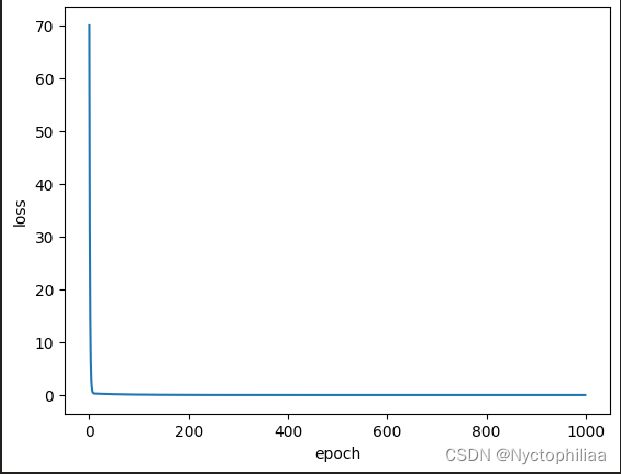
运行结果如下：

总结

通过本周的学习，初步了解了VMD和BiLSTM的特点，集成VMD的预测模型优于集成EMD的预测模型。在所有集成VMD的模型中，所提出的VMD-BiLSTM模型是最稳定的预测方法。下周我将对CNN的内容进行深度学习。