直接插入、折半插入、希尔排序

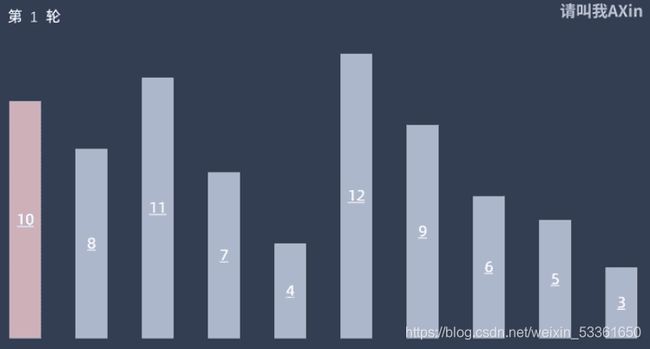
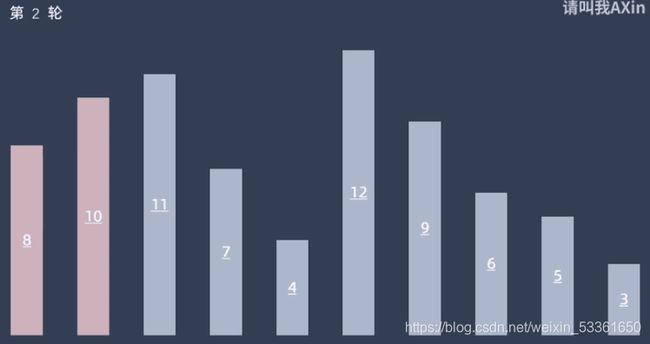
   插入排序的思想：每一趟将一个待排序的记录，按其关键字的大小插入到已经排好序的一组记录的适当的位置上，直到所有待排序记录全部插入为止。
   简单来说：就好比斗地主手里拿了一幅扑克牌，你要从前往后整理成有序的牌，则每抓一张牌，就插到合适的位置，直到抓完牌为止，即可得到一个有序序列；
  可以选择不同的方法在已排好序的记录中寻找插入位置。根据查找方式的不同，主要有三种排序方式：直接插入排序、折半插入排序和希尔排序。

想看交换排序点击上篇博客：冒泡排序和快速排序

一、直接插入排序

  直接插入排序（Straight Insertion Sort） ：是一种最简单的排序方法，将一个记录插入到已经排好序的有序表中，从而得到一个新的、记录数量增1的有序表。简单来说就是整理一副扑克牌的过程，就是一副牌从第二张牌开始抽出来看比前面的大还是小，放到合适的位置，第三张继续比较往前面找合适的位置，第四、第五…这样比较好的数就构成了有序序列，后面还没比较的就是无序的，继续往前找合适位置，直到变成一个有序数组为止

• 第一轮，从第二个数开始比较
  
• 第二个数比第一个小，把8放到10前面
  
• 11比较完不用动，比较7放到8前面
  
  这样一直插入排序，直到排序完成
  

1. 代码展示

#include 

void printf_array(int a[], int n)
{	
	for (int i = 0; i < n; i++)
	{
		printf("%d\t", a[i]);
	}
	printf("\n");
}
void insertion_sort(int a[], int n)
{
	printf_array(a, n);
	for (int i = 1; i < n; i++) //我们是从第1个开始，因为第0个本身就是有序的
	{
		int key = a[i]; //取出要比较的元素
		int j = i - 1;  //定义i前面的一个数的位置，拿出i位置的数从i-1个位置（i的前一个数位置）
		while(j >= 0 && a[j] > key) //j位置开始从后往前比较，如果大于key，大的元素就往后挪
		{
			a[j + 1] = a[j];//将j位置上的数往后挪一位
			j--;  //j递减，即下一轮循环继续往前找合适的位置
		}
		a[j + 1] = key; //j--了，碰到比key小的数了，条件不满足循环结束，这里就插入数字
		printf_array(a, n);
	}
}
int main(void)
{
	int a[] = { 10,29,8,43,1,4,8,32,55,100 };
	insertion_sort(a, 10);
	return 0;
}

2. 排序优化

缺点:

• 1）挨个儿比较
  -2） 移动元素往后挪

优化方案：

• 1）折半插入排序
• 2）希尔排序

3. 时空分析

• 时间复杂度：O(n^2) ，最好O(n)
• 空间复杂度：O(1)
• 稳定排序

---

二、折半插入排序

  上一节介绍了直接插入排序算法的理论实现和具体的代码实现，如果你善于思考就会发现该算法在查找插入位置时，采用的是顺序查找的方式，而在查找表中数据本身有序的前提下，可以使用折半查找来代替顺序查找，这种排序的算法就是折半插入排序算法。

算法思想

• 1）找插入位置
  待查找范围下标【low,high】
  找出中间元素mid = (low + high)/2
  根据结果调整查找范围（改变low或者high）
  重复
• 2）插入操作
  先挪元素
  插入操作

1. 代码实现

#include 
void print(int a[], int n, int i) {
    printf("%d:", i);
    for (int j = 0; j < n; j++) {
        printf("%d", a[j]);
    }
    printf("\n");
}
void InsertSort(int a[], int size) {
    int i, j, low = 0, high = 0, mid;
    int temp = 0;
    for (i = 1; i < size; i++) {
        low = 0;
        high = i - 1;
        temp = a[i];
        //采用折半查找法判断插入位置，最终变量 low 表示插入位置
        while (low <= high) {
            mid = (low + high) / 2;
            if (a[mid] > temp) {
                high = mid - 1;
            }
            else {
                low = mid + 1;
            }
        }
        //有序表中插入位置后的元素统一后移
        for (j = i; j > low; j--) {
            a[j] = a[j - 1];
        }
        a[low] = temp;//插入元素
        print(a, 8, i);
    }

}
int main() {
    int a[8] = { 3,1,7,5,2,4,9,6 };
    InsertSort(a, 8);
    return 0;
}

2.时空分析

折半插入排序算法相比较于直接插入排序算法，只是减少了关键字间的比较次数，而记录的移动次数没有进行优化，所以该算法的时间复杂度仍是 O(n2)

• 时间复杂度：O(n^2) ，最好O(n)
• 空间复杂度：O(1)
• 稳定排序

---

三、希尔排序

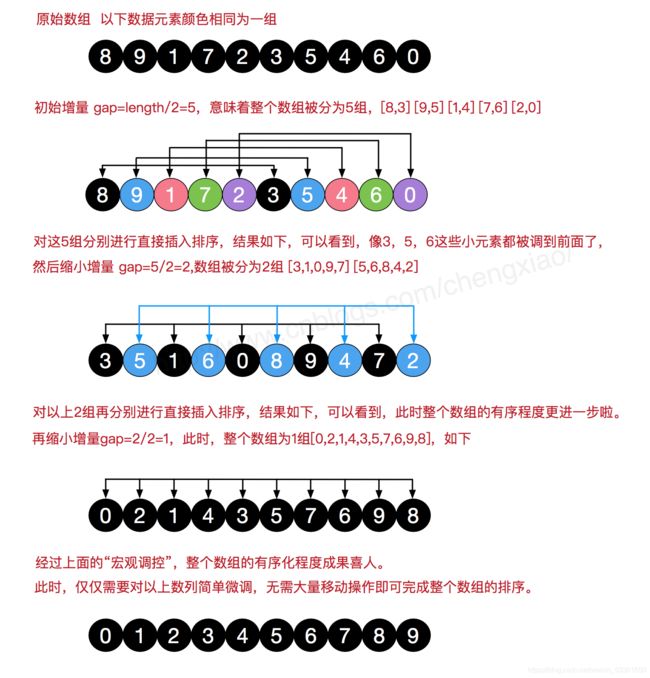
  希尔排序（Shell Sort）又称为“缩小增量排序”，是插入排序的一种。直接插入排序，当排序的记录个数少且待排序序列的关键字基本有序时，效率较高；希尔排序基于以上两点，从“减少记录个数”和“序列基本有序”两个方面对直接插入排序进行了改进。

算法思想：

因为每趟排序的间隔缩小，所以“希尔排序”又叫“缩小增量排序”

1. 代码展示

希尔排序是在直接插入排序的基础上做的改进，也就是将未排序的序列按固定增量分成若干组，等距者在同二组中，然后再在组内进行直接插入排序。这里面的固定增量从 n/2 开始，以后每次缩小到原来的一半。

#include 

void print_arr(int arr[], int n)
{
    for (int i = 0; i < n; i++)
    {
        printf("%d\t", arr[i]);
    }
    printf("\n");
}

//希尔排序
void shell_sort(int arr[], int n)
{
    int i, j, inc, key;
    //初始增量时n/2 ,每一趟之后除以2
    for (inc = n/2; inc > 0; inc /= 2)
    {
        //每一趟采用插入排序
        for (i = inc; i < n; i++)
        {
            key = arr[i];
            for (j = i; j >= inc && key < arr[j - inc]; j -= inc)//j-=inc是步长；比较前一个数和j位置这个数，如果小与前一个数，则需要将前一个数给值赋值给j位置
            {
                arr[j] = arr[j - inc];      //（增量）前一个数 > （增量）这个数 ，需要插入排序赋值
            }
            arr[j] = key;    //如果 前一个 < 这个数，则不变，就把key值赋给原来的j位置就行

        }
    }
}

int main()
{
    int arr[] = {15,5,2,7,12,6,1,4,3,8,9,18};
    printf("排序前：\n");
    print_arr(arr, 12);
    shell_sort(arr, 12);
    printf("排序后：\n");
    print_arr(arr, 12);
    return 0;
}

2. 时空分析

• 时间复杂度：n(log₂n)^2
• 空间复杂度：O(1)
• 不稳定排序