LeetCode 494.目标和 (动态规划 + 性能优化)二维数组 压缩成 一维数组
494. 目标和 - 力扣(LeetCode)
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1 输出:1
思路整理:可以将集合分为两个集合,一个加法集合(left),一个减法集合(right)
可以求出加法集合(left),将问题转换为求出left这个集合。详细讲解看下文~
left:表示加法集合
right:表示减法集合
left + right = sum
left - right = target
left = (sum + target) / 2
集合{1 1 1 1 1},分成left 和 right,生成的target如下:
left(加法集合) right(减法集合) target
4 1 -3
3 2 1
2 3 -1
1 4 -3
sum = 5
left = (sum + target) / 2
(O_O)?
发现并没有target = 2,于是当target = 2时,left = (2+5)/2 = 7/2 无法整除,
也就是 7 % 2 == 1 直接就 return 0 就好了
表示找不出这样的集合能满足 left - right = target
此时问题转化为求出left这个集合,也就是说这个容器,
问在这个集合里边的所有元素装满这个容器有多少种方法?(妙啊~)
有多少个元素能装满这个容器,我们就能找到符合这个题目条件的多少种
组合。此时发现这有点类似背包问题。那么left就是背包的容量,
集合{1 1 1 1 1}是物品集合
例子: nums = [1,2,1,3,1],target = -2,当这种情况的时候,left=3
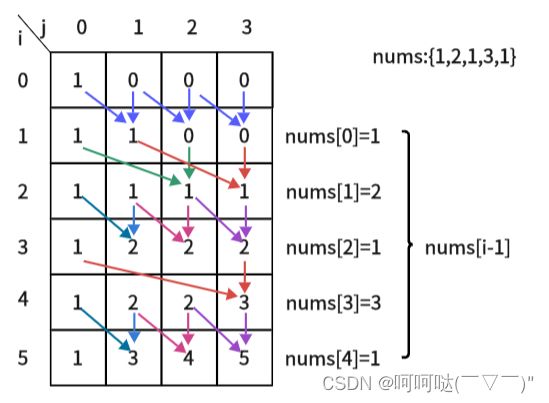
(1)二维dp数组
dp[i][j] 表示在数组 nums 的前 i 个数中选取元素,使得这些元素之和等于 j 的方案数
比如说我们要计算元素之和 等于 3 的方案数,由于
0 + 3 = 3
1 + 2 = 3
2 + 1 = 3
所以我们可以把元素之和 等于 0,1,2的方案数分别计算出来,然后再相加就可以得到元素之和等于3的方案数。
当nums[0]=1时,
- nums[0]放不进去容量为0的背包
j=0,j j=1,j>=nums[0],那么dp[1][1] = dp[0][1] + dp[0][1-nums[0]] = 0 + dp[0][0] = 0 + 1 = 1 j=2,j>=nums[0],那么dp[1][2] = dp[0][2] + dp[0][2-nums[0]] = 0 + dp[0][1] = 0 + 0 = 0 j=3,j>=nums[0],那么dp[1][3] = dp[0][3] + dp[0][3-nums[0]] = 0 + dp[0][2] = 0 + 0 = 0 以此类推~ 思考 思考,压缩状态,将二维dp数组 优化为 一维dp数组 将二维dp数组压缩成一维dp数组!!! (重复利用实现滚动数组)
当 j < nums[i-1]时
① dp[i][j] = dp[i-1][j]; //"copy"
当j >= nums[i-1]时
② dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]];
将①和②整合起来
dp[i][j] = dp[i-1][j];
if(j>=nums[i-1]) {
dp[i][j] += dp[i-1][j-nums[i-1]];
}// 二维dp数组
class Solution {
public:
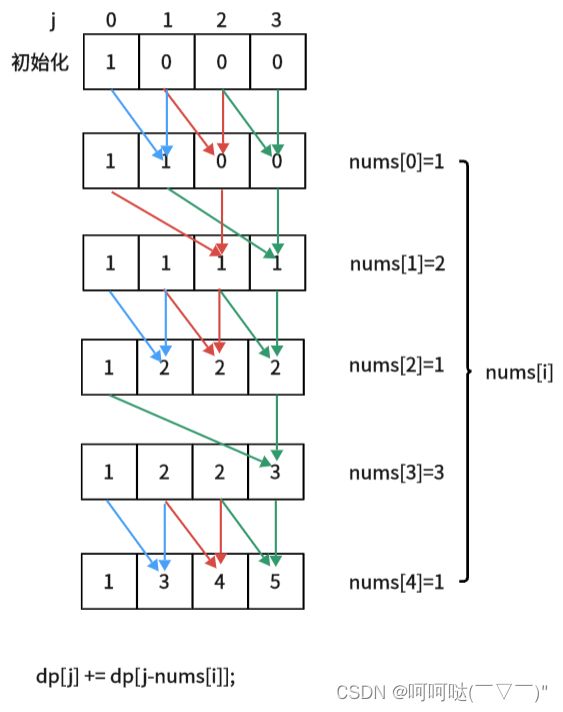
int findTargetSumWays(vectordp[j] += dp[j-nums[i]];
dp[j] 装满容量为j的背包 有dp[j]种方法
↑
dp[j-nums[i]]
nums[i] dp[j-nums[i]]
1 dp[4] 凑成 dp[5]
2 dp[3] 凑成 dp[5]
3 dp[2] 凑成 dp[5]
4 dp[1] 凑成 dp[5]
5 dp[0] 凑成 dp[5]
dp[5] = dp[4] + dp[3] + dp[2] + dp[1] + dp[0]
也就是dp[j] += dp[j-nums[i]];
初始化:dp[0] = 1
集合{0} target = 0 此时dp[0] = 1// 一维dp数组
class Solution {
public:
int findTargetSumWays(vector