89搜索算法bfs

BFS基础知识

这篇博客介绍的很详细。

BFS经典问题

走迷宫

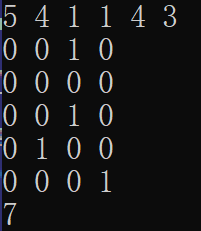
输入地图n、列数m、起点(sx,xy)、终点(ex,ey)
输入n行m列地图，0代表可以走，1代表有障碍物不能走
输出从起点到终点的最短步数

#include
using namespace std;

int n, m, sx, sy, ex, ey;
int a[100][100]; //地图
int b[100][100]; //标记数组
int d[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; 
struct node {
	int x;
	int y;
	int step;
	node(int xx, int yy, int stepp) { //构造方法 
		x = xx;
		y = yy;
		step = stepp;
	}
};
queue <node> q;

void bfs(int x, int y, int step) {
	//起点入队
	b[sx][sy] = 1;
	q.push(node(x, y, step));
	
	//维护队列
	while (!q.empty()) {
		//记录队头，队头出队
		node tmp = q.front(); 
		q.pop();
		
		//如果队头是终点
		if (tmp.x == ex && tmp.y == ey) {
			cout << tmp.step << endl;
			return;
		} 
		
		//可扩展点入队
		for (int i = 0; i < 4; i++) {
			int nx = tmp.x + d[i][0];
			int ny = tmp.y + d[i][1];
			int nstep = tmp.step + 1;
			if (nx >= 1 && ny >= 1 && nx <= n && ny <= m && !a[nx][ny] && !b[nx][ny]) {
				//在地图内、没有障碍物、没走过
				b[nx][ny] = 1;
				q.push(node(nx, ny, nstep));
			}
		} 
	} 
}

int main()
{
	cin >> n >> m >> sx >> sy >> ex >> ey;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			cin >> a[i][j];
		}
	}
	bfs(sx, sy, 0);
	return 0;
} 

样例输入输出：

炸弹人游戏

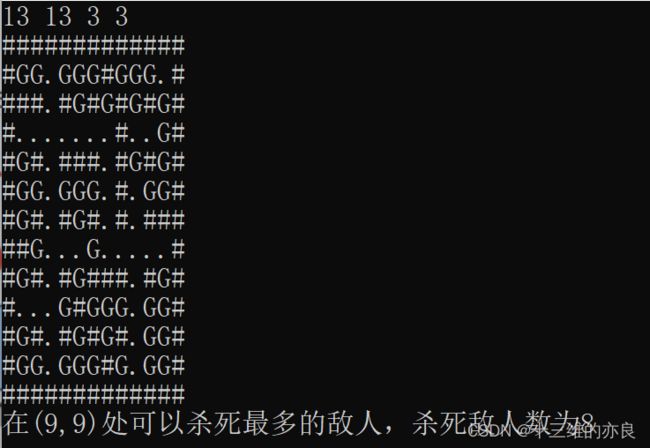
小S的小霸王游戏机里有一款炸弹人游戏。地图由硬砖块、软砖块、敌人组成。小S在(x,y)处，他可以移动，但不能移动到砖块和敌人的位置。现在小S要在某一空地放置一个炸弹，使得消灭的敌人数最多（炸弹可以消灭同行同列的敌人，但是不能炸砖块，硬砖软砖都不行）。
输入：行数n，列数m，小S的位置(x,y)
n行m列的地图（#代表砖头，G代表怪兽，.代表空地）
输出：坐标值

#include
using namespace std;

char a[100][100]; //地图
int  b[100][100]; //标记数组
int  d[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; //方向数组
int n, m, x, y; 
int ans, ans_x, ans_y;
struct node {
	int x;
	int y;
	node(int xx, int yy) { //构造方法
		x = xx;
		y = yy;
	} 
}; 
queue <node> q;

int getNum(int i, int j) {
	int he = 0;
	//向上统计 
	int tmpi = i; int tmpj = j;
	while (a[tmpi][tmpj] != '#') {
		if (a[tmpi][tmpj] == 'G') he++;
		tmpi--;
	}
	
	//向下统计
	tmpi = i; tmpj = j;
	while (a[tmpi][tmpj] != '#') {
		if (a[tmpi][tmpj] == 'G') he++;
		tmpi++;
	}
	
	//向坐统计
	tmpi = i; tmpj = j;
	while (a[tmpi][tmpj] != '#') {
		if (a[tmpi][tmpj] == 'G') he++;
		tmpj--;
	}
	
	//向右统计
	tmpi = i; tmpj = j;
	while (a[tmpi][tmpj] != '#') {
		if (a[tmpi][tmpj] == 'G') he++;
		tmpj++;
	}
	return he;
}

void bfs(int x, int y) {
	//起点入队
	q.push(node(x, y));
	b[x][y] = 1;
	
	//维护队列
	while (!q.empty()) {
		//记录队头，队头出队
		node tmp = q.front();
		q.pop();
		
		//判断队头
		if (getNum(tmp.x, tmp.y) > ans) {
			ans = getNum(tmp.x, tmp.y);
			ans_x = tmp.x;
			ans_y = tmp.y;
		} 
		
		//可扩展点入队
		for (int i = 0; i < 4; i++) {
			int nx = tmp.x + d[i][0];
			int ny = tmp.y + d[i][1];
			if (nx >= 0 && ny >= 0 && nx < n && ny < m && a[nx][ny] == '.' && !b[nx][ny]) {
				//在地图内、没有障碍物和怪兽、没走过
				q.push(node(nx, ny));
				b[nx][ny] = 1; 
			}
		} 
	} 
}

int main()
{
	cin >> n >> m >> x >> y;
	for (int i = 0; i < n; i++) {
		cin >> a[i];
	}
	bfs(x, y);
	printf("在(%d,%d)处可以杀死最多的敌人，杀死敌人数为%d\n", ans_x, ans_y, ans);
	return 0;
}
/*
13 13 3 3
#############
#GG.GGG#GGG.#
###.#G#G#G#G#
#.......#..G#
#G#.###.#G#G#
#GG.GGG.#.GG#
#G#.#G#.#.###
##G...G.....#
#G#.#G###.#G#
#...G#GGG.GG#
#G#.#G#G#.GG#
#GG.GGG#G.GG#
#############
*/

蒜头君回家

bfs 的时候标记数组多开一维度表示是否已经取得了钥匙的状态。如果到达终点并且取得钥匙的状态被标记，bfs 结束。

所以我们需要把标记数组开成三维，第三个维度来标记是否拿到钥匙，也就是同一个点其实可以走两次，第一次是没拿到钥匙的时候，第二次是拿到钥匙的时候

#include
using namespace std;

const int N = 2000 + 5;
int n, m, sx, sy;
char a[N][N]; //地图
int  b[N][N][2]; //标记数组
int  d[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}; //方向数组 
struct node {
	int x, y;
	int step;
	int flag; //为1代表带了钥匙，为0代表没带钥匙
	node(int xx, int yy, int stepp, int flagg) {
		x = xx; y = yy; step = stepp; flag = flagg;
	} 
};
queue <node> q;

void bfs(int x, int y) {
	//起点入队
	q.push(node(x, y, 0, 0));
	b[x][y][0] = 1;
	
	//维护队列
	while (!q.empty()) {
		//记录队头，队头出队 
		node tmp = q.front();
		q.pop();
		
		
		//如果队头为终点且带了钥匙 
		if (a[tmp.x][tmp.y] == 'T' && tmp.flag) {
			cout << tmp.step << endl;
			break;
		} 
		
		//可扩展点进行入队
		for (int i = 0; i < 4; i++) {
			int nx = tmp.x + d[i][0];
			int ny = tmp.y + d[i][1];
			if (nx >= 0 && ny >= 0 && nx < n && ny < m && a[nx][ny] != '#' && !b[nx][ny][tmp.flag]) {
				//没越界、没有障碍物、没走过 
				b[nx][ny][tmp.flag] = 1;
				if (a[nx][ny] == 'P') { //如果碰见钥匙了，那么修改flag位为1 
					q.push(node(nx, ny, tmp.step + 1, 1));
				}
				else { //如果没碰见钥匙，flag位与之前相同 
					q.push(node(nx, ny, tmp.step + 1, tmp.flag));
				}
			}
		}
	} 
}

int main()
{
	//输入 
	cin >> n >> m;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < m; j++) {
			cin >> a[i][j];
			if (a[i][j] == 'S') { //记录起点坐标 
				sx = i;
				sy = j;
			}
		}
	}
	
	//bfs搜索
	bfs(sx, sy);
	return 0; 
}

一维坐标的移动

#include
using namespace std;

int n, a, b;
int v[5010]; //标记数组
struct node {
	int x, step;
	node(int xx, int stepp) {
		x = xx;
		step = stepp;
	}
}; 
queue <node> q;

void bfs(int x, int step) {
	//起点入队
	q.push(node(x, step));
	v[x] = 1;
	
	//维护队列
	while (!q.empty()) {
		//记录队头，队头出队
		node tmp = q.front();
		q.pop(); 
		
		//判断队头是否为终点
		if (tmp.x == b) {
			cout << tmp.step << endl;
			return;
		} 
		
		//可扩展结点入队
		if (tmp.x + 1 <= n && !v[tmp.x + 1]) { //前走一步 
			q.push(node(tmp.x + 1, tmp.step + 1)); 
			v[tmp.x + 1] = 1;
		} 
		if (tmp.x - 1 >= 0 && !v[tmp.x - 1]) { //后走一步 
			q.push(node(tmp.x - 1, tmp.step + 1));
			v[tmp.x - 1] = 1; 
		} 
		if (tmp.x * 2 <= n && !v[tmp.x * 2]) { //前走二倍步 
			q.push(node(tmp.x * 2, tmp.step + 1)); 
			v[tmp.x * 2] = 1;
		} 
	} 
}

int main()
{
	cin >> n >> a >> b;
	bfs(a, 0);
	return 0;
}

DFS与BFS对比

如果想学习DFS，请阅读我另一篇文章搜索算法dfs。