博弈题目总结（一）

一、POJ 1067 取石子游戏 

       有两堆石子，数量任意，可以不同。游戏开始由两个人轮流取石子。游戏规定，每次有两种不同的取法，一是可以在任意的一堆中取走任意多的石子；二是可以在两堆中同时取走相同数量的石子。最后把石子全部取完者为胜者。现在给出初始的两堆石子的数目，如果轮到你先取，假设双方都采取最好的策略，问最后你是胜者还是败者。

威佐夫博弈（Wythoff Game）

        用一个二维数组来表示玩家将面临的局面，即a[i][j]表示两堆石头分别有i个和j个，如果a[i][j]是必败局面的话，那么——这个点的右侧所有点a[i][k](k>j)都是必胜点，因为可以通过拿走第二堆的k-j个石子令对方面临必败局面a[i][j]；这个点的下侧所有点a[k][j](k>i)都是必胜点，因为可以通过拿走第二堆的k-i个石子令对方面临必败局面a[i][j]；这个点的右下方45度所有点a[i+k][j+k](k>0)都是必胜点，因为可以通过同时拿走两堆的k个石子令对方面临必败局面a[i][j]。这样如果在二维数组a[i][j]处标记”X”表示必败的话，在上面提到的三类点的位置都可以标记”O”表示必胜了，做完这项工作后，再挑选如今距离原点最近的未被标记的点，它一定是下一个必败点——因为它无法通过游戏规则移动到一个必败点，并且规则规定的动作都是朝向原点移动的，而它是距离原点最近的未被标记的点，因此它只能移动到一个必胜点从而让对方获胜，所以该点一定是下一个必败点。有了新必败点后就可以重复上述工作，直到找出问题范围内的所有必败点。

前几个必败点如下：(0，0)，(1，2)，(3，5)，(4，7)，(6，10)，(8，13)……可以发现，对于第k个必败点(m(k),n(k))来说，m(k)是前面没有出现过的最小自然数，n(k)=m(k)+k。
m(k) = k * (1 + sqrt(5))/2

n(k) = m(k) + k

int main()
{
    int n,m;
    while (cin>>n>>m)
    {
        if (n>m) swap(n,m);
        double x=(1+sqrt(5))*0.5;
        if (floor((m-n)*x)==n)puts("0");else puts("1");
    }
}

二、POJ 1740 A New Stone Game

题目大意：
对于n堆石子，每堆若干个，两人轮流操作，每次操作分两步，第一步从某堆中去掉至少一个，第二步（可省略）把该堆剩余石子的一部分分给其它的某些堆。最后谁无子可取即输。
解题思路：
1、先考虑1堆的时候，1堆当然是N点（必胜点），
2、然后考虑2堆，细想一下可以发现，当2堆一样时，这个时候的目的就是要把对方给逼到只有2堆都是1的时候，就能必胜了。但是想一下，后手只要模范先手所做的动作，那么最后就会形成两堆都是1的局势，所以当2堆相同时，是一个P点（必败点）。注意当2堆不一样的时候，先手可以把它变成一样，此时变为N点。
3、考虑3堆，这个时候，先手必定是可以把局势变成2堆相同的堆的，那么先手肯定胜利，为N点。** （发现，当堆为偶数堆两两同高的时候，此时是P点）
偶数：
4、当n >= 4堆的时候可以发现，可以把堆的高度按从小到大排列。当n为偶数的时候，可以把最高的那一堆跟最小的那一堆变成一样，然后把高度差用来平衡剩余的那些堆，注意一定是可以平衡的，因为把剩余的堆相邻两两的差值投射到y轴上发现这些离散的线段和
小于最高堆于最小堆的差值。
奇数：
5、当n >= 4堆的时候可以发现，可以把堆的高度按从小到大排列。当n为奇数的时候，可以把最高堆给去掉，然后分配给其它堆。

代码：

int main()
{
    while (~scanf("%d",&n) && n)
    {
        for (i=1;i<=n;i++)scanf("%d",&a[i]);
        sort(a+1,a+n+1);
        if (n&1)puts("1");
        else
        {
            m=0;
            for (i=2;i<=n;i+=2)
            {
                if (a[i]!=a[i-1])m=1;
            }
            if (!m)puts("0");else puts("1");
        }
    }
    return 0;
}

三 、POJ 2234  Matches Game

题目大意：
有n堆石子，每次可以从任意一堆拿任意数量的石子，至少拿1个，两人轮流进行，问先手是否必胜？

题解：

尼姆博弈，将所有数求异或，为0，必输，不为0，比胜。

代码：

int main()
{
    while (~scanf("%d",&n) && n)
    {
        t=0;
        for (i=1;i<=n;i++)scanf("%d",&a[i]),t=t^a[i];
        if (t)puts("Yes");else puts("No");

    }
    return 0;
}

四 、POJ 2348 Euclid's Game

题意：
给定两个数，两个人每次从较大数中减去较小数的倍数，谁先得到0谁获胜，为谁赢？

题解：

令一种可能出现的整数对为(a,b)，其中(b>a)。有两种情况
1.b−a2.b−a>a，可以从bb中减去至少2个a，假设可以从bb中最多可以减去x个aa，那么从bb中减去(x−1)个aa后得到状态(a,b−(x−1)∗a)，此时即为讨论的第一种情况。如果状态(a，b−(x−1)∗a)为必败态的话，那么(a,b)就是必胜态，如果状态(a,b−(x−1)∗a)为必胜态的话，那么(b−x∗a,a)肯定是必败态，所以直接减去x倍的aa，得到必败态，那么(a,b)即为必胜态。

代码：

int main()
{
    int n,m;
    while (cin>>n>>m && n)
    {
        if (nm)break;
                int t=n-m;n=m;m=t;
                num++;
            }
            if (num&1)puts("Ollie wins");else puts("Stan wins");
        }
    }
    return 0;
}

五 、HDU 1404 Digital Deletions

题意：给一个长度不超过6字符的数字字符串。两种操作二选一：
1、把任意一位变成比他本身小的数字。比如205，可以把5变成0,1,2,3,4，成了200,201.so on。
2、把任意一个0后及他本身去掉。比如205，去掉2和他后面的数字变成了2。
问最后去掉数字的算赢。问先手有木有必胜策略。
题解：可以通过SG函数的性质。暴力吧1-1e6每个数字的状态求出来。能一步到达必败状态的都为必胜点。sg[1]明显是必败点，每次从必败点去找。怎么找？
1、可以将每位上的数字+1，直到等于9.
2、如果位数小于6，可在末尾+0.再加上若干数。最后只要知道sg值是0或者1就OK了。

代码：

void dfs(int x)
{
    int len,i,j,k,n;
    n=x;len=0;
    while (n) { len++;  n/=10; }
    for (i=1;i<=len;i++)
    {
        int b=pow(10,i-1);
        j=x % (b*10) / b;
        for (k=1;k<=9-j;k++)
			if (x+k*b

六 、HDU 1524 A Chess Game

题意:
在一个有向无环图上有n个顶点,每一个顶点都只有一个棋子,有两个人,每次根据这个图只能将任意一颗棋子移动一,如果到某一步玩家不能移动时,那么这个人就输.
题解:
本题是最典型的有向无环图的博弈,利用dfs把所有顶点的SG值都计算出来,然后对每个棋子的SG值进行异或运算,如果为0就是先手必败,否则就是先手必胜.

代码：

int i,j,k,l,n,m,t,h;
vector G[N];
bool f[N];
int sg[N];

int dfs(int x)
{
    if (sg[x]!=-1)return sg[x];
    bool c[30];
    memset(c,0,sizeof c);
    int i;
    for (i=0;i

七、HDU 1517 A Multiplication Game

题意：
2 个人玩游戏，给定一个数n,从 1 开始，轮流对数进行累乘一个数（2~9中取），直到第一次等于或超过n为赢.

题解：

[n,正无穷]为必败点，因为他面对这个范围的数时已经无法操作了；

[n/9,n-1]为必胜点，因为他们都能一步到达必败点；

[n/9/2,n/9-1]为必败点，因为他们只能到达必胜点；

“/”为向上取整

代码：

int main()  
{  
    int n,x;  
    while(~scanf("%d",&n))  
    {  
        for(x=0;n>1;x++)  
        {  
            if(x&1)  
                n = ceil(n*1.0/2);  
            else  
                n = ceil(n*1.0/9);  
        }  
        puts(x&1?"Stan wins.":"Ollie wins.");  
    }  
    return 0;  
}  

八、HDU 1536 S-Nim 

题意：

告诉一个集合，每次取石子只能取集合中的个数，多个询问，告诉每堆石子的个数，问先手是否必胜。

题解：

SG函数。预处理出来所有可能堆数的SG函数，询问时直接异或。

代码：

int sg[N];
int i,j,k,l,n,m,t,h,a[110];

int dfs(int x)
{
    if (sg[x]!=-1)return sg[x];
    bool c[101]={0};
    for (int i=1;i<=n;i++)
    {
        int t=x-a[i];
        if (t<0)break;
        sg[t]=dfs(t);
        c[sg[t]]=1;
    }
    for (int i=0;;i++)if (!c[i])return i;
}

int main()
{
    while (~scanf("%d",&n) && n)
    {
        memset(sg,-1,sizeof sg);
        for (i=1;i<=n;i++) scanf("%d",&a[i]);
        sort(a+1,a+n+1);
        for (i=0;i

九、HDU 1536

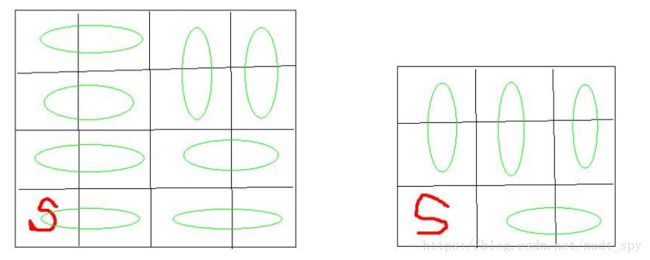
从一个n*n的角落出发，每次移动到相邻的，而且没有经过的格子上。谁不能操作了谁输。

结论就是n为偶数，先手赢，奇数，后手赢。

S表示起点。如果n为偶数，那么所有格子可以被2*1的砖块覆盖掉。这样先手每次都移动到当前1*2的另外一块。先手必赢。

如果n为奇数。出了起始那个点，其余点都可以被覆盖。所以后手赢。

代码：

int main()
{
    int n;
    while (~scanf("%d",&n) && n)
    {
        if (n&1)puts("ailyanlu");else puts("8600");
    }
    return 0;
}

十、HDU 1729 Stone Game 

题意：

有n个箱子，每个箱子有一个容量，两人轮流想箱子里放石子，每次放的个数不能超过那个箱子里已经有的石子的个数。问先手必胜还是必败。

题解：

首先，约定（a,b）表示容量为a的箱子，当前有b个石子在里面。

求必败态。

首先（S,S）为必败态。设p=max{x | x*x+x

下一个必败态:（p,t）,其中t=max{x | x*x+x

下一个必败态:（t,k）,其中k=max{x | x*x+x

.......

用递归求解，每一个必败态（a,b），如果c==b,必败，如果c>b，则SG值为a-c,如果c

代码：

int dfs(int a,int b)
{
    int t=sqrt(a);
    while (t+t*t>=a)t--;
    if (b>t)return a-b;else return dfs(t,b);
}
int main()
{
    int n,tt=0;
    while (~scanf("%d",&n) && n)
    {
        int ans=0;
        for (int i=1;i<=n;i++)
        {
            int j,k;
            scanf("%d%d",&j,&k);
            ans=ans^dfs(j,k);
        }
        if (ans)printf("Case %d:\nYes\n",++tt);
        else printf("Case %d:\nNo\n",++tt);
    }
    return 0;
}