【博弈论笔记】第二章 完全信息静态博弈

此部分博弈论笔记参考自经济博弈论（第四版）/谢识予和老师的PPT，是在平时学习中以及期末备考中整理的，主要注重对本章节知识点的梳理以及重点知识的理解，细节和逻辑部分还不是很完善，可能不太适合初学者阅读（看书应该会理解的更明白O(∩_∩)O哈哈~）。现更新到博客上供大家浏览，希望能够帮助到正在学习博弈论的大家。

第二章 完全信息静态博弈

各博弈方同时选择策略，且每一个博弈方对其他所有博弈方的特征、策略和得益等有关博弈的所有信息都完全了解的博弈，称为完全信息静态博弈。

2.1 基本分析思路和方法

2.1.1 上策均衡

在一个博弈中，不管其它博弈方选择什么策略，一博弈方的某个策略给他带来的得益总能严格高于其它策略，该策略称为博弈方的上策。

例如：囚徒困境——“坦白”；双寡头削价——“低价”

在一个博弈的某个策略组合中，如果所有策略都是各博弈方的上策，那么这个策略组合就是该博弈的上策均衡。

例如：囚徒困境——（坦白，坦白）

分析博弈时，应该先判断各博弈方是否有上策，博弈是否存在上策平衡。

2.1.2 严格下策反复消去法

不管其它博弈方的策略如何变化，如果一个策略给一个博弈方带来的得益总是比其他策略带来的得益要小，那么这个策略就是该博弈方的严格下策。

严格下策反复消去法 特点：既可在同一博弈方的策略空间反复运用，也可在不同博弈方的策略空间交叉运用

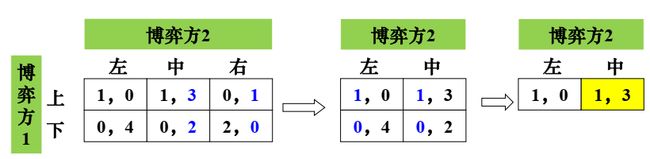
策略之间不一定存在绝对优劣关系，往往只存在相对优劣关系

2.1.3 划线法

找出针对其他博弈方每种策略的最佳对策

例1：

当博弈方1选择上时，博弈方二在左中右对比一看，应选择"中"的收益3；当博弈方1选择下时，博弈方二在左中右对比一看，应选择"左"的收益4。最终画完后发现策略组合（1，3）是稳定的。

例2：

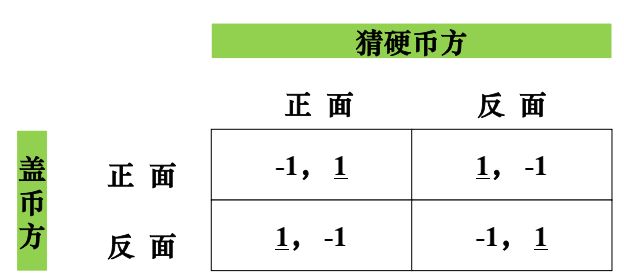
不存在两个数字下都划有短线的得益数组，因此没有相互的最佳策略。

例3：夫妻之争

夫妻有两张时装表演票和同一时间的两张足球比赛票，但偏好不同。

2.1.4 箭头法

两种策略组合都是均衡策略。但划线法不能确定哪个结果会出现$⟶$不能完全解决问题。

例1：（坦白，坦白）没有指离箭头，是稳定的

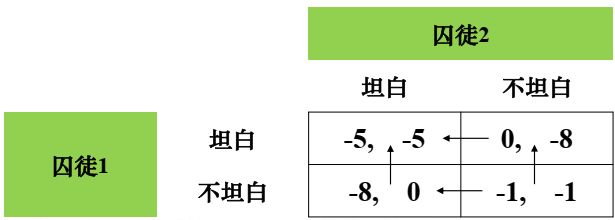
例2：两个策略组合的得益组数只有指向箭头，没有指离的箭头。两个稳定的策略组合，难以判断博弈结果。

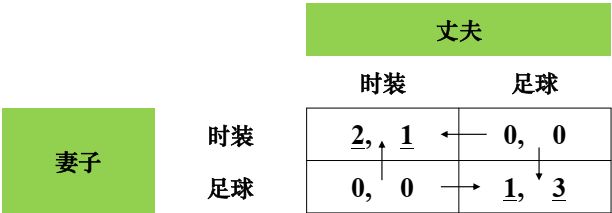
在每个策略组合处，若博弈方能通过单独改变自己的策略增加得益，那么就引一箭头，最后综合分析寻找均衡

2.2 纳什均衡

2.2.1 纳什均衡的诞生

1949年10月纳什证明了一个质疑亚当·斯密（市场看不见的手，会自动调节市场经济）、挑战冯·诺依曼（冯诺依曼提出的最大最小定理：任何时候，两人参与的零和博弈总存在一个“能使博弈方可能的最小收入最大化” 的均衡策略组合，纳什将其推广为博弈方无论多少都适用，也不仅仅限于零和博弈)的崭新理论。

2.2.2 纳什均衡的定义

定性定义：给定其他博弈方策略的条件下，每个博弈方选择自己的最优策略，所有博弈方选择的最优策略构成一个策略组合，该策略组合就是纳什均衡。

数学定义：在博弈 $G=\left\{S_1,\dots ,S_n;u_1,\dots ,u_n\right\}$ 中, 如果由各博弈方的策略组成的策略组合 $\left(s_1{}^{\ast },\dots ,s_n{}^{\ast }\right)$ 中, 任一博弈方 $i$ 的策略 $s_i{}^{\ast }$, 都是对其余博弈方策略的组合 $(s_1{}^{\ast }$, $\dots ,s_{i-1}{}^{\ast },s_{i+1}{}^{\ast },\dots ,s_n{}^{\ast })$ 的最佳对策, 也即 $u_i(s_1{}^{\ast },\dots ,s_{i-1}{}^{\ast }$, $s_i^{\ast },s_{i+1}{}^{\ast },\dots ,s_n^{\ast })\ge u_i\left(s_1{}^{\ast },\dots ,s_{i-1}^{\ast },s_{ij},s_{i+1}{}^{\ast },\dots ,s_n{}^{\ast }\right)$ 对任意 $s_{ij}\in S_i$ 都成立, 则称 $\left(s_1{}^{\ast },\dots ,s_n{}^{\ast }\right)$ 为博弈 $G$ 的一个 “纳什均衡"。

上策均衡与纳什均衡的关系：

• 上策均衡： 不管你选什么， 我选的策略是我能选的最好策略
• 纳什均衡： 给定你的策略， 我选的策略是我能选的最好策略

上策均衡一定是纳什均衡，但纳什均衡不一定是上策均衡，上策均衡是更高一级的条件。

2.2.3 纳什与严格下策反复消去法

定理2.1： 在有n个博弈方的博弈 $G=\left\{S_1,\dots ,S_n;u_1,\dots ,u_n\right\}$ 中，如果严格下策反复消去法排除了除 $\left(s_1{}^{\ast },\dots ,s_n{}^{\ast }\right)$之外的所有策略组合，那么$ \left(s_1{ }^, \ldots, s_n{ }^\right)$一定是该博弈唯一的纳什均衡。

定理2.2： 在有n个博弈方的博弈中$G=\left\{S_1,\dots ,S_n;u_1,\dots ,u_n\right\}$中，如果$\left(s_1{}^{\ast },\dots ,s_n{}^{\ast }\right)$是G 的一个纳什均衡，那么严格下策反复消去法一定不会将它消去。

两者都可由反证法证明。

两个定理保证了：

• 相容性
  严格下策反复消去法与纳什均衡分析之间的相容性；
• 可行性
  在纳什均衡分析之前，通过严格下策反复消去法简化博弈是可行的。

2.2.4 一致预测性质

如果所有博弈方预测特定博弈结果会出现，那么所有博弈方都不会选择与预测不一致的策略。

2.3 无限策略博弈和反应函数（都体现了纳什均衡）

画线法和箭头法只适用于可两两比较的有限策略博弈，分析无限策略博弈时不适用

2.3.1 连续策略的古诺博弈

假设：市场总供给： $Q=Q_1+Q_2$，市场价格： $P=P(Q)=8–Q$，平均成本： $C_1=C_2=2$

则利润为：
$$\begin{gathered} U_1=P{Q}_1-C_1{Q}_1=(8-Q)Q_1-2Q_1=6Q_1-Q_1{Q}_2-Q_1^2 \\ {U}_2=P{Q}_2-C_2{Q}_2=(8-Q)Q_2-2Q_2=6Q_2-Q_1{Q}_2-Q_2^2 \end{gathered}$$
根据纳什均衡分析，即求解：
$$\begin{gathered} \underset{q_1}{\max }\left(6q_1-q_1{q}_2^{\ast }-q_1^2\right) \\ \underset{q_2}{\max }\left(6q_2-q_1^{\ast }{q}_2-q_2^2\right) \end{gathered}$$
求偏导后得出：
$$\begin{gathered} 6-q_2^{\ast }-2q_1^{\ast }=0 \\ 6-q_1^{\ast }-2q_2^{\ast }=0 \end{gathered}$$
解得$q_1^{\ast }=q_2^{\ast }=2$，此时利润$U_1=U_2=4$

但此时只是纳什均衡，而非最优策略，当$q_1^{\ast }=q_2^{\ast }=1.5$，$U^{\ast }max=9$

但合作难以实现，（1.5， 1.5）不稳定，不是纳什均衡。（1.5, 1.5） $⟶$（2, 2）

启示:

• A.古诺模型博弈是一种囚徒困境，无法实现博弈方总体和各自的最大利益。
• B. 自由竞争经济也存在低效率问题，放任自流并非最好的政策。
• C. 政府有必要对市场进行调控和监管。

2.3.2 反应函数

类比划线法，如果一博弈方对另一博弈方每种可能策略的最佳对策构成一一对应的函数关系，那么该函数就是策略反应函数。

如：
$$\begin{gathered} \frac{1}{2}(6-q_2)=q_1 \\ \frac{1}{2}(6-q_1)=q_2 \end{gathered}$$

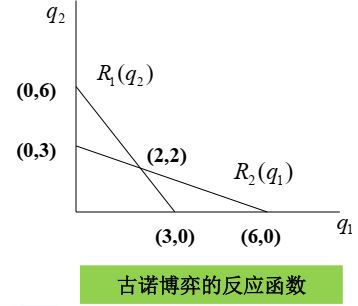
（0,3） ,（3,0）：一方不生产，另一方生产3（合作垄断） ——实现市场总利润最大化的策略组合。

纳什均衡：（2, 2）最稳定。

2.3.3 伯特兰德寡头竞价格博弈

• 产量博弈——产品无区别

• 价格博弈——产品有差别

此时各厂商选择博弈的是价格而不是产量

市场需求为：
$$\begin{array}{l}{q}_1=q_1(P_1,P_2)=a_1-b_1{P}_1+d_1{P}_2\\ q_2=q_2(P_1,P_2)=a_2-b_2{P}_2+d_2{P}_1\end{array}$$
其中$a、b$为常数，$d_1,d_2>0$表示两个厂商产品的替代因数，可以看出，$d_1$越大，$P_2$也越大时，1产品的销量上升，说明1可以取代较贵的2产品。

得益函数为：
$$\begin{array}{c}{u}_1=u_1(P_1,P_2)=P_1{q}_1-c_1{q}_1=(P_1-c_1)q_1=(P_1-c_1)(a_1-b_1{P}_1+d_1{P}_2)\\ u_2=u_2(P_1,P_2)=P_2{q}_2-c_2{q}_2=(P_2-c_2)q_2=(P_2-c_2)(a_2-b_2{P}_2+d_2{P}_1)\end{array}$$
反应函数为：
$$\begin{array}{l}{P}_1=R_1(P_2)=\frac{1}{2b_1}(a_1+b_1{c}_1+d_1{P}_2)\\ P_2=R_2(P_1)=\frac{1}{2b_2}(a_2+b_2{c}_2+d_2{P}_1)\end{array}$$
解得：
$$\begin{array}{r}{P}_1^{\ast }=\frac{d_1}{4b_1{b}_2-d_1{d}_2}(a_2+b_2{c}_2)+\frac{2b_2}{4b_1{b}_2-d_1{d}_2}(a_1+b_1{c}_1)\\ \\ P_2^{\ast }=\frac{d_2}{4b_1{b}_2-d_1{d}_2}(a_1+b_1{c}_1)+\frac{2b_1}{4b_1{b}_2-d_1{d}_2}(a_2+b_2{c}_2)\end{array}$$
实例示意图如下：

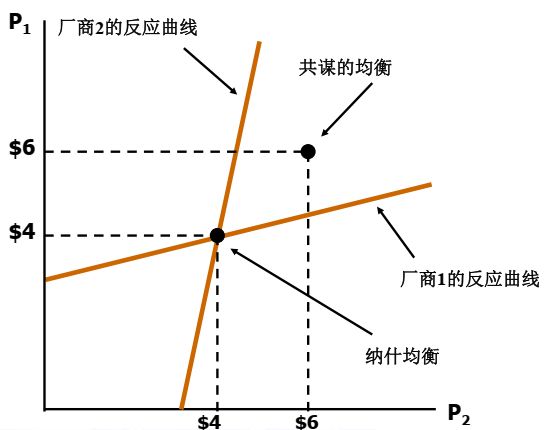
厂商为什么并不串通合作？
原因：虽然串通的利润较大，但出于私利，最终都将会降低价格以获得短期更多利润。囚徒困境

2.3.4 公共资源博弈

公共资源：任何个人或企业都不拥有所有权的自然资源，或人类生产的供大众免费使用的设施和财物。

• （1）没有个人或企业拥有所有权；
• （2）大众可自由利用

1968年，哈定思想： 若人们完全从自利动机出发自由利用公共资源，公共资源会被低效使用、过度利用、甚至浪费破坏。

以放牧为例：

每只羊的产出函数： $V＝V(Q)＝V(q_1+q_2+\dots +q_n)$（是羊群总数Q的减函数）,每只羊的成本是常数$c$

则得益函数为：$u_i=q_{i}V\left(Q\right)-q_{i}c$

给定数值例子：

假设: $n=3, c=4, V=100-(q_1+q_2+q_3) $

得益函数为：
$$\begin{array}{l}{u}_1=q_1[100-(q_1+q_2+q_3\left)\right]-4q_1\\ u_2=q_2[100-(q_1+q_2+q_3\left)\right]-4q_2\\ u_3=q_3[100-(q_1+q_2+q_3\left)\right]-4q_3\end{array}$$
反应函数为：
$$\begin{array}{l}{q}_1=R_1(q_2,q_3)=48-\frac{1}{2}{q}_2-\frac{1}{2}{q}_3\\ q_2=R_2(q_1;q_3)=48-\frac{1}{2}{q}_1-\frac{1}{2}{q}_3\\ q_3=R_3(q_1,q_2)=48-\frac{1}{2}{q}_1-\frac{1}{2}{q}_2\end{array}$$
最终：$q_1^{\ast }=q_2^{\ast }=q_3^{\ast }=24u_1^{\ast }=u_2^{\ast }=u_3^{\ast }=576$

如果是三方合作：$q_1^{\ast }=q_2^{\ast }=q_3^{\ast }=16u_1^{\ast }=u_2^{\ast }=u_3^{\ast }=768$

评价
① 农户竞争博弈——>过度放牧——>浪费资源——>未获得最好效益；

② 若农户数进一步增加，纳什均衡策略的效率更低。

③ 合作——>各农户养羊数量少——>个体和总体利益都更大；

2.3.5 反应函数存在的问题和局限性

• 问题1： 无法得到反应函数
  在有些博弈中，博弈方的策略是有限、非连续——>得益函数非连续、不可导——>无法求得反应函数。
• 问题2: 无法找到均衡
  反应函数无交点，或交点不唯一——>无法找到均衡。

2.4 混合策略和混合策略纳什均衡

2.4.1 严格竞争博弈和混合策略的引进

严格竞争博弈 : 各博弈方的利益和偏好始终不一致，在通常策略基础上没有纳什均衡的博弈。

猜硬币博弈不输原则：

• 自己的策略选择不能预先被另一方猜到
• 避免选择带规律性
• 不能有偏好

结论：最可靠的方法是以概率 p=0.5, 选正面和反面。

混合策略： 在博弈 $G=\left\{S_1,\cdots ,S_n;u_1,\cdots ,u_n\right\}$ 中, 博弈方 $i$ 的策略空间为 $S_i=\left\{s_{i1},\cdots ,s_{ik}\right\}$, 则博弈方 $i$ 以特定概率分布 $p_i=\left(p_{i1},\cdots ,p_{ik}\right)$ 在其 $k$ 个可选策略中随机选择的“策略”, 称为一个“混合策略”, 其中 $0⩽$ $p_{ij}⩽1$ 对 $j=1,\cdots ,k$ 都成立, 且 $p_{i1}+\cdots +p_{ik}=1$

纯策略的得益——确定性得益，混合策略的得益——期望得益

混合策略纳什均衡： 给定其他博弈方策略的条件下，每个博弈方选择自己的最优混合策略，所有博弈方选择的最优混合策略构成一个混合策略组合，该策略组合就是混合策略纳什均衡。此时，任何博弃方单独改变选择的概率分布，都不能增加得益。

求解原理：不向对方显示偏好，不给对方可趁之机，一个博弃方选择策略的概率分布须让对方选两个纯策略的期望得益相等。

例1：

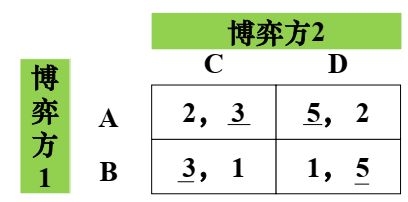
(PA, PB) 要使博弈方2选C的期望得益等于选D的期望得益： $P_A\ast 3+P_B\ast 1=P_A\ast 2+P_B\ast 5$

又因为$P_A+P_B=1$得$P_A=0.8,P_B=0.2$

同理：$P_C\times 2+P_D\times 5=Pc\times 3+P_D\times 1$, $P_C=0.8,P_D=0.2$

当双方釆用该策略组合时，虽然无法确定一次博弈的结果，但双方多次重复博弃的平均结果（期望得益）相同。

对于博弈方1的得益：
$$\begin{array}{c}{u}_1^e=p_A{p}_C{u}_1(A,C)+p_A{p}_D{u}_1(A,D)+p_B{p}_C{u}_1(B,C)+p_B{p}_D{u}_1(B,D)\\ =0.8\times 0.8\times 3+0.8\times 0.2\times 1+0.2\times 0.8\times 2+0.2\times 0.2\times 5=2.6\end{array}$$
例2 田忌赛马：

使任一方选这六种策略的收益都相同，最终齐威王和田忌都以1/6概率随机选择各自6个纯策略

Dis：

• 齐威王和田忌对任一纯策略的偏爱都会给对方可乘之机，最佳策略是以平均概率随机选择各纯策略
• 混合策略纳什均衡说明： 博弈方按各自的混合策略进行博弈，可确保在现有条件和实力下，博弈结果不会变差

例3 小偷守卫博弈

（1）问题描述：

小偷——偷/不偷，守卫——睡/不睡

博弈不存在纯策略纳什均衡，是一个非对称非零和博弃。
决策原则：应以随机方式选择策略，且选择概率不能让对方有可乘之机。——可应用纳什均衡的形式

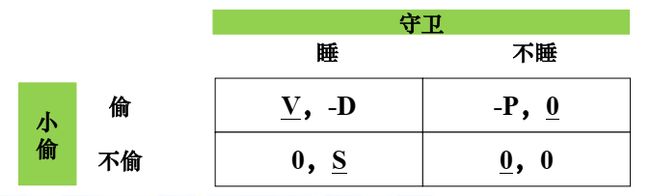
（2）小偷策略的概率分布：

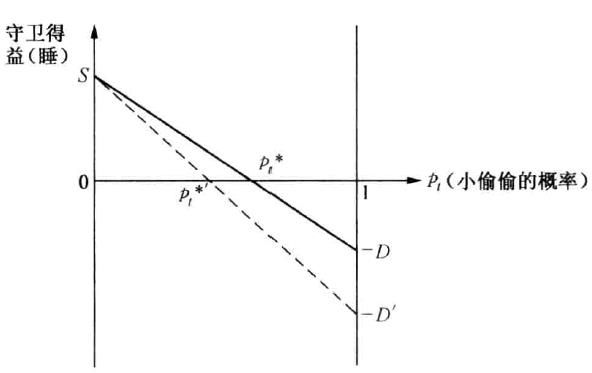
横轴为小偷选“偷”的概率p，纵轴为此时守卫选择睡的期望得益。可以看出小偷偷的概率为1时，守卫睡的得益为$-D$ ,小偷偷的概率为0时，守卫睡的得益为$S$.

小偷的最佳策略:不被抓的条件下，尽可能提高偷的概率 ，并使得守卫选择两个策略的期望得益相等,即：
$$\begin{gathered} \mathbf{S}(1-{\mathbf{p}}_{\mathbf{t}})+(-\mathbf{D}){\mathbf{p}}_{\mathbf{t}}=0 \\ 得{\mathbf{p}}_{\mathbf{t}}^{\ast }=S/(\mathbf{S}+\mathbf{D}) \end{gathered}$$
（3）激励悖论

加大对失职守卫处罚，如上图所示$D⟶D^{{}^{\prime }}$

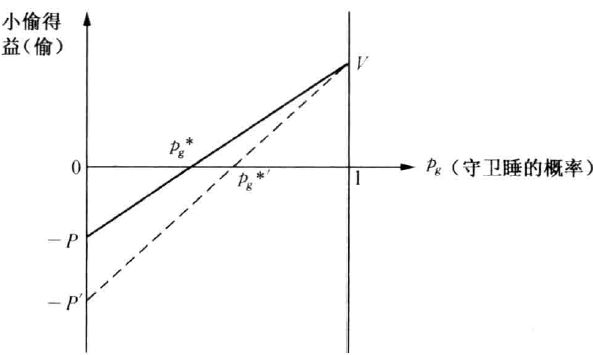
短期内，若小偷以原概率偷，守卫期望收益为负，所以守卫不会睡，之后小偷减少偷，最终达到新的平衡。新平衡下守卫不会更尽职，还是按原来的混合策略概率选择睡，只是小偷偷的概率减少了

加重对小偷的惩罚$p⟶p^{{}^{\prime }}$，小偷偷的概率不会改变，守卫会睡的更多(注意小偷偷的反应函数得出来的最佳概率点和小偷的惩罚无关，只与守卫的收益惩罚有关)

2.4.2 多重均衡博弈和混合策略

混合策略不仅适用于分析没有纯策略纳什均衡的博弈，也适用于分析有多个纯策略纳什均衡的博弈

例1 夫妻之争

妻子选择策略的概率分布应使丈夫选择两种策略的期望得益相同：
$${\text{P}}_w(\text{C})\times 1+{\text{P}}_w(\text{F})\times 0={\text{P}}_w(\text{C})\times 0+{\text{P}}_w(\text{F})\times 3$$
结果：${\mathbf{P}}_{\text{w}}\left(\mathbf{C}\right)\text{=}3/4,{\mathbf{P}}_{\text{w}}\left(\mathbf{F}\right)\text{=}1/4$

丈夫也出于这种心理选择的结果：${\mathbf{P}}_{\mathbf{h}}(\mathbf{C})=1/3,{\mathbf{P}}_{\mathbf{h}}(\mathbf{F})=2/3$

期望得益（0.67, 0.75）小于夫妻双方交流协商，任何一方迁就另一方的双方得益。夫妻之争不应该用竞争、博弈方式解决，合作、协商更好。

例2 市场机会博弈

两厂商同时发现一市场机会，若一个厂商进入，能赚100万，若两厂商同时进入，各亏50万

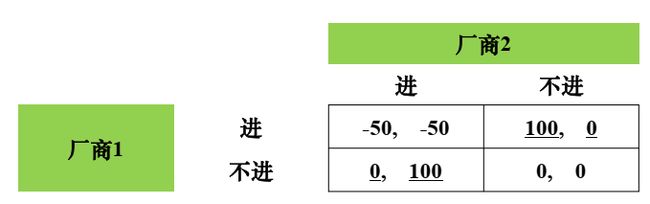
最终双方各以(2/3, 1/3)的概率选择进与不进，两者期望收益均为0

2.4.3 混合策略和严格下策反复消去法

采用混合策略时，关于严格下策反复消去法的结论仍是成立的：

• 不管是纯策略还是混合策略， 任何博弈方都不会采用任何严格下策
• 不管是纯策略纳什均衡还是混合策略纳什均衡， 严格下策反复消去法不会消去任何纳什均衡
• 若反复消去严格下策后，留下的策略组合是唯一的，那么该策略组合一定是纳什均衡

引进混合策略还能让严格下策反复消去法的用处更大：

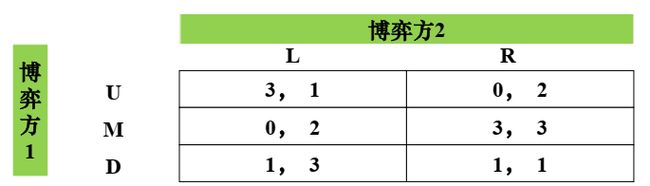
相对于混合策略(1/2, 1/2, 0)而言， D是博弈方1 的严格下策，消去后变成下图这样，之后博弈方2消去他的严格下策L，博弈方1再消去U，就达到平衡

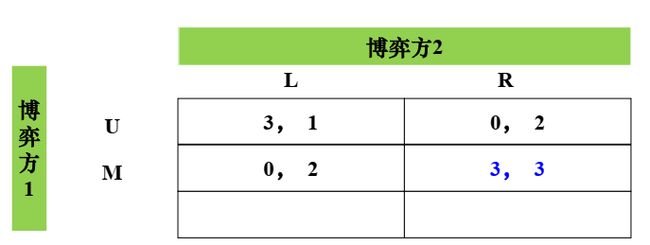
2.4.4 混合策略反应函数

混合策略反应函数：一博弈方选择策略的概率分布对另一博弈方选择策略的概率分布的反应构成的函数，反映概率分布间的函数关系。

对于猜硬币问题：

• 假设：
  盖硬币方的混合策略 $(r,1-r)$；猜硬币方的混合策略 $(q,1-q)$

• 盖硬币方的期望得益：
  $U_盖（r, q)= -1× r× q+1 × r× (1-q)+1× (1-r) × q+(-1)× (1-r) × (1-q) = -2r (2q-1)+(2q-1) $

• 盖硬币方的反应函数：

  ① 猜方猜正面的概率q<1/2时,盖方应盖正面， r=1；
  ② q>1/2，盖方应选反面，1-r=1即 r=0;
  ③ q=1/2，盖方r在[0,1]随机选。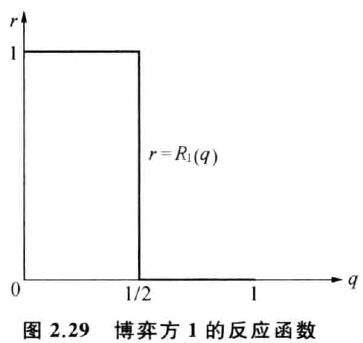

  

• 猜硬币方的反应函数 (同理可得)

  此时纵轴是自变量，横轴是因变量

  

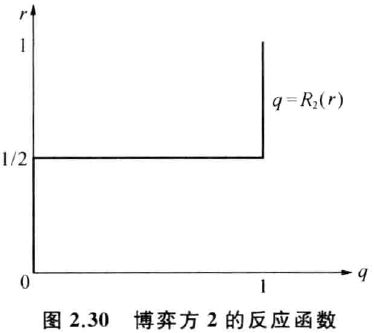
• 双方的反应函数

  

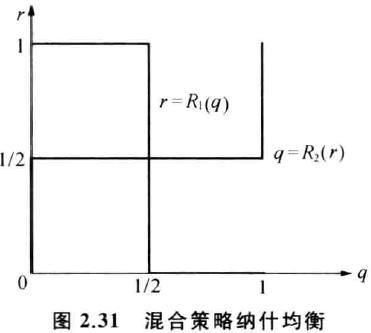
唯一交点 $(r=1/2，q=1/2)$是相互对对方最佳反应的混合策略概率分布

先写出期望得益，然后假设另一方选择的概率，判断自己的得益最大值

2.5 纳什均衡的存在性

在一个有$n$个博弈方的博弈$G=(S_1,...,S_n;U_1,...,U_n)$中,如果$n$是有限的，且 $S_i $都是有限集 ( 对i=1, …, n)，则该博弈至少存在一个纯策略纳什均衡或混合策略纳什均衡。

通俗表述：每个有限博弈都至少有一个混合策略纳什均衡。

最重要的扩展：将纳什定理从有限博弈，推广到行为或策略不可数且具有连续得益函数的无限博弈。

2.6 纳什均衡的选择和分析方法扩展

2.6.1 帕累托上策均衡和风险上策均衡

混合策略本身不一定比纯策略更好（夫妻之争），混合策略对于确定哪个纯策略更好也没有作用，由此引出了帕累托上策均衡。

在一个有多重纳什均衡的博弈中，某个纳什均衡给所有博弈方带来的得益都大于其他纳什均衡，这种纳什均衡关系就是帕累托优劣关系，依据帕累托优劣关系选择出来的纳什均衡，称为“帕累托上策均衡”。

例如在战争与和平的例子中：

纯策略纳什均衡： (战争, 战争)， (和平, 和平)，其中帕累托上策均衡： (和平, 和平)

BUT 选择和平会有更大风险，选择战争反而相对安全。从风险的角度考虑：理性的决策者不一定选择帕累托上策,由此引出风险上策博弈。

猎鹿博弈：

① 帕累托上策均衡： (鹿, 鹿)
② 选择帕累托上策均衡存在风险
A. 若猎人1抓鹿时，猎人2去抓兔，猎人1会一无所获;
B. 即使猎人2只有50%的可能性抓兔，猎人1抓鹿的期望得益5 × 0.5+0× 0.5=2.5 < 3
若考虑风险， (鹿, 鹿)不再是必然的选择。

风险上策均衡： (兔, 兔)

判别标准：若所有博弈方预计其他博弃方采用各个纳什均衡策略的概率相同时，都偏爱其中一个风险更小的纳什均衡，则该纳什均衡就是风险上策均衡。

风险上策均衡选择的自我强化机制：所有博弈方对其他博弈方可能采用风险上策均衡策略的担心，会演变为趋向都选择风险上策均衡的强烈趋势。

2.6.2 聚点均衡和相关均衡

1. 聚点均衡

   • 报时博弈：

     两博弈方同时播报时间，所报时间相同各奖100元，所报时间不同没有奖励。

     ——所有博弈方都可能大概率选择的一些特殊策略。（比如说某些整点）

   • 城市博弈

     两博弃方分别将（上海、南京、长春、哈尔滨） 4个城市分为2组，每组2个城市

     根据地域特征，人们一般会分（上海、南京），（长春、哈尔滨）

   是纳什均衡，同时是多重纳什均衡中比较容易被选择的纳什均衡。

   聚点均衡反映出：人们在多重纳什均衡选择中的某些规律性。
   聚点均衡的依据：文化、习惯、典型特征

2. 相关均衡

   在具有多重纳什均衡的博弈中，博弈双方根据相关机制选择最优策略而构成的纳什均衡，称为“相关均衡”。

   

   各均衡都不理想
   A. 两纯策略纳什均衡：双方得益相差很大，很难达成一致。
   B. 混合策略纳什均衡：有1/4的概率遇到 (U,R)

   解决办法：

   抛硬币决定：正面——(U, L)，反面——(D, R) $⟶$双方期望得益都是3，大于混合策略纳什均衡的期望得益2.5,这种机制下的纳什均衡就是相关均衡。

   更好的选择（考虑到（DL）的总得益更高）

   发出“相关信号”装置：
   (a) 以相同概率(1/3)随机发A、 B、 C三信号；
   (b) 博弈方1只能看到信号是否A，博弃方2只能看到信号是否C；
   © 博弃方1看到信号A采用U，否则采用D；博弈方2看到信号C采用R，否则采用L

   因此信号A——（U,L)，信号B——（D,L)，信号C——（D,R)，此时双方期望的益$\frac{10}{3}$

2.6.3 防共谋均衡

此时纯策略纳什均衡： (U,L,A)， (D,R,B)，其中(U,L,A)——帕累托上策。

BUT博弈方3选A，博弈方1和博弈方2共谋，分别选D和R,得益大于(U,L,A)时的得益0

防共谋均衡：

若一博弈的某个策略组合满足下列要求:

① 任何博弈方单独改变策略均不会改变博弈结果；
② 任何两个博弈方的串通也不会改变博弈结果;
③ 以次类推，直到所有博弈方都参加的串通都不会改变博弈结果。

博弈方3考虑到博弈方1和2可能共谋——》 选B，此时防共谋均衡： (D, R, B)

原因：个人、两人、 3人偏离，都不能增加利益。 ——》(D,R,B)比(U,L,A) 更稳定

启示： (D,R,B)在帕累托效率上比(U,L,A)差——》 揭示了多人博弃中更复杂的“囚徒的困境”。

Summary

此部分用于对所学内容的快速梳理记忆

1. 分析方法：上策均衡（上策是无论对方怎么选，自己的选择都是最好的）、严格下策消去法（反复消去严格下策）、划线法（针对对方的某种选择，在自己的得益最高的选择下划线）、箭头法（对每一种得益情况找往外的箭头，无往外箭头说明稳定）

2. 纳什均衡：定义（直观和数学两个）、与严格下策反复消去法的关系（不会消去纳什均衡）

3. 无限策略博弈：古诺模型求导计算及其反应函数（产量博弈$U_1=P{Q}_1-C_1{Q}_1=(8-Q)Q_1-2Q_1=6Q_1-Q_1{Q}_2-Q_1^2$）、伯特兰德寡头竞价（双方在价格上博弈，生产产品有一定替代性）、公共资源博弈（类似于古诺博弈，只是说明情况不同）、反应函数讨论（可能非连续、不可导，可能无交点无法找均衡）

4. 混合策略及其纳什均衡：

   • 基本概念（无纯策略纳什均衡时让对方无机可趁），主要是小偷和守卫博弈以及其中的激励悖论
   • 有多个纯策略纳什均衡时该怎么选，仍是用混合策略让对方无机可趁
   • 与严格下策消去的关系，某一方的纯策略可能是其他混合策略下的严格下策，可以消去
   • 反应函数：假设另一方选择的概率，判断自己的得益最大值

5. 纳什均衡存在性：每个有限博弈都至少有一个混合策略纳什均衡。

6. 纳什均衡拓展分析方法

   • 在一个有多重纳什均衡的博弈中，某个纳什均衡给所有博弈方带来的得益都大于其他纳什均衡，这种纳什均衡关系就是帕累托优劣关系，依据帕累托优劣关系选择出来的纳什均衡，称为“帕累托上策均衡”。

   • 若所有博弈方预计其他博弃方采用各个纳什均衡策略的概率相同时（50%），都偏爱其中一个风险更小的纳什均衡，则该纳什均衡就是风险上策均衡。

   • 聚点均衡：超越博弈利益关系，根据共同文化背景互相迁就，例如报时博弈：两博弈方同时播报时间，所报时间相同各奖100元，所报时间不同没有奖励

   • 相关均衡：在现实中, 当人们反复遇到相似的选择难题时, 很有可能会通过反复试探、培养默契等,形成特定的机制(制度安排)来摆脱困境。一般是通过某种外在的概率机制来进行选择，让非纳什均衡的双方都收益较好的概率更高

   • 防共谋均衡：任何博弈方单独改变策略均不会改变博弈结果，任何两个博弈方的串通也不会改变博弈结果。

All in all：找纳什均衡的方法及找混合策略的方法，还有拓展分析的方法