江的福从零开始刷算法(递归回溯--二维小结)
LeetCode 79、单词搜索

首先我们需要了解在本题中,每个点都可以作为起始点,即我们需要一个二层循环,来遍历每一个点,用这个起始点去走它的路线,判断是否可以达到题目要求。
大体结构其实还是跟在一维的递归回溯一致的,
有几点需要注意:
1、在递归中,每次需要去当前点的上下左右四个点进行判断,因此我们可以用一个数组
![]()
来对这个过程进行优化。
2、在优化的基础上,需要判断新得到的点的是否在二维平面中,

3、在以最起始那个点开始的一次查找中,所有的点不能够重复判断,因此定义一个二维的Boolean数组对应board,记录在当前查找中是否判断过该点。
并且需要在回溯的过程中将该值置为初值。
4、递归结束条件,当判断到最后一个点时,如果这个点判断成功,即可以找到。否则不能。
下面是全部代码:
class Solution {
int[][] move={{0,-1},{-1,0},{0,1},{1,0}};
boolean[][] ismoved;
public boolean exist(char[][] board, String word) {
if((board.length*board[0].length)<word.length()||board.length==0||word.length()==0){
return false;
}
ismoved=new boolean[board.length][board[0].length];
for(int i=0;i<board.length;i++){
for(int j =0;j<board[i].length;j++){
if(searchword(board,word,i,j,0)){
return true;
}
}
}
return false;
}
public boolean searchword(char[][] board,String word,int satrtx,int starty,int index){
if(index==word.length()-1){
if(word.charAt(index)==board[satrtx][starty]){
return true;
}
return false;
}
if(word.charAt(index)==board[satrtx][starty]){
ismoved[satrtx][starty]=true;
for(int i =0;i<4;i++){
int newx =satrtx+move[i][0];
int newy =starty+move[i][1];
if(isValid(newx,newy,board)&&!ismoved[newx][newy]){
if(searchword(board,word,newx,newy,index+1))
return true;
}
}
ismoved[satrtx][starty]=false;
}
return false;
}
public boolean isValid(int satrtx,int starty,char[][] board){
if(satrtx>=0&&satrtx<board.length&&starty>=0&&starty<board[0].length){
return true;
}
return false;
}
}
LeetCode 200、岛屿数量

依旧是二维的递归回溯,这种问题也叫floodfill问题。
类似于上面的题,我们只需要将等于‘1’的点,设置为起始点,开始进行查找,将同样为1 的点,在递归的过程中设置置为已经找过的点。所以设置起始点的时候,我们就需要设置它等于‘1’,并且没有被遍历过。
在递归函数中不需要对其设置结束条件,因为它只需要递归所有的点即可,条件隐藏在是否等于‘1’,和是否已经被遍历过,还有是否是有效的点。
在每次有效的最起始时,对数量进行加一。
class Solution {
boolean[][] isvalid;
int[][] move ={{-1,0},{0,-1},{1,0},{0,1}};
int m,n;
int sum=0;
public int numIslands(char[][] grid) {
m=grid.length;
if(m==0) return 0;
n=grid[0].length;
isvalid=new boolean[m][n];
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]=='1'&&!isvalid[i][j]){
isvalid[i][j]=true;
sum++;
floodfill(grid,i,j);
}
}
}
return sum;
}
public void floodfill(char[][] grid,int startx,int starty){
for(int i=0;i<4;i++){
int newx =startx+move[i][0];
int newy =starty+move[i][1];
if(ismoved(newx,newy)&&!isvalid[newx][newy]&&grid[newx][newy]=='1'){
isvalid[newx][newy]=true;
floodfill(grid,newx,newy);
}
}
}
public boolean ismoved(int startx,int starty){
if(startx>=0&&startx<m&&starty>=0&&starty<n){
return true;
}
return false;
}
}
LeetCode 130、被围绕的区域

依旧是套框架,但是我下面说的这种应该是比较笨比的办法。
这其实跟上面那个题很相似的。
我采用的办法是,题目中说‘X’必须将‘O’围绕,那么我从边界上开始找一遍‘O’,并将它是否遍历过置为true。然后再从边界中,去执行另一个加上更改值的递归方法,即可,因为第一次就将不满足的O找到并且置为了ture。下次遍不会再去找。
class Solution {
boolean[][] isvalid;
int[][] move ={{-1,0},{0,-1},{1,0},{0,1}};
int m,n;
public void solve(char[][] board) {
m=board.length;
if(board.length==0) return;
n=board[0].length;
isvalid=new boolean[m][n];
for(int i=1;i<m-1;i++){
if(board[i][0]=='O'&&!isvalid[i][0]){
isvalid[i][0]=true;
floodfill(board,i,0);
}
}
for(int i=1;i<m-1;i++){
if(board[i][n-1]=='O'&&!isvalid[i][n-1]){
isvalid[i][n-1]=true;
floodfill(board,i,n-1);
}
}
for(int j=0;j<n;j++){
if(board[0][j]=='O'&&!isvalid[0][j]){
isvalid[0][j]=true;
floodfill(board,0,j);
}
}
for(int j=0;j<n;j++){
if(board[m-1][j]=='O'&&!isvalid[m-1][j]){
isvalid[m-1][j]=true;
floodfill(board,m-1,j);
}
}
for(int i=1;i<m-1;i++){
for(int j=1;j<n-1;j++){
if(board[i][j]=='O'&&!isvalid[i][j]){
isvalid[i][j]=true;
board[i][j]='X';
floodfill1(board,i,j);
}
}
}
}
public void floodfill(char[][] grid,int startx,int starty){
for(int i=0;i<4;i++){
int newx =startx+move[i][0];
int newy =starty+move[i][1];
if(ismoved(newx,newy)&&!isvalid[newx][newy]&&grid[newx][newy]=='O'){
isvalid[newx][newy]=true;
floodfill(grid,newx,newy);
}
}
}
public void floodfill1(char[][] grid,int startx,int starty){
for(int i=0;i<4;i++){
int newx =startx+move[i][0];
int newy =starty+move[i][1];
if(ismoved(newx,newy)&&!isvalid[newx][newy]&&grid[newx][newy]=='O'){
isvalid[newx][newy]=true;
grid[newx][newy]='X';
floodfill1(grid,newx,newy);
}
}
}
public boolean ismoved(int startx,int starty){
if(startx>=0&&startx<m&&starty>=0&&starty<n){
return true;
}
return false;
}
}
LeetCode 417 、太平洋大西洋水流问题
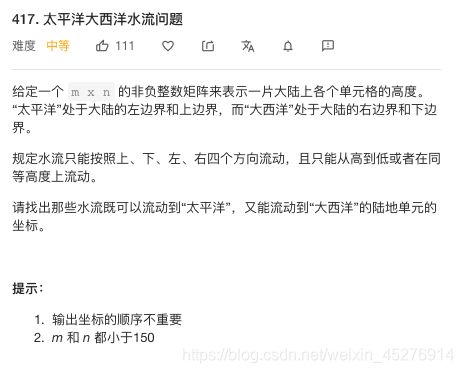

我这种方法依旧是笨比方法。
想对它进行优化的,但不曾想优化失败了,希望看见的大佬们也能帮我看看。
大致的过程和上面都差不多,注意的是新点要等于或小于上一个点的值。
我的笨比办法的主要思想是:一个点必须满足能到太平洋也能到大西洋,那就用两个递归函数,分别判断,是否该点既能到太平洋也能到大西洋。若都为true,将该点存入res中。
class Solution {
int m,n;
boolean[][] falgs ;//判断是否走过
boolean[][] isvalidp;//存每个这个点是否能到太平洋
boolean[][] isvalida;//寻每个点是否能到大西洋
boolean[][] novalidp;//存一定不能到太平洋的点
boolean[][] novalida;//一定不能到大西洋
int[][] move={{-1,0},{1,0},{0,-1},{0,1}};
List<List<Integer>> res =new ArrayList<>();
public List<List<Integer>> pacificAtlantic(int[][] matrix) {
m = matrix.length;
if(m==0) return res;
n =matrix[0].length;
falgs =new boolean[m][n];
isvalidp =new boolean[m][n];
isvalida=new boolean[m][n];
novalidp=new boolean[m][n];
novalida=new boolean[m][n];
List<Integer> list1;
for(int i=0;i<m;i++){
for(int j =0;j<n;j++){
falgs[i][j]=true;
List<Integer> list =new ArrayList<>();
if(gogogop(matrix,i,j,m,n)&&gogogoa(matrix,i,j,m,n)){
list.add(i);
list.add(j);
list1 =new ArrayList<>();
list1.addAll(list);
res.add(list1);
isvalidp[i][j]=true;
isvalida[i][j]=true;
}
falgs[i][j]=false;
}
}
return res;
}
public boolean gogogop(int[][] matrix,int startx,int starty,int m,int n){
if(startx==0||starty==0) return true;
if(isvalidp[startx][starty]) return true;
//if(novalidp[startx][starty]) return false;
for(int i =0;i<4;i++){
int newx =startx+move[i][0];
int newy =starty+move[i][1];
if(isvalided(newx,newy)&&!falgs[newx][newy]&&matrix[newx][newy]<=matrix[startx][starty]){ falgs[newx][newy]=true;
if(gogogop(matrix,newx,newy,m,n)){
falgs[newx][newy]=false;
isvalidp[newx][newy]=true;
return true;
}
falgs[newx][newy]=false;
}
}
//novalidp[startx][starty]=true;
return false;
}
public boolean gogogoa(int[][] matrix,int startx,int starty,int m,int n){
if(startx==m-1||starty==n-1) return true;
if(isvalida[startx][starty]) return true;
// if(novalida[startx][starty]) return false;
for(int i =0;i<4;i++){
int newx =startx+move[i][0];
int newy =starty+move[i][1];
if(isvalided(newx,newy)&&!falgs[newx][newy]&&matrix[newx][newy]<=matrix[startx][starty]){ falgs[newx][newy]=true;
if(gogogoa(matrix,newx,newy,m,n)){
falgs[newx][newy]=false;
isvalida[newx][newy]=true;
return true;
}
falgs[newx][newy]=false;
}
}
//novalida[startx][starty]=true;
return false;
}
public boolean isvalided(int startx,int starty){
if(startx>=0&&startx<m&&starty>=0&&starty<n){
return true;
}
return false;
}
}
就先写这么多吧。继续学习了。
中国加油。