【PAT甲级】2022冬季-PAT甲级AK题解

这是本人第一次尝试去写博客，可能会有一些不足的地方。

第一次接触PTA是在2022年的天梯赛，当时为了能拿一个不错的分数，刷了天梯赛题库里面所有5-25分题目，可惜最后只有151分没有能拿到个人奖项，只有一个团队三等奖。之后看到PTA平台有一个PAT考试就尝试了解了一下，在CSDN上大佬们都说这个考试可以在部分院校的复试中抵机试分就尝试报名了，2022夏季乙级AK，2022秋季甲级没报上（以为报上了其实没交钱，后来去教育超市里面买了真题卷也AK了），2022冬季甲级2小时30分钟有惊无险AK。下面开始上题目。

一. Reduction of Proper Fractions

A Proper Fraction（真分数）is a fraction where the numerator（分子）is less than the denominator（分母）. To reduce a fraction, we are supposed to cross out any common factors between the numerator and the denominator.

Here is another way to do the reduction: simply cross out any common digits. In most of the cases, this way cannot give the correct result. However, sometimes it happends to work! For example: 26/65 = 2/5 where 6 is crossed out.

Now given a proper fraction, you are supposed to tell if this simple reduction works or not.

Input Specification:

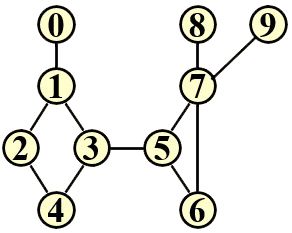
Each input file contains one test case, with the numerator a and the denominator b of the proper fraction given in a line, separated by a space. It is guaranteed that 0

Output Specification:

For each test case, print in a line both fractions before and after the simple reduction. If they are equal, put a = between them; else put != instead. The format is either a/b = c/d or a/b != c/d.

Sample Input 1:

39 195

Sample Output 1:

39/195 = 3/15

算法标签: 字符串 模拟

题意解读: 将一个真分数（输入）进行化简以一种简单划掉相同数字的方式，同时也将这个真分数进行真正的化简，最后比较两者化简结果是否相同。

简要思路: 对于划掉化简需要将a和b当做字符串来进行处理，使用一个新的空字符串来作为划掉后的a和b，通过对原始a和b进行遍历来得到划掉后的a和b。对于真正的化简，由于此处其实并不重点考察该内容，对于(0,10^5]我们完全可以使用最为暴力的方式循环遍历i∈[2,min(a,b)]，如果a和b都可以整除i，那就进行一次化简同时再次遍历该过程，直至没有任何一个i可以被a和b整除，此时说明化简完毕。最后比较两者化简结果即可。

坑点详解

1. 在划掉相同数字的时候需要一一对应消除，举个例子a=2211 b=21341 此时a中有两个数字2和两个数字1，b中有一个数字2和两个数字1，那么对于b我们当然可以把2和1全部划掉，但是对于a我们只能划掉一个数字2和两个数字1，最后a=1 b=34。（这个坑点也是导致我一直通不过此题的原因，我把a中的2和1全部划掉了）

2. （这是一个可能的坑点，没有进行测试）如果a或b被全部划掉了，那么其实a或b应该为0，当然由于a

AC代码（由于当时未想到坑点1,所以可能进行了很多没有必要的排坑步骤,即数字、字符串互转）:

#include
#include
using namespace std;
int booka[100];
int bookb[100];
int main(){
	string a,b;
	cin>>a>>b;
	string ansa="";
	string ansb="";
	for(int i=0;i

二. Luggage Pickup

When a flight arrives, the passengers will go to the Arrivals area to pick up their baggage from a luggage conveyor belt （行李传送带）.

Now assume that we have a special airport that has only one pickup window for each conveyor belt. The passengers are asked to line up to pick up their luggage one by one at the window. But if one arrives at the window yet finds out that one is not the owner of that luggage, one will have to move to the end of the queue and wait for the next turn. At the mean time, the luggage at the window will wait until its owner picks it up. Suppose that each turn takes 1 minute, your job is to calculate the total time taken to clear the conveyor belt, and the average waiting time for the passengers.

For example, assume that luggage i belongs to passenger i. If the luggage come in order 1, 2, 3, and the passengers come in order 2, 1, 3. Luggage 1 will wait for 2 minutes to be picked up by passenger 1. Then the luggage queue contains 2 and 3, and the passenger queue contains 3 and 2. So luggage 2 will wait for 2 minutes to be picked up by passenger 2. And finally 3 is done at the 5th minute. The average waiting time for the passengers is (2+4+5)/3≈3.7.

Input Specification:

Each input file contains one test case. The first line gives a positive integer N (≤10^3). Then N numbers are given in the next line, which is a permutation of the integers in [1,N], representing the passenger queue. Here we are assuming that the luggage queue is in order of 1, 2, ..., N, and the i-th luggage belongs to passenger i.

All the numbers in a line are separated by a space.

Output Specification:

For each test case, print in a line the total time taken to clear the conveyor belt, and the average waiting time for the passengers (output 1 decimal place). The numbers must be separated by 1 space, and there must be no extra space at the beginning or the end of the line.

Sample Input:

5
3 5 1 2 4

Sample Output:

9 6.0

算法标签：队列 模拟

题意解读：给到两个序列，即行李序列和乘客序列，乘客序列由输入给出、行李序列为[1,2,...,N]。当乘客与行李匹配时，乘客拿走行李，行李序列向后遍历，乘客序列向后遍历；当乘客与行李不匹配时，行李序列不变，该乘客移动至序列尾。直至行李序列和乘客序列为空。

简要思路：N<=10^3说明这道题怎么暴力怎么来，我们用vector代替queue，根据输入构造出乘客vector，然后定义一个行李index用来标记此时行李编号，主循环单层遍历乘客vector，如果匹配则行李index++，若不匹配则乘客vector.push_back(当前乘客)，直至行李index==N+1则说明遍历完成。

坑点详解：

1. 计算平均等待时间时，每个乘客都是从0开始等待的，因此当一位乘客成功拿到行李时总等待时间+=当前时间。

AC代码：

#include
#include
using namespace std;
int main(){
	int n;
	cin>>n;
	vector  A;
	for(int i=0;i>a;
		A.push_back(a);
	}
	int allneed=0;
	int huowu=1;
	int shijian=1;
	int i;
	for(i=0;;i++){
		if(A[i]==huowu){
			allneed+=shijian;
			huowu++;
			if(huowu==n+1) break;
		}
		else  A.push_back(A[i]);
		shijian++;
	}
	printf("%d %.1f",shijian,(float)allneed/n); 
}

三. Articulation Points

In graph theory, given a connected graph G, the vertices whose removal would disconnect G are known as articulation points. For example, vertices 1, 3, 5, and 7 are the articulation points in the graph shown by the above figure (also given by the sample input).

It is a bit complicated to find the articulation points. Here you are only asked to check if a given vertex is an articulation point or not.

Input Specification:

Each input file contains one test case. For each case, the first line contains 3 positive integers: N (≤10^3), M (≤10^4), and K (≤100), which are the number of vertices, the number of edges, and the number of queries, respectively. Then M lines follow, each gives an undirected edge in the format:

v1 v2

where v1 and v2 are the two ends of an edge. Here we assume that all the vertices are numbered from 0 to N−1. It is guaranteed that v1 is never the same as v2, and the graph is connected.

Finally a line of queries are given, which contains K vertices to be checked. The numbers in a line are separated by spaces.

Output Specification:

Output a string of 0's and 1's in a line. That is, for each query, print 1 if the given vertex is an articulation point, or 0 if not. There must be no space between the answers.

Sample Input:

10 11 8
0 1
8 7
9 7
1 2
1 3
3 5
5 7
2 4
3 4
5 6
6 7
5 2 9 1 6 3 2 7

Sample Output:

10010101

算法标签：并查集

题意解读：给定一个无向连通图，问你在该无向图中某个点是否是Articulation Point，即如果去掉该点，其余点所组成的图是否仍为一个连通图，即连通块个数是否仍为1

简要思路：使用一个vector记录所有的边，对于每一次询问，将不以该点为端点的边的两个端点进行并查集merge/union，最后遍历其余点的并查集father/root，如果该点与其father/root值相同，则说明连通块数量+1，最后判断连通块数量是否>=2。

坑点详解：

1. 对于每一次询问，都需要重置father/root数组，不然前面的询问会对后面的询问造成影响。

2. 在进行merge/union和最后的find时，不要考虑询问的那个点，因为题意就是如果去掉这个点之后的情况。

AC代码：

#include
#include
#include
using namespace std;
vector  >edge;
int father[1005];
int find(int a){
	if(father[a]==a) return a;
	return father[a]=find(father[a]);
}
void union1(int a,int b){
	int root1=find(a);
	int root2=find(b);
	if(root1!=root2) father[root1]=root2;
}
int main(){
	int n,m,k;
	cin>>n>>m>>k;
	for(int i=0;i>a>>b;
		edge.push_back({a,b});
	}
	string ans="";
	for(int i=0;i>a;
		for(int j=0;j p=edge[j];
			if(p.first==a||p.second==a) continue;
			//cout<=2){
				ans+='1';
				goto end;
			}
		}
		ans+='0';
		end:;
		//cout<

四. Check Inorder Traversals

Suppose that all the keys in a binary tree are distinct positive integers. A unique binary tree can be determined by a given pair of postorder and inorder traversal sequences, or preorder and inorder traversal sequences. However, if only the postorder and preorder traversal sequences are given, the corresponding tree may no longer be unique.

Now given a pair of postorder and preorder traversal sequences, you are supposed to check a set of inorder traversal sequences, and answer whether or not they are indeed inorder traversal sequences of the tree.

Input Specification:

Each input file contains one test case. For each case, the first line gives a positive integer N (≤ 30), the total number of nodes in the binary tree. The second line gives the preorder sequence and the third line gives the postorder sequence.

Then another positive integer K (≤ 10) is given, followed by K lines of inorder traversal sequences.

Each sequence consists of N positive integers. All the numbers in a line are separated by a space.

Output Specification:

For each inorder traversal sequence, print in a line Yes if it is an inorder traversal sequence of the tree, or No if not.

On the other hand, there is another possible case that the given pre- and postorder traversal sequences can NOT form any tree at all. In that case, first print in a line Are you kidding me?. Then for each inorder traversal sequence of the input, try to construct a tree with the given preorder traversal sequence, and output in a line the correct postorder traversal sequence. If it is still impossible, output You must be kidding me! instead.

Sample Input 1:

4
1 2 3 4
2 4 3 1
4
2 1 3 4
1 2 3 4
2 1 4 3
2 1 5 6

Sample Output 1:

Yes
No
Yes
No

Sample Input 2:

7
1 2 3 4 6 7 5
6 7 5 4 3 2 1
3
2 1 6 4 7 3 5
2 1 6 7 4 3 5
2 3 1 7 4 5 6

Sample Output 2:

Are you kidding me?
2 6 7 4 5 3 1
2 7 6 4 5 3 1
You must be kidding me!

算法标签: 朴素二叉树

题意解读: 

给定一个前序遍历和后序遍历，你首先需要判断其是否可能构成一颗二叉树。

如果可以构成，那么对于给定的中序遍历序列，你需要判断其是否是该二叉树的可能中序遍历。

如果不可以构成，那么对于给定的中序遍历序列，你需要判断其与前序遍历序列能否构成一颗二叉树，如果可以则输出构成的二叉树的后序遍历，如果不可以则输出对应字符串。

详细思路:

首先是判断一个前序遍历和后序遍历是否可能构成一颗二叉树。如下例

前序遍历1 2 3 4 5 6

后序遍历3 4 2 6 5 1

前序遍历就是根左右，后序遍历是左右根。因此对于前序遍历而言，其第一个值（下标为0）1便是此时结点的值，而其第二个值（下标为1）2便是左孩子结点的值，若其没有左孩子则为右孩子结点的值。

怎么判断到底有没有左孩子呢？此时就需要后序遍历，其是左右根，对于左孩子结点的值应该出现在后序遍历的左边，对于样例而言其出现在了后序遍历下标为2的位置，因此可以判断后序遍历中的3 4 2是左子树的后序遍历，则剩余部分6 5便是右子树的后序遍历。由于前序遍历和后序遍历的长度一定相同，因此左子树的前序遍历为2 3 4，右子树的后序遍历为5 6。按照此方式便可以递归划分左右子树，以此建树。

那么问题来了，题目是问我（读者）是否可能构成一颗二叉树，按照你（博主）的逻辑好像其一定可以建成啊。那么好，我们此时以样例二来进行以上过程，来判断其为什么不能建成树。如下例

前序遍历1 2 3 4 6 7 5

后序遍历6 7 5 4 3 2 1

首先前序遍历第一个值1为根节点的值，第二个值2为左孩子结点的值，然后在后序遍历中寻找2的位置，发现其在最后一个（1是根节点的值不参与判断），但是按照左右根的顺序，最后一个不应该是右孩子结点的值吗？此时发生了这样一种情况，这个结点没有左孩子或右孩子，那么此时它是左孩子或右孩子都可以（这不是能否建成树的原因），因此我们默认其为左孩子。那么得到如下划分，其中右子树为空故不列举。

前序遍历2 3 4 6 7 5

后序遍历6 7 5 4 3 2

再次划分

3 4 6 7 5

6 7 5 4 3

再次划分

4 6 7 5

6 7 5 4

此时前序遍历中的第二个值6出现在后序遍历的最左边，因此6即为左结点的值，且其没有左右子树，即这个6是一个叶子结点。那么剩下的就是右子树的内容，如下

前序遍历7 5

后序遍历7 5

此时就来到了一种很奇怪的情况，前序遍历的第一个和后序遍历的最后一个不相同，这就是无法构成二叉树的主要原因！！！。还有一个原因在坑点详解中描述。

哈哈哈此时我只是知道了给定的前序遍历和后序遍历能否构成二叉树，我还不知道怎么判断对于查询的中序遍历是否可以由构成的二叉树中序遍历得到。

此时我的逻辑是：如果一个前序遍历和后序遍历构成的可能的二叉树，可以（假设）得到查询的中序遍历，那么我用前序遍历和查询的中序遍历构成的唯一的二叉树就一定可以得到后序遍历；反之如果得不到那么这个中序遍历是不可行的。

坑点详解:

1. 无法建成树的第二个原因，仔细观察样例其实可以发现，对于样例1的第4个查询，其中出现了一个不可能的值6，那么如果你按照这个6去建树，在find的过程中是不可能找到这个6的，因此第二个原因是，在find的过程中无法找到值。正常来讲是绝对可以找到的。

AC代码:

#include
#include
#include
using namespace std;
struct node{
	int data;
	node* l;
	node* r;
};
int find(int a,int post[],int length){
	for(int i=0;idata=pre[0];
	p->l=NULL;
	p->r=NULL;
	int site=find(pre[0],in,length);
	if(site==length){
		flag1=1;
		return p;
	} 
	p->l=qzbuild(pre+1,in,site);
	p->r=qzbuild(pre+site+1,in+site+1,length-site-1);
	return p;
}
vector  ans;
void postorder(node* root){
	if(root!=NULL){
		postorder(root->l);
		postorder(root->r);
		ans.push_back(root->data);
	}
}
int main(){
	int n;
	cin>>n;
	int pre[35];
	int post[35];
	for(int i=0;i>pre[i];
	for(int i=0;i>post[i];
	build(pre,post,n);
	int k;
	cin>>k;
	if(flag){
		cout<<"Are you kidding me?"<>in[j];
			node* root=qzbuild(pre,in,n);
			if(flag1){
				cout<<"You must be kidding me!"<>in[j];
			node* root=qzbuild(pre,in,n);
			if(flag1){
				cout<<"No"<