CSP-J P1 分糖果(洛谷P7909)
题目传送门:[CSP-J 2021] 分糖果(民间数据) - 洛谷
提示:以下是本篇文章正文内容,下面案例可供参考
复赛爆炸……
一、题目:
题目背景
红太阳幼儿园的小朋友们开始分糖果啦!
题目描述
红太阳幼儿园有 nn 个小朋友,你是其中之一。保证 n \ge 2n≥2。
有一天你在幼儿园的后花园里发现无穷多颗糖果,你打算拿一些糖果回去分给幼儿园的小朋友们。
由于你只是个平平无奇的幼儿园小朋友,所以你的体力有限,至多只能拿 RR 块糖回去。
但是拿的太少不够分的,所以你至少要拿 LL 块糖回去。保证 n \le L \le Rn≤L≤R。
也就是说,如果你拿了 kk 块糖,那么你需要保证 L \le k \le RL≤k≤R。
如果你拿了 kk 块糖,你将把这 kk 块糖放到篮子里,并要求大家按照如下方案分糖果:只要篮子里有不少于 nn 块糖果,幼儿园的所有 nn 个小朋友(包括你自己)都从篮子中拿走恰好一块糖,直到篮子里的糖数量少于 nn 块。此时篮子里剩余的糖果均归你所有——这些糖果是作为你搬糖果的奖励。
作为幼儿园高质量小朋友,你希望让作为你搬糖果的奖励的糖果数量(而不是你最后获得的总糖果数量!)尽可能多;因此你需要写一个程序,依次输入 n, L, Rn,L,R,并输出出你最多能获得多少作为你搬糖果的奖励的糖果数量。
输入格式
输入一行,包含三个正整数 n, L, Rn,L,R,分别表示小朋友的个数、糖果数量的下界和上界。
输出格式
输出一行一个整数,表示你最多能获得的作为你搬糖果的奖励的糖果数量。
输入输出样例
输入 #1复制
7 16 23
输出 #1复制
6
输入 #2复制
10 14 18
输出 #2复制
8
输入 #3复制
见附件中的 candy/candy3.in。
输出 #3复制
见附件中的 candy/candy3.ans。
说明/提示
【样例解释 #1】
拿 k = 20块糖放入篮子里。
篮子里现在糖果数 20 >= n = 7,20≥n=7,因此所有小朋友获得一块糖;
篮子里现在糖果数变成 13 >= n = 7,13≥n=7,因此所有小朋友获得一块糖;
篮子里现在糖果数变成 6 < n = 7
容易发现,你获得的作为你搬糖果的奖励的糖果数量不可能超过 66 块(不然,篮子里的糖果数量最后仍然不少于 nn,需要继续每个小朋友拿一块),因此答案是 66。
【样例解释 #2】
容易发现,当你拿的糖数量 kk 满足 14 = L \le k \le R = 1814=L≤k≤R=18 时,所有小朋友获得一块糖后,剩下的 k - 10k−10 块糖总是作为你搬糖果的奖励的糖果数量,因此拿 k = 18k=18 块是最优解,答案是 88。
【数据范围】
| 测试点 | n \len≤ | R \leR≤ | R - L \leR−L≤ |
|---|---|---|---|
| 11 | 22 | 55 | 55 |
| 22 | 55 | 1010 | 1010 |
| 33 | {10}^3103 | {10}^3103 | {10}^3103 |
| 44 | {10}^5105 | {10}^5105 | {10}^5105 |
| 55 | {10}^3103 | {10}^9109 | 00 |
| 66 | {10}^3103 | {10}^9109 | {10}^3103 |
| 77 | {10}^5105 | {10}^9109 | {10}^5105 |
| 88 | {10}^9109 | {10}^9109 | {10}^9109 |
| 99 | {10}^9109 | {10}^9109 | {10}^9109 |
| 1010 | {10}^9109 | {10}^9109 | {10}^9109 |
对于所有数据,保证 2 \le n \le L \le R \le {10}^92≤n≤L≤R≤109。
附件下载
candy.zip847B
示例:pandas 是基于NumPy 的一种工具,该工具是为了解决数据分析任务而创建的。
二、分析
1.题意:
当k>=n时,k-=[l……r]的区间,求k
2.做法
1.不难见,for套while走人,非常粗暴的做法,复杂度较高
#include
using namespace std;
int n,l,r,ans,ma;
int main()
{
cin>>n>>l>>r;
for(int i=r;i>=l;i--)
{
int k=i;
while(k-n>0){
k-=n;
}
if(k!=n)
ans=max(ans,k);
}
cout<
2.用%……:ans=max(i%n,ans);减法翻版
3.打表找规律:以样例2为例:
输入 #2复制
10 14 18
输出 #2复制
8
k=18是最优解:18%10=8,17%10=7,16%10=6,14%10=4;
再来一组:
输入 #1复制
7 16 23
输出 #1复制
6
k=20时是最优解:20%7=6,19%6=5,18%6=4……14%7=0,13%7=6;
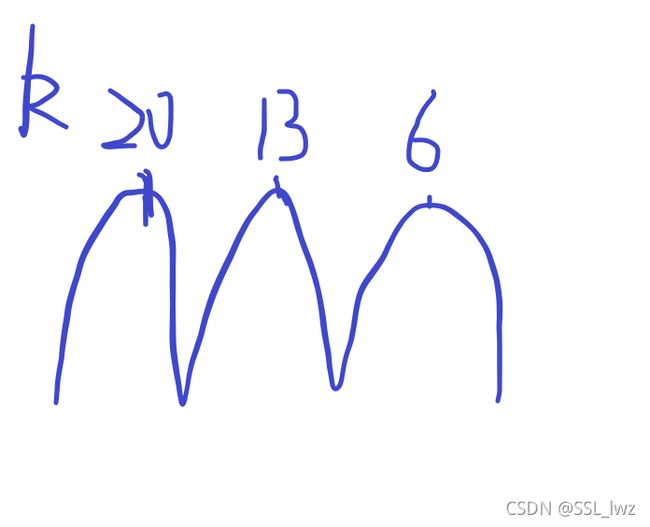
不难看出,ans是一个一个山峰,且山顶高度一样,像这样:
也就是说,ans有递增与递减两个阶段,且递减的第一个ans的顶端一定是解,像这样:
其中红色是ans,k是蓝色
正解在第一个递减处的前端:
#include
using namespace std;
long long n,l,r,ans,ma;
int main()
{
cin>>n>>l>>r;
for(int i=r;i>=l;i--){
long long k=i;
ans=max(ans,k%n);
ma=max(ans,ma);
if(ans!=ma) break;//出现递减
}
cout< 4.l/n==r/n时,说明山高度在递增,输出r%n即可
否则,输出n-1(l至r有最高山峰)
#include
using namespace std;
int n,l,r;
int main(){
cin>>n>>l>>r;
if(l/n==r/n) cout<