(搞定)排序数据结构(1)插入排序 选择排序+冒泡排序

目录

本章内容如下  

 一:插入排序              

                1.1插入排序    

              1.2希尔排序    

二：选择排序     

              2.1选择排序

 三:交换排序      

             3.1冒泡排序

---

一:插入排序                    
 

        1.1直接插入排序
    

        说到排序，其实在我们生活中非常常见，比如当我们需要在网上买东西的时候，  我们可以按照价格排序，也可以按照销量进行排序，所以对于我们来说学习排序这个数据结构是非常重要的，在本文中，我会尽可能按照我的理解将目录中的排序给将清楚。

        

                     下面就是我在一个网购网站中进行截取的图片，我们可以看到排序无处不见。

    
        
        现在让我们进入排序的讲解！！
            
            首先我们讲解的是插入排序
                首先我们来认识一下插入排序这个算法，插入排序顾名思义就是插入到前(n-1)个有序
                数中，这就像我们生活中经常玩扑克牌的时候的思想，我们玩扑克牌的时候有一种摸牌
                思路就是将第一张牌有序，然后让后面的牌进行插入使得我们的牌一直有序。
                 
                 下面我通过一群数字来进行讲解
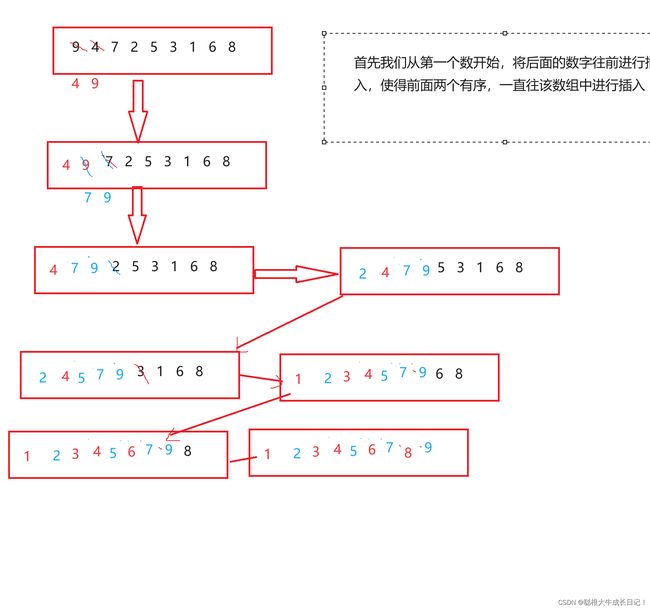
                   比如说我们的数组中的值为   9   4    7   2   5   3   1  6   8  
                     这9个数字那么我们如何使得这个数组有序呢？
                     我们通过画图来进行讲解！！

        很明显我们对于插入排序的思想

 思路 ：假设我们要插入第n个数，我们需要保证前n-1个数有序，然后再进行插入，没插入一个数我们就要将该数前面的数与要插入的数经行比较，如果大于这个要插入的数那我们就将他玩后面进行移动就可以了。
    
      
        

        

void InsertSort(int* a, int n)
{
    //使前n-1个数先有序，然后插入第n个数
    for (int  i = 0; i < n-1; i++)
    {
        int end = i;
        int tmp = a[end + 1];
        //一趟插入排序的思路
        while (end >= 0)
        {
            
            if (tmp < a[end])
            {
                a[end + 1] = a[end];
                end--;
            }
            else
            {
                break;
            }

        }
        a[end + 1] = tmp;
    }
}

        
    
            现在让我们来算一下插入排序的时间复杂度，与空间复杂度吧。
                时间复杂度最好：O(N),     最坏：O(n^2)
                首先我们不难发现它的空间复杂度为O(1)
                最坏时间复杂度:O(n^2),当一个数组为逆序的时候，就是插入排序的最坏的
                情况，在这种情况下我们一共有N个数字，插入一个数我们就需要将前面的
                数字全部像后面进行移动一次，然后在插入所以总共来说就是N*N.
                最好的情况是什么呢，最好的情况当然是当数组顺序有序的时候，每一个数
                只要插入就行了，而不需要移动元素，插入的时间复杂度为O(1),所以总共
                的时间复杂度为O(1*N)=O(N).

1.2希尔排序
    

            其实希尔排序的本质也是插入排序，希尔排序只是在插入排序上进行的一个优化的
            排序我们在上面的插入排序中不难发现，当数组有序的时候，我们的插入排序的
            时间复杂度是非常好的为O(N),而我们的希尔大佬就是看到了这个特点，
            所以就在插入排序中进行了优化，才有了我们著名的一个排序算法叫做希尔排序。
      

     希尔排序的思想是什么呢？
                其实希尔排序的思想其实也非常简单 先预排序，在直接插入排序。
                1：先对数组进行多组预排序，使得数组中的一些子数组接近有序。
                2：在对数组进行插入排序。
            我们用图来讲解一组预排序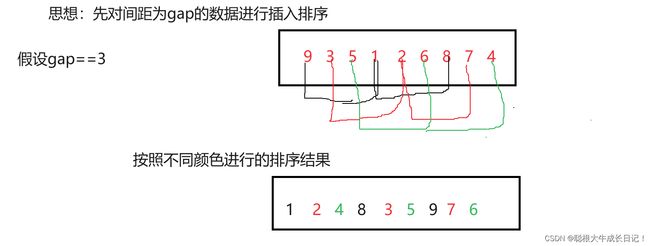

         我们不难看出在进行一组预排序完成后我们的数组相对于原来的数组就接近有序了，
         且gap越小的时候我们的数组越接近有序，当gap==1的时候我们的，我们的预排序
         就是直接插入排序。
                   代码如下：
                               

//版本一
void ShellSort(int* a, int n)
{
    int k = 0;
    int gap = n;
    while(gap!=1)
    {
        gap /= 2;//最后一次gap一定等于1
        //多组预排序，也就是我们图中红黑绿三组进行预排序
        for (int j = 0; j < gap; j++)
        {
            //一组预排序操作
            for (int i = 0; i < n - gap; i += gap)
            {
                int end = i;
                int tmp = a[end + gap];
                while (end >= 0)
                {
                    if (tmp < a[end])
                    {
                        a[end + gap] = a[end];
                        end -= gap;
                    }
                    else
                    {
                        break;
                    }
                }
                a[end + gap] = tmp;
            }
        }
    }
    
}

```

```c
```版本二：有点像优化的版本
void ShellSort(int* a, int n)
{
    int k = 0;
    int gap = n;
    while(gap!=1)
    {
        gap=gap/3 +1;//最后一次gap一定等于1    
            //间距为gap的值从前往后直接进行交换
            for (int i = 0; i < n - gap; i ++)
            {
                int end = i;
                int tmp = a[end + gap];
                while (end >= 0)
                {
                    if (tmp < a[end])
                    {
                        a[end + gap] = a[end];
                        end -= gap;
                    }
                    else
                    {
                        break;
                    }
                }
                a[end + gap] = tmp;
            }
    }
    
}
    

 

         希尔排序的时间复杂度是多少呢？
         其实书上也没有给出明确的证明，有很多种不同的看法,但是差不多是O(N^1.3)，这个我也不会证明，需要涉及到高阶的数学。
       大家如果有兴趣的话可以去证明一下。

        到这里我们的插入排序就讲解完毕了，希尔排序需要大家自行的去画图，多思考。
        
--------    

二:选择排序
    
        

其实我们的选择排序有两种，一种是直接选择排序，也是我们讲解的排序，还有一种就是堆排序，而堆排序我们之前已经讲解过了，如果你还没看的话建议先直接去补一下。

        堆排序链接：https://blog.csdn.net/2201_75964502/article/details/133017420?spm=1001.2014.3001.5501    

 在这里我们主要讲解选择排序的优化版本，就是我们遍历一边数组，选出两个值，
        一个最大值我们往后面插入，还有一个最小值玩前面插入。
        直到我们将数组排序好就可以了。
        思想：遍历一遍选最大值与最小值，然后排序就行了。
        图：这里只写了1个步骤

        代码如下：
            

void SelectSort(int* a, int n)
{
    
    int begin = 0;
    int end = n-1;
    
    while (begin < end)
    {
        int maxi = begin;
        int mini = begin;
        for(int i =begin;i<=end;i++)
        {
            //选最小的下标
            if (a[mini] > a[i])
            {
                mini = i;
            }
            //选最大的下标
            if (a[maxi] < a[i])
            {
                maxi = i;
            }
        }
        Swap(&a[begin], &a[mini]);
        //防止最大值就在begin处
        if (begin == maxi)
        {
            maxi = mini;
        }
        Swap(&a[maxi], &a[end]);

        begin++;
        end--;
    }
}

    选择排序的时间复杂度：O(^2)
          因为它的时间复杂度算法是一个等差数列：(n)+(n-2)_......+2+0
          每次都需要遍历数组选两个值，固定的        

          所以选择排序是很稳定的。

-------
三：交换排序

        
        其实我们的交换排序也有两种，一种是快速排序，另外一种就是我们本章所讲解的
        冒泡排序，而我们的快速排序由于有几种方法，且有点难，所以我会独自整理成一篇
        文章来进行讲解我们的快速排序。
        
            其实冒泡排序可能是我们见过最多的一种排序，它的思想并不难理解
            冒泡排序的思想是什么呢？
            思想：
                遍历一遍数组，两两相邻的元素进行比较，将数组中最大元素的值给冒到最
                后去，一直遍历，直到数组变成有序的数组
                
                代码如下：
                

        

void BubbleSort(int* a, int n)
{
    int i = 0;
    //一共冒泡几趟
    for (int  i = 0; i < n-1; i++)
    {
        int exchange = 1;
        //一趟内部
        for (int j = 0; j < n-i-1; j++)
        {
            if (a[j] > a[j + 1])
            {
                exchange = 0;
                Swap(&a[j], &a[j + 1]);
            }
        }
        if (exchange == 1)
        {
            //说明原数组有序,就不需要进行排序了
            break;
        }

    }

}

    冒泡排序的时间复杂度：O(N^2)
    它非常稳定。，因为时间复杂度是固定的

        感谢大家的观看，如果你觉得对你有帮助的话，可以给博主一个赞哦！！