【树上莫队C++】Count on Tree II（欧拉序降维，树链剖分求最近共同祖先LCA）

》》》算法竞赛

/**
 * @file            
 * @author          jUicE_g2R(qq:3406291309)————彬(bin-必应)
 *						一个某双流一大学通信与信息专业大二在读	
 * 
 * @brief           一直在算法竞赛学习的路上
 * 
 * @copyright       2023.9
 * @COPYRIGHT			 原创技术笔记：转载需获得博主本人同意，且需标明转载源
 *
 * @language        C++
 * @Version         1.0还在学习中  
 */

• UpData Log 2023.9.18-9.21 更新进行中
• Statement0 一起进步
• Statement1 有些描述可能不够标准，但能达其意

技术提升站点

莫队算法 就是一种优雅的 暴力法（美学）!!!

长篇大论警告！！！

19-3 树上莫队

可以学到的芝士有：欧拉序 、最近共同祖先LCA、 DFS的两种遍历方式 、树链剖分

• 基础莫队算法 与 待修改的莫队算法 操作都是 一维数组

像 树 这种二维的如果可以进行降维（将树转化成链处理）处理的话，也可以使用 莫队算法 处理。

例如： 树形结构的路径问题，可以用到 “欧拉序” 把整棵树的结点顺序换成一个一维数组处理，将路径问题变成区间问题

19-3-1 什么是 欧拉序Ora_Order？

Ora_Order 欧拉序 是 一种特殊的 DFS

• 从根节点出发，按DFS再绕回根节点

• 有两种情况：

1）在每个节点第一次进和最后一次出时加入序列。每个点都会加两遍！！！（第一次是进，第二次是出）

得到的（第一种的）欧拉序是（将使用到的！！！，下文提及欧拉序时指的是这一种）：

2）每遇到一个节点就将它加入到序列中

得到的（第二种）欧拉序是：（了解即可）

//A B E B F K F B A C G C H C I C A

19-3-1-A 欧拉序的特点

• 这就不得不说它的作用：将 路径 查询转化为 区间 查询

选中上图中的 B节点，它的 子树（注：子树也包含顶节点）上有 B,E,F,K，欧拉序中两次出现B结点之间的序列为 (B) E E F K K F (B)，正是子树中的节点，且子树中 E K 是叶子节点，在欧拉序中两次出现是连续的！所以欧拉序很容易确定一个子树的组成节点有哪些。

我们需要两个变量分别记录下这两次出现的编号：

//用结构体集束化储存
int Ora_First;      //当前结点在欧拉序第一次出现的时候
int Ora_Second;     //当前结点在欧拉序第二次出现的时候

19-3-1-B 如何将 欧拉序 把 路径 转化到 区间（u,v）

假设：u=E，v=G，那么区间（E，G）的欧拉序为：

去掉两次出现的结点：{F K} ，再加上E 与 G的 最近共同祖先（接下来会介绍到） A 节点，就得到了E -> G的最短路径 E->B->A->C->G 。

19-3-1-B1 路径存在两种情况，区间也可能为反区间

如果查找的是 G到E的 路径，此时就是反区间 (G，E)，那就需要将端点位置交换，转换成正区间：

//伪代码
if( 第一个结点的Ora_First >= 第二个结点的Ora_First)
    swap(第一个结点，第二个结点);

这样使得 u 一定是 v 的祖先或者 u=v。

19-3-1-B2 欧拉序编号的使用

• 如果 u，v 在同一子树上（即 $LCA(u,v)=u$），路径在 欧拉序的区间$[u.Or{a}_{F}irst,v.Or{a}_{F}irst]$

  B结点的Ora_First=2，K结点的Ora_First=6，求 B->K 的路径就是在 区间[2,6] 中得到的

• 如果 u，v 在同一子树上（即 $LCA(u,v)!=u$ && $LCA(u,v)!=v$ ，或者说 $LCA(u,v)=root$），路径在 欧拉序的区间$[u.Or{a}_{S}econd,v.Or{a}_{S}econd]$

  K结点的Ora_Second=7，G结点的Ora_First=11，求 K->G 的路径就是在 区间[7,11] 中得到的

---

19-3-2 什么是最近公共祖先 LCA？

必须满足前提：是一棵***没有环***的树

• 举例：2号点 是 7号点和9号点 的最近公共祖先

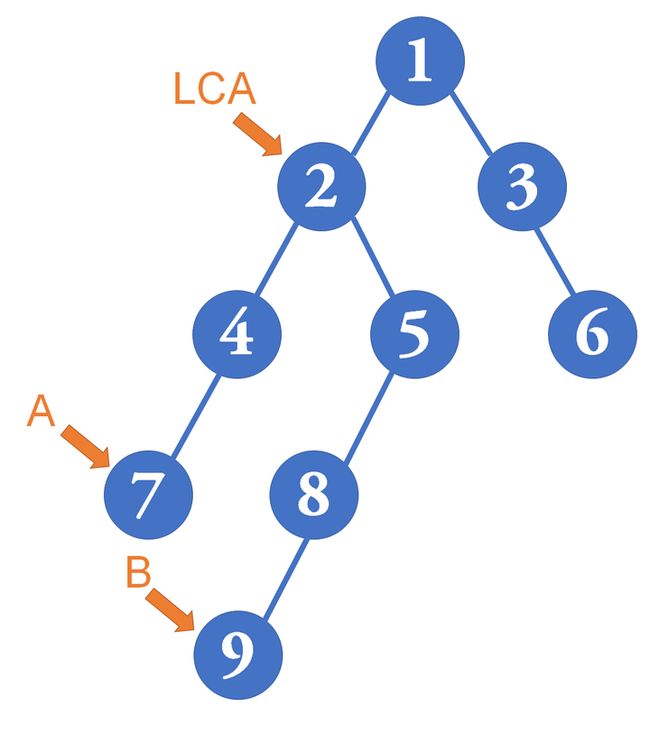
• LCA还可以是自己本身：2号点 是 2号点和9号点 的最近公共祖先

19-3-2-A 如何实现 最近公共祖先 LCA 的查询（4种算法）

重点是第四种算法！

19-3-2-A1 朴素算法 求 LCA

先让两者之间更深的那个先向上“爬"，直到两者的深度一致，再同时向上"爬"。

朴素算法预处理时需要 dfs 整棵树，时间复杂度为 $O(n)$，算法简单但浪费时间

//朴素的暴力法
//参考源：https://blog.csdn.net/ex_voda/article/details/126332116
struct node{
    vector<int> son;    //子节点
    int father;		    //父节点
    int depth;		    //深度
    node():depth(0){}   //无参构造函数初始化
} n_node[N];
int Find_Father(int id){
    if(id==n_node[id].father)       	   return id;//id是根节点       
    else	return Find_Father(n_node[id].father);  //回溯        
}
void DFS(int cur,int depth=0){				        //求出每个点的深度//初始化深度为0
    n_node[cur].depth=depth;
    for(size_t i=0;i<n[cur].son.size();i++)
		DFS(n_node[cur].son[i],depth+1);
}
int LCA(int x,int y){
    if(x==y)                                        //找到最近共同祖先    
        return x;
    if(n_node[x].depth==n[y].depth)                 //同深度时，一起回溯
        return LCA(n[x].father,n_node[y].father);
    else 							                //更深的结点先回溯
        return LCA(x,n_node[y].father);
}
int main(void){
    int n,m;	cin>>n>>m;
    for(int i=1;i<=n;i++){                          //初始化父节点
		n_node[i].father=i;
        n_node[i].son.clear();
    }
    while(m--){
        int father,son;     cin>>father>>son;
        n_node[son].father=father;
        n_node[father].son.push_back(son);
    }
    cin>>x>>y;							            //要查询x与y的LCA
    DFS(Find_Father(y));
    if(n_node[x].depth<=n_node[y].depth)
        cout<<LCA(x,y);
    else
        cout<<LCA(y,x);
    return 0;
}

19-3-2-A2 倍增算法 优化爬”为“跳”（朴素的plus版）

倍增算法 是一种牺牲空间换时间的算法。

倍增的意思是按 2的倍数 倍增：2、4、8、16，例如：n[x].depth - n[y].depth = 22，则可以让 结点x 向上依次回溯 16 、4 、2 个深度

//仅展示修改的部分
//对struct node结构体添加新成员
//参考源：https://blog.csdn.net/ex_voda/article/details/126332116
int f_d[16];			//（用于倍增跳跃）

//对功能（接口）函数的修改
int Delta_Depth(int x,int y){return n[y].depth - n[x].depth;}//深度差
void DFS(int cur,int depth=1)
void Jump_DFS(int cur,int depth=1){
	for(int i=1; (1<<i) <= n_node[x].depth; i++)
		n_node[x].f_d[i] = n_node[ n_node[x].f_d[i-1] ].f_d[i-1];
	for(size_t i=0; i<n_node[x].son.size(); i++)
		Jump_DFS(n_node[x].son[i], d+1);
}
int LCA(int x,int y){
	int d=Delta_Depth(x,y);				    //y比x深多少
    if(d!=0){
   		for(int i=(int)log2(d); i>=0; i--){
			if(n_node[ n_node[y].f_d[i] ].depth < n_node[x].depth)//跳过头了	
                continue; 	
			if(d==0)		break;  
			y = n_node[y].f_d[i];
			d=Delta_Depth(x,y);		        //更新高度差  
			i=(int)log2(d)+1;    	        //更新i 
		}
	}
	d = n_node[x].depth;	                        //节点到根节点的深度差 
	for(int i=(int)log2(d); i>=0; i--){ 
		if(x!=y && n_node[x].father==n_node[y].father)//碰面
            return n_node[x].parent;        
		if(x==y)	      continue;         //跳过头了       	
		x = n_node[x].f_d[i];
		y = n_node[y].f_d[i];
	}
	return 0;		//返回0则没找到
}

//主函数里的修改
memset(n_node[i].f_d, 0, sizeof(n_node[i].f_d))		//对f_d数组初始化
if(n_node[x].depth>n_node[y].depth)	swap(x,y);		//默认y的depth更大
DFS(Find(y));
Jump_DFS(Find(y));

19-3-2-A3 Tarjan算法 求 LCA

个人觉得这种算法纯sb

• 求 强连通分量 时， Tarjan算法 是 首选算法。

• Tarjan 是一种 离线算法：在输入完所有询问后，通过一次遍历给出所有答案。因此当你的询问条数很多时，Tarjan将更有优势！

• Tarjan算法 需要 强连通 、 两种DFS遍历方式 、 时间戳 的芝士

1 强连通（前提是有向图）与一些相关的芝士

借鉴源（图源自）：https://blog.csdn.net/m0_46761060/article/details/124712049

• 连通：无向图中，从任意点 i 可到达任一点 j

• 强连通：***有向图***中，从任意点 i 可到达任一点 j

• 弱连通：把有向图看作无向图时，从任意点 i 可到达任一点 j

如图，强连通无论那个点，都能按照方向到达任意一点，弱连通如果强行按方向，那么B到不了C，A到不了B和C，C到不了B。但如果把他看作是无向图，那么他们也能满足连通条件。

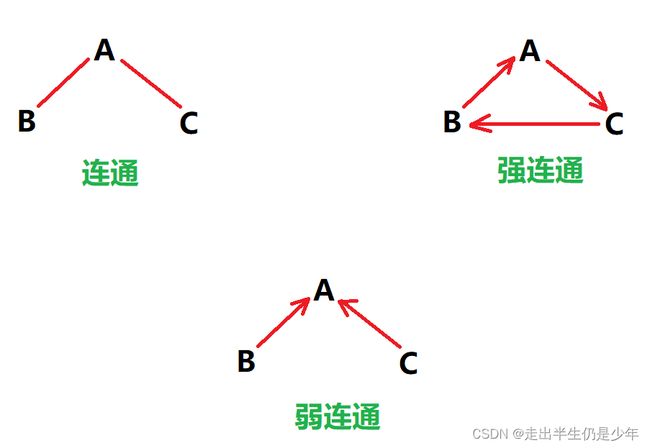
• 强连通分量（有向图中）

在 局部是强连通的 但 整体不是强连通的，也叫 有向图的极大强连通子图。

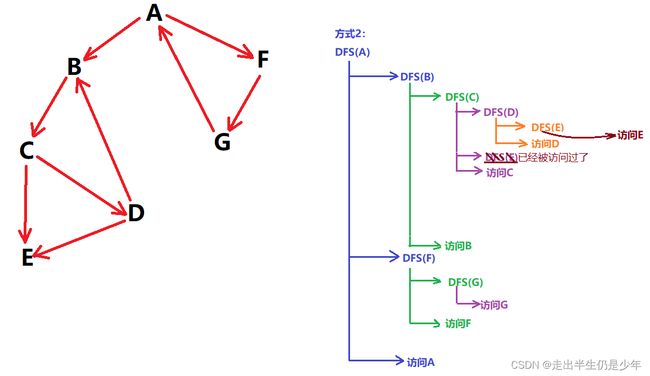
2 两种DFS遍历方式

• 先访问当前节点，再递归相邻节点

• 先递归相邻节点，再访问当前节点

• 法一：先访问当前节点，再递归相邻节点

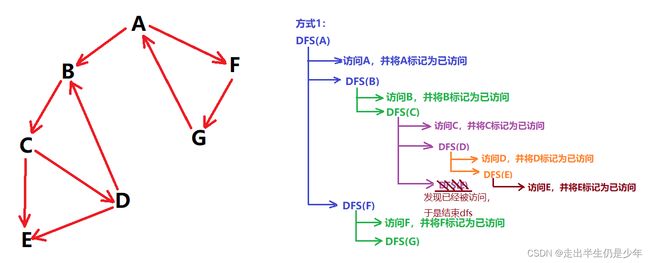
上面两个算法运用的就是法一，但 Tarjan算法 使用的法二。

• 法二：先递归相邻节点，再访问当前节点

输出的顺序变了，和 后序遍历 的顺序一致，这也是 Tarjan算法 的核心

3 结点 的 身份

对每个结点打上 [i,j] 的身份：i 是当前的 时间戳指针，j 是当前的 分量编号指针

• 时间戳 time

  在 带修改的莫队算法 我们也遇到过 时间戳 这个概念

在 有向图 的DFS中，记录每个结点 第一次 被访问的顺序编号，则这个 编号 就是这个结点的 时间戳。

• 注：每个点的时间戳不一定，取决于从哪个点开始遍历。时间戳可以帮我们判断这个点是否已经遍历过，有 visit[time]=true 的功能。

• 追溯值 low

  追溯值 实际上是 强连通分量的编号。分量编号的值相同的结点，他们同处于一个 强连通分量。

以上面法二的图为例：

按顺序A->B->C->D->E遍历到 E结点时，已经无法继续访问了，E结点与其他节点构不成强连通分量，赋予身份[5,5]。然后递归回溯，发现{B C D}同属一个强连通分量，他们的 j 值都为 2（追溯值 都记载为最初进入这个分量节点的时间戳，即节点B的时间戳）。

• 缩点的概念

这个图的强联通分量内，每个点都可以互相到达，这个分量可以浓缩成一个点。将一个由k个强连通分量组成的有向图缩成由k个点组成的有向图。

以上面法二的图为例，缩点概念图（注：缩点的编号是对应分量的追溯值low）：

• 注：缩点可以用 并查集 来实现！！！点击学习 并查集

4 Tarjan 实现 LCA查找 的 代码展示

//Input
7 6
1 2
1 3
2 4
2 5
3 6
3 7
2
5 6
4 5
//Output
1
2

#include
using namespace std;
const int N=1e5+5;
struct node{
    int father;
    //int time;             //时间戳
    vector<int> son;
    vector<int> m_node_id;  //记录单次询问中另一个节点的编号
} n_node[N];
vector<bool> visit(N,false);
vector<int> M(N);                                       //并查集MergeSet（合并同一个强连通分量的节点）,实现的功能是追溯值的计算
map<string,int> ans;                                    //（还原输入时的询问顺序）得到结果：下标是string类型，存放的数是整形的

queue<string> Q;									//存储询问
string Convert(int x, int y){                           //将两个独立的数转化成字符串：'x,y'，然后存入到询问容器中
	string str_x, str_y;
	stringstream _x, _y;
	_x<<x;	_y<<y;
	_x>>str_x;	_y>>str_y;
	return str_x+","+str_y;
}
void Init(int n){
    for(int i=1;i<=n;i++){
        M[i]=i;                                         //并查集的初始化
        n_node[i].father=i;
        n_node[i].son.clear();
    }
}

int Find_TopNode(int cur){
    if(cur==M[cur])     return cur;                     //查到顶节点。low值
    else                return Find_TopNode(M[cur]);    //向并查集的顶节点方向回溯 
}
void Tarjan(int cur){
    for(size_t i=0; i<n_node[cur].son.size(); i++){ 
        Tarjan(n_node[cur].son[i]);                      //递归查找到最深的子节点
        //将子节点绑在当前节点上，最终形成一串并查集，顶结点 就是 初入该强连通分量的节点
        M[ n_node[cur].son[i] ]=cur;
        //采用的就是法二的一直遍历直到遍历碰壁（但不标记当前节点已被遍历过），然后在递归回溯时将节点标记
        //同时回溯标记的方法也标记这个节点被合并了
        visit[ n_node[cur].son[i] ]=true;
    }
    for(size_t i=0; i<n_node[cur].m_node_id.size(); i++){
        int id=n_node[cur].m_node_id[i];
        if(visit[id]){                                  //如果标记合并过就返回顶节点
            int LCA=Find_TopNode(id);
            ans[ Convert(cur,id) ] = LCA;
            ans[ Convert(id,cur) ] = LCA;
        }//记录两次的原因：系统不能判定 'x,y' 和 'y,x'是一个意思（保证两种情况都能查到同一个答案）
    }
}
int main(void){
    int n,m;	        cin>>n>>m;
    Init(n);
    while(m--){
        int x,y;        cin>>x>>y;                      //分别输入父节点，子节点
        n_node[y].father=x;                             //x是y的父节点
        n_node[x].son.push_back(y);                     //y是x的子节点集其中的一个
    }
    int q;              cin>>q;
    int e,f;
    while(q--){                                         //记录询问
        cin>>e>>f;
        //无向图可以当做双有向
        n_node[e].m_node_id.push_back(f);
        n_node[f].m_node_id.push_back(e);
        Q.push(Convert(e,f));
    }
    int x_id=e;
    while(x_id!=n_node[x_id].father)					//找到遍历起始的根节点
        x_id=n_node[x_id].father;
    Tarjan(x_id);									
    while(!Q.empty()){
        cout<<ans[ Q.front() ]<<endl;
        Q.pop();
    }
    return 0;
}

• 又到了递归实验的环节

//测试的是1~3的慢二叉树
void Tarjan(int cur){
    for(size_t i=0; i<n_node[cur].son.size(); i++){ 
        Tarjan(n_node[cur].son[i]);
        M[ n_node[cur].son[i] ]=cur;
        visit[ n_node[cur].son[i] ]=true;
    }
    for(size_t i=0; i<n_node[cur].m_node_id.size(); i++){
        int id=n_node[cur].m_node_id[i];
        if(visit[id]){
            int LCA=Find_TopNode(id);
            ans[ Convert(cur,id) ] = LCA;	ans[ Convert(id,cur) ] = LCA;
        }
    }
}

第一次进入 Tarjan函数（cur=1，压入栈底），先进入第一个for循环，然后执行到第一句 Tarjan(...)，递归，第二次进入 Tarjan函数（此时cur=2，压入栈），进入循环，由于2号节点没有子节点退出循环，执行第二个循环，发现与2号节点同查询的结点未经访问，退出循环（2弹出栈）。

然后开始执行第一个循环内Tarjan(...)后的语句（弹出栈里唯一的元素1，cur=1），使得M[2]=1（此时并查集的顶节点为1，结点2的追溯值low=1），标记2（由于用的是DFS法二，标记是晚于访问到该节点的）。

后续操作可以自行脑补…

当然，如果觉得递归很抽象的话，可以手写个栈实现这个功能。

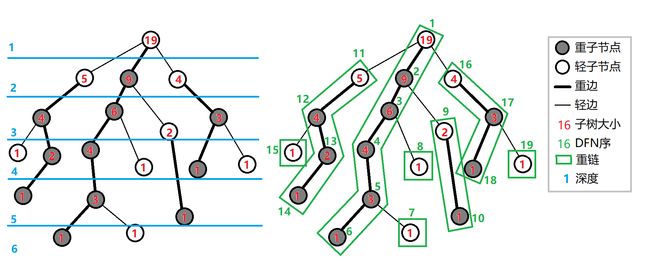
19-3-2-A4 树链剖分

参考blog：https://oi-wiki.org/graph/hld/

• 树链剖分 是 树上莫队 最关键的一步：它将 二维的树 降维为 一维的链

树链剖分（树剖/链剖）有多种形式，如 重链剖分，长链剖分 和用于 Link/cut Tree 的剖分（有时被称作「实链剖分」），大多数情况下（没有特别说明时），「树链剖分」都指「重链剖分」。

重链剖分可以将树上的任意一条路径划分成不超过 $O(logn)$ 条连续的链，每条链上的点深度互不相同（即是自底向上的一条链，链上所有点的 LCA 为链的一个端点)。

• 重链剖分还能保证划分出的每条链上的节点 DFS 序连续，因此可以方便地用一些维护序列的数据结构（如线段树）来维护树上路径的信息。如：

1. 修改 树上两点之间的路径上 所有点的值。
2. 查询 树上两点之间的路径上 节点权值的 和/极值/其它（在序列上可以用数据结构维护，便于合并的信息）。

1 重链（树上莫队需要的一种树链剖分的形式）

• 重子节点（重儿子）：一颗树的 子节点（即除根节点外的结点） 中 子树中 节点数目最多的节点。

  我的理解是：这个节点（有同一个父节点的子节点的比较）的 晚辈节点 是最多的。

  1）如果没有子节点（整个树就只有根节点1个节点的话），就无重子节点。

  2）（同一个父节点）有多个子节点满足这个重子节点的话，取其中一个当做重子节点

• 重边： 通向 重子节点 的边

  不是重边的一种情况：如果 轻子节点 是 重子节点 的子节点（比如上图中绿色标12与15）

• 轻边：通向 轻子节点 的边（即除 重边 外的边）

• 重链：连续的 重边 连在一起

  但是在处理时，会把落单的结点也当做一个重链，那么整棵树就被剖分成若干条重链！！！

• 轻链：通常作为桥梁连接下一个重链，长度一般为1（如1-16）

• 重链的头结点：$top$ ，例如：12-13-14链上top都为12

2 重链剖分 如何使用到 求LCA 中？

• 如何理解轻链的桥梁作用？

  解释参考源自：https://blog.csdn.net/qq_41418281/article/details/108220247，https://www.cnblogs.com/genius777/p/8719201.html（讲解的清晰点）

红链为重链，黄链为轻链，4-6这条轻链作为桥梁连接了 重子节点b 与 重链 1-2-4-5-a

• 求LCA

依照上图，求结点a与b的LCA：

• 情况一：二者同处于一条重链上（top相同），深度小者为LCA
• 情况二：不处于同一条重链（top不同），对其链顶深度大者操作，让其跳到链顶结点的父节点处（原因是防止链顶结点就是自己），然后回到根节点1进行判断，直到同链顶

int TreeLink_LCA(int x,int y){                              //树链剖分求最近公共祖先LCA
    while(D2[x].top!=D2[y].top){                            //不处于同一条重链（top不同）
        if(n_node[ D2[x].top ].depth > n_node[ D2[y].top ].depth)//链顶深度大者 跳到 链顶结点的父节点 处
            x=n_node[ D2[x].top ].father;
        else
            y=n_node[ D2[y].top ].father;
    }
    //此时同处同一条重链中 或 一开始就是同处一条重链中
    if(n_node[x].depth > n_node[y].depth)                   //深度小者为LCA
        return x;
    else    return y;
}

3 重链的构成

//定义
struct node{
    int val;                //输入的原始值
    int id;                 //将val离散化得到的编号
    int father;
    int depth;              //结点所处的深度
    node():depth(0){}
};
struct DFS1_node{
    int Hson;               //重子节点
    int ST_s;               //SonTree_Size子树大小（子树的结点数）
    int Ora_First;          //当前结点在欧拉序第一次出现的时候
    int Ora_Second;         //当前结点在欧拉序第二次出现的时候
    DFS1_node():Hson(0),ST_s(0){}
};
struct DFS2_node{
    int top;                //重链的链顶结点
    int rank;
    DFS2_node():top(0){}
};
vector<node> n_node;
vector<DFS1_node> D1;
vector<DFS2_node> D2;

• 第一个DFS 记录每个结点的 深度（depth）、子树大小（ST_s，初始化为1）、重子节点（Hson）

void Init_DFS(int cur=1,int f=0){                           //重链树剖 第一次 深搜：获得每个结点的 父结点、深度、重子节点、子树大小
    n_node[cur].father=f;
    n_node[cur].depth=n_node[f].depth+1;
    D1[cur].Ora_First=++Ora_id;                             //记录 cur结点 在 欧拉序 中 第一次 出现时的编号
    D1[cur].ST_s=1;                                         //初始化 结点的子树 的结点数为1（即他自己）
    
    vector<int>::iterator it;                               //迭代器（实际是指针）：用于遍历容器
    for(it=C[cur].begin(); it!=C[cur].end(); it++){         //遍历 当前结点 的 子结点【.begin():返回指向首元素的迭代器】
        int i_son=(*it);                                    //解引用 得到 迭代器（指针）指向元素的值
        if(f==i_son)                                        //（图存在有环的情况）绕了一圈又递归到环的起点了，就无需再递归了，退出当轮循环
            continue;                                       
        Init_DFS(i_son,cur);                                //返回到函数接口，继续向下递归
        
        D1[cur].ST_s+=D1[i_son].ST_s;                       //子结点 已被处理过了，用它来更新 父结点 的 子树大小
        if(D1[i_son].ST_s > D1[ D1[cur].Hson ].ST_s)        //cur结点 当前的这个子结点（i_son结点）的 子树的结点 是（目前）最多的（比上一个还要多）
            D1[cur].Hson=i_son;                             //将这个子结点 定义为 cur结点 的 重子结点
    }
    D1[cur].Ora_Second=++Ora_id;                            //记录 cur结点 在 欧拉序 中 第二次 出现时的编号
}

• 第二个 DFS 记录 所在重链的链顶（top，应初始化为结点本身）

void Link_DFS(int cur=1,int next=1){                        //重链树剖 第二次 深搜：获得 每条重链的链顶结点编号
    D2[cur].top=next;
    if(D1[cur].Hson)                                        //cur结点 的下方有 重链 
        Link_DFS(D1[cur].Hson, next);
    
    vector<int>::iterator it;
    for(it=C[cur].begin(); it!=C[cur].end(); it++){
        int i_son=(*it);
        if(i_son!=D1[cur].Hson && i_son!=n_node[cur].father)//当前的这个子结点 既不是 cur结点 的重子结点，也不是 它的父结点
            Link_DFS(i_son,i_son);
    }
}

19-3-3 离散化处理

这都基操了

//排序，去重，调函数
sort(S.data()+1, S.data()+1+n);                         //升序排序【.data()返回容器第一个元素的地址】
int uni=unique(S.data()+1, S.data()+1+n) - (S.data()+1);//去重操作
for(int i=1;i<=n;i++)                                   //离散化操作：编号从1开始
n_node[i].id=lower_bound(S.data()+1, S.data()+1+uni, n_node[i].val) - S.data();

19-3-4 Count on a tree II（HDU 6177）

题目描述

给定一个 $n$ 个节点的树，每个节点上有一个整数，$i$ 号点的整数为 $va{l}_i$。

有 $m$ 次询问，每次给出 $u^{\prime },v$，您需要将其解密得到 $u,v$，并查询 $u$ 到 $v$ 的路径上有多少个不同的整数。

解密方式：$u=u^{\prime }\mathrm{xor}lastans$。

$lastans$ 为上一次询问的答案，若无询问则为 $0$。

输入格式

第一行有两个整数 $n$ 和 $m$。

第二行有 $n$ 个整数。第 $i$ 个整数表示 $va{l}_i$。

在接下来的 $n-1$ 行中，每行包含两个整数 $u,v$，描述一条边。

在接下来的 $m$ 行中，每行包含两个整数 $u^{\prime },v$，描述一组询问。

输出格式

对于每个询问，一行一个整数表示答案。

样例输入 #1

8 2
105 2 9 3 8 5 7 7 
1 2
1 3
1 4
3 5
3 6
3 7
4 8
2 5
7 8

样例输出 #1

4
4

#include
using namespace std;
const int N=2e6;
struct node{
    int val;                //输入的原始值
    int id;                 //将val离散化得到的编号
    int father;
    int depth;              //结点所处的深度
    node():depth(0){}
};
struct DFS1_node{
    int Hson;               //重子节点
    int ST_s;               //SonTree_Size子树大小（子树的结点数）
    int Ora_First;          //当前结点在欧拉序第一次出现的时候
    int Ora_Second;         //当前结点在欧拉序第二次出现的时候
    DFS1_node():Hson(0),ST_s(0){}
};
struct DFS2_node{
    int top;                //重链的链顶结点
    int rank;
    DFS2_node():top(0){}
};
struct Query_node{
    int LCA;                //最近共同祖先
    int q_id;
    int l_id;
    int r_id;
    int l_block_id;
    int r_block_id;
};
vector<int> C[N];                                           //connect二维数组：原始输入的节点连接关系
vector<int> S;                                              //sort数组：用于后续离散化操作的排序数组
vector<node> n_node;
vector<DFS1_node> D1;
vector<DFS2_node> D2;
vector<Query_node> Q;                                       //存储询问的数组（同时也存储了输出时的顺序）
int Ora_id=0;

inline int Read(void){                                      //按顺序（去空格）读取有效整型数据
    int rt = 0, in = 1; char ch = getchar();
    while(ch < '0' || ch > '9') {if(ch == '-') in = -1; ch = getchar();}
    while(ch >= '0' && ch <= '9') {rt = rt * 10 + ch - '0'; ch = getchar();}
    return rt * in;
}

/*-----------------------重链剖分求LCA---------------------*/
void Init_DFS(int cur=1,int f=0){                           //重链树剖 第一次 深搜：获得每个结点的 父结点、深度、重子节点、子树大小
    n_node[cur].father=f;
    n_node[cur].depth=n_node[f].depth+1;
    D1[cur].Ora_First=++Ora_id;                             //记录 cur结点 在 欧拉序 中 第一次 出现时的编号
    D1[cur].ST_s=1;                                         //初始化 结点的子树 的结点数为1（即他自己）
    
    vector<int>::iterator it;                               //迭代器（实际是指针）：用于遍历容器
    for(it=C[cur].begin(); it!=C[cur].end(); it++){         //遍历 当前结点 的 子结点【.begin():返回指向首元素的迭代器】
        int i_son=(*it);                                    //解引用 得到 迭代器（指针）指向元素的值
        if(f==i_son)                                        //（图存在有环的情况）绕了一圈又递归到环的起点了，就无需再递归了，退出当轮循环
            continue;                                       
        Init_DFS(i_son,cur);                                //返回到函数接口，继续向下递归
        
        D1[cur].ST_s+=D1[i_son].ST_s;                       //子结点 已被处理过了，用它来更新 父结点 的 子树大小
        if(D1[i_son].ST_s > D1[ D1[cur].Hson ].ST_s)        //cur结点 当前的这个子结点（i_son结点）的 子树的结点 是（目前）最多的（比上一个还要多）
            D1[cur].Hson=i_son;                             //将这个子结点 定义为 cur结点 的 重子结点
    }
    D1[cur].Ora_Second=++Ora_id;                            //记录 cur结点 在 欧拉序 中 第二次 出现时的编号
}
void Link_DFS(int cur=1,int next=1){                        //重链树剖 第二次 深搜：获得 每条重链的链顶结点编号
    D2[cur].top=next;
    if(D1[cur].Hson)                                        //cur结点 的下方有 重链 
        Link_DFS(D1[cur].Hson, next);
    
    vector<int>::iterator it;
    for(it=C[cur].begin(); it!=C[cur].end(); it++){
        int i_son=(*it);
        if(i_son!=D1[cur].Hson && i_son!=n_node[cur].father)//当前的这个子结点 既不是 cur结点 的重子结点，也不是 它的父结点
            Link_DFS(i_son,i_son);
    }
}
int TreeLink_LCA(int x,int y){                              //树链剖分求最近公共祖先LCA
    while(D2[x].top!=D2[y].top){                            //不处于同一条重链（top不同）
        if(n_node[ D2[x].top ].depth > n_node[ D2[y].top ].depth)//链顶深度大者 跳到 链顶结点的父节点 处
            x=n_node[ D2[x].top ].father;
        else
            y=n_node[ D2[y].top ].father;
    }
    //此时同处同一条重链中 或 一开始就是同处一条重链中
    if(n_node[x].depth > n_node[y].depth)                   //深度小者为LCA
        return x;
    else    return y;
}

/*--------------------------莫队算法-----------------------------*/
int res=0;
vector<int> ans(N,0);                                       //查询区间的区间和
void Add( int ptr){      res+=n_node[ptr].val;}
void Sub( int ptr){      res-=n_node[ptr].val;}
void Move_Ptr(int m){                                       //指针的四种移动方向
    int pl=1,pr=0;                                          //左右指针，当前维护区间为[pl,pr]
    for(int i=0;i<m;i++){
        while(Q[i].l_id<pl)//向目标左端点左扩展
            Add(--pl);
        while(Q[i].r_id>pr)//向目标右端点右扩展
            Add(++pr);
        while(Q[i].l_id>pl)//向目标左端点右收紧
            Sub(pl++);
        while(Q[i].r_id<pr)//向目标右端点左收紧
            Sub(pr--);
        ans[ Q[i].q_id ]=res;                               //记录答案
    }
}   

int main(int argc, char* argv[]){
    int n=Read(), m=Read();

    for(int i=1;i<=n;i++)
        n_node[i].val=Read(), S[i]=n_node[i].val;

    sort(S.data()+1, S.data()+1+n);                         //升序排序【.data()返回容器第一个元素的地址】
    int uni=unique(S.data()+1, S.data()+1+n) - (S.data()+1);//去重操作
    for(int i=1;i<=n;i++)                                   //离散化操作：编号从1开始
        n_node[i].id=lower_bound(S.data()+1, S.data()+1+uni, n_node[i].val) - S.data();
    
    for(int i=1;i<=n;i++){                                  //输入树的信息
        int x=Read(), y=Read();
        //双向存储
        C[x].push_back(y);              
        C[y].push_back(x);
    }
    
    //获得树的所有信息
    Init_DFS();
    Link_DFS();

    int block_size=n*2 / sqrt(m*2/3);
    for(int i=1;i<=m;i++){
        int e=Read(), f=Read();
        if(D1[e].Ora_First >= D1[f].Ora_First)              //保证 e是f的祖先 或者 e=f
            swap(e,f);
        
        Q[i].q_id=i;
        Q[i].LCA=TreeLink_LCA(e,f);
        if(Q[i].LCA == e){                                  //f 在 e的子树里
            Q[i].l_id = D1[e].Ora_First;
            Q[i].r_id = D1[f].Ora_First;
            Q[i].l_block_id = Q[i].l_id/block_size;
            Q[i].r_block_id = Q[i].r_id/block_size;
            Q[i].LCA=0;
        }
        else{                                               //分别在根节点的左右子树
            Q[i].l_id = D1[e].Ora_Second;
            Q[i].r_id = D1[f].Ora_First;
            Q[i].l_block_id = Q[i].l_id/block_size;
            Q[i].r_block_id = Q[i].r_id/block_size;
        }                                                
    }    

    sort(Q.data()+1,Q.data()+1+m,
        [](Query_node Q1, Query_node Q2){               //对区间访问顺序进行了排序
            return Q1.l_block_id==Q2.l_block_id  ?  Q1.r_id<Q2.r_id : Q1.l_block_id<Q2.l_block_id;
        }
    );
    Move_Ptr(m);
    
    for(int i=1;i<=m;i++)
        cout<<ans[i];
    
    return 0;
}

19-3-5 补充说明

19-3-5-1 在编写代码时发现的错误

• 在编写算法的时候报了一堆 ‘变量名不明确’ 的错误。 变量名不明确 的原因一般有两种：

1）同时使用一个变量名表示两种不同的东西（尽管他们不是一个类型），比如：将节点结构体数组命名为n[N]，再将图中元素个数命名为 n

2）与库中内置的参数冲突了，比如：将并查集命名成 merge

19-3-5-2 arr.data()、arr.begin()、arr[0] 的区别

https://it.cha138.com/wen1/show-3379917.html