【算法系列】数据结构，包括链表、双向链表、栈、队列、并查集等

一、前言

数组模拟常见数据结构，包括链表、单链表、栈、队列、并查集等。

二、链表与邻接表

 单链表：可以用来写邻接表（存储图和树）
 双链表：用来优化某些问题
 head->o->o->空
 val[N]：用e[N]，表示某个点的值 ne[N]：某个点的next指针
 空结点下标用-1表示

2.1 单链表

2.1.1 常见操作

• 定义变量

const int N = 100010;

//head表示头结点的下标
//e[i] 表示i结点的值
//ne[i] 表示结点i的next指针是多少
//idx 存储当前已经用到了哪个点
int head,e[N],ne[N],idx;

• 初始化

//初始化
void init()
{
   head=-1;
   idx=0;
}

• 将x插到头结点

void add_to_head(int x)
{
    e[idx]=x;
    ne[idx]=head;
    head=idx;
    idx++;
}

• 将x插到下标是k的点的后面

void add(int k,int x)
{
    e[idx]=x;
    ne[idx]=ne[k];
    ne[k]=idx;
    idx++;
}

• 将下标是k的点的后面的点删除

void remove(int k)
{
   ne[k]=ne[ne[k]];
}

2.1.2 问题分析

注意：下标从0开始，因此第k个插入的点的下标是k-1。
代码：

#include 
#include 
#include 

using namespace std;

const int N = 100010;

//head表示头结点的下标
//e[i] 表示i结点的值
//ne[i] 表示结点i的next指针是多少
//idx 存储当前已经用到了哪个点
int head,e[N],ne[N],idx;

//初始化
void init()
{
    head=-1;
    idx=0;
}

//将x插到头结点
void add_to_head(int x)
{
    e[idx]=x;
    ne[idx]=head;
    head=idx;
    idx++;
}

//将x插到下标是k的点的后面
void add(int k,int x)
{
    e[idx]=x;
    ne[idx]=ne[k];
    ne[k]=idx;
    idx++;
}

//将下标是k的点的后面的点删除
void remove(int k)
{
    ne[k]=ne[ne[k]];
}

int main()
{
    int m;
    cin >> m;
    init();
    
    while(m--)
    {
        int k,x;
        char op;
        cin >> op;
        if(op=='H')
        {
            cin >> x;
            add_to_head(x);
        }
        else if(op=='D')
        {
            cin >> k;
            if(!k) head=ne[head];
            remove(k-1);
        }
        else
        {
            cin >> k >> x;
            add(k-1,x);
        }
    }
    for(int i=head;i!=-1;i=ne[i]) cout << e[i] << ' ';
    cout << endl;
}

2.2 双链表

2.2.1 常见操作

• 初始化

const int N = 100010;

int m;
int e[N],l[N],r[N],idx;

//初始化
void init()
{
    //0表示左端点，1表示右端点
    r[0]=1,l[1]=0;
    idx=2;
}

• 在下标为k的点的右边插入x 在下标为k的点的左边插入：add(l[k],x)

void add(int k,int x)
{
   e[idx]=x;
   r[idx]=r[k];
   l[idx]=k;
   l[r[k]]=idx;
   r[k]=idx;
   idx++;
}

• 删除第k个点

void remove(int k)
{
   r[l[k]]=r[k];
   l[r[k]]=l[k];
}

2.2.2 问题分析

代码：

#include 
#include 
#include 

using namespace std;

const int N = 100010;
int l[N],r[N],e[N],idx;

void init()
{
    r[0]=1;
    l[1]=0;
    idx=2;
}

void add(int k,int x)
{
    e[idx]=x;
    r[idx]=r[k];
    l[idx]=k;
    l[r[k]]=idx;
    r[k]=idx;
    idx++;
}

void remove(int k)
{
    r[l[k]]=r[k];
    l[r[k]]=l[k];
}

int main()
{
    int m;
    cin >> m;
    init();
    
    while(m--)
    {
        string op;
        int k,x;
        cin >> op;
        if(op=="L")
        {
            cin >> x;
            add(0,x);
        }
        else if(op=="R")
        {
            cin >> x;
            add(l[1],x);
        }
        else if(op=="D")
        {
            cin >> k;
            remove(k+1);
        }
        else if(op=="IL")
        {
            cin >> k >> x;
            add(l[k+1],x);
        }
        else
        {
            cin >> k >> x;
            add(k+1,x);
        }
    }
    for(int i=r[0];i!=1;i=r[i]) cout << e[i] << ' ';
    cout << endl;
}

三、栈与队列

栈：先进后出
队列：先进先出

3.1 堆栈

3.1.1 常见操作

• 堆栈中插入一个元素

stk[++tt]=x;

• 堆栈中删除一个元素

tt--;

• 判断栈是否为空

if(tt>0) not empty;
else empty;

• 取出栈顶元素

stk[tt];

3.1.2 模拟栈

代码：

#include 

using namespace std;

const int N = 100010;

int m;
int stk[N], tt;

int main()
{
    cin >> m;
    while (m -- )
    {
        string op;
        int x;

        cin >> op;
        if (op == "push")
        {
            cin >> x;
            stk[ ++ tt] = x;
        }
        else if (op == "pop") tt -- ;
        else if (op == "empty") cout << (tt ? "NO" : "YES") << endl;
        else cout << stk[tt] << endl;
    }

    return 0;
}

3.1.3 表达式求值

分析：

• 如何判断某颗子树被遍历完？ 当前运算符的优先级$<=$上一个运算的优先级。
• 括号的特殊处理：将栈内所有运算符从右往左操作一遍，直到遇到左括号为止。

关键：

• 双栈，一个操作数栈，一个运算符栈；
• 运算符优先级，栈顶运算符 和 即将入栈的运算符的优先级比较：①如果栈顶的运算符优先级低，新运算符直接入栈；②如果栈顶的运算符优先级高，先出栈计算，新运算符再入栈
  具体详解，参考链接

代码：

#include 
#include 
#include 
#include 
#include 

using namespace std;

stack<int> num;
stack<char> op;

void eval()
{
    auto b=num.top();num.pop();
    auto a=num.top();num.pop();
    auto c=op.top();op.pop();
    int x;
    if(c=='+') x=a+b;
    else if(c=='-') x=a-b;
    else if(c=='*') x=a*b;
    else x=a/b;
    num.push(x);//结果入栈
}

int main()
{
    unordered_map<char,int> pr{{'+',1},{'-',1},{'*',2},{'/',2}};//优先级表
    string str;//读入表达式
    cin >> str;
    for(int i=0;i<str.size();i++)
    {
        auto c=str[i];
        if(isdigit(c))//数字入栈
        {
            int x=0,j=i;
            while(j<str.size() && isdigit(str[j]))//计算数字
                x=x*10+str[j++]-'0';
            i=j-1;
            num.push(x);//数字入栈
        }
        else if(c=='(') op.push(c);//左括号入栈
        else if(c==')')//括号特殊，遇到左括号直接入栈，遇到右括号计算括号里面的
        {
            while(op.top()!='(') eval();//一直计算到左括号
            op.pop(); //左括号弹出
        }
        else
        {
            while(op.size() && pr[op.top()]>=pr[c]) eval();//待入栈运算符优先级低，则先计算
            op.push(c);//操作符入栈
        }
    }
    while(op.size()) eval();//将所有没有操作完的运算符，从右往左操作一遍
    cout << num.top();//栈顶元素即为答案
    return 0;
}

3.2 队列

3.2.1 常见操作

int q[N],hh,tt=-1;

• 在队尾插入元素，在队头弹出元素

//插入
q[++tt]=x;
//弹出
hh++;

• 判断队列是否为空

if(hh<=tt) not empty;
else empty;

• 取出队头元素

q[hh]
q[tt]

3.2.2 模拟队列

#
代码：

#include 
#include 
#include 

using namespace std;
const int N = 100010;
int q[N],hh,tt;
int n;

int main()
{
    cin >> n;
    hh=0,tt=-1;
    
    while (n -- )
    {
        string op;
        cin >> op;
        int x;
        if(op=="push")
        {
            cin >> x;
            q[++tt]=x;
        }
        else if(op=="pop")
        {
            hh++;
        }
        else if(op=="empty")
        {
            if(hh<=tt) cout << "NO" <<endl;
            else cout << "YES" <<endl;
        }
        else
        {
            cout << q[hh] << endl;
        }
    }
    return 0;
}

3.3 单调栈

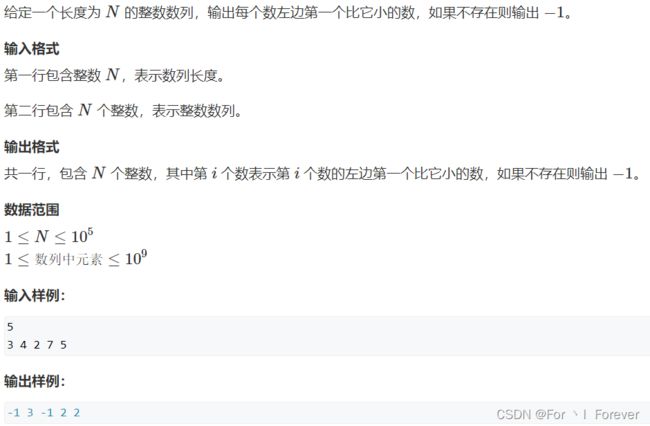
3.3.1 问题描述

• 情形： 给定一个序列，求出在序列中每一个左边离它最近且比它的数是什么？
• 例如： 3 4 2 7 5 ans：-1 3 -1 2 2
  

分析： 若存在$a_x>=a_y并且x<y$，那么$a_x$便可以被删除掉，即所有逆序的点都可以被删掉，依此来构建严格上升的单调栈。

如何寻找左边第一个比$a_i$小的数： 从栈顶开始寻找。若$stk[tt]>=a_i$，那么需要将$a_i$插入，因为$a_i$比栈顶元素小或相等，此时不断删除栈顶，直到找到一个$stk[tt]<a_i$。此时$stk[tt]$即为答案。

3.3.2 代码

#include 
#include 
#include 

using namespace std;

const int N = 100010;
int n;
int stk[N],tt;

int main()
{
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        int x;
        scanf("%d",&x);
        while(tt&&stk[tt]>=x) tt--;
        if(tt) printf("%d ",stk[tt]);
        else printf("-1 ");
        
        stk[++tt]=x;
    }
    return 0;
}

3.4 单调队列

3.4.1 问题描述

分析： 求解思路同上。

最小值和最大值分开来做，两个for循环完全类似，都做以下四步：

1. 解决队首已经出窗口的问题
2. 解决队尾与当前元素a[i]不满足单调性的问题
3. 将当前元素下标加入队尾
4. 如果满足条件则输出结果

注意： 上面四个步骤中一定要先3后4，因为有可能输出的正是新加入的那个元素；队列中存的是原数组的下标，取值时要再套一层，$a[q[]]$。

3.4.2 代码

#include 
#include 
#include 

using namespace std;

const int N = 1000010;
int a[N],q[N];
int n,k;

int main()
{
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    
    int hh=0,tt=-1;
    for(int i=0;i<n;i++)
    {
        //判断队头是否已划出滑动窗口
        if(hh<=tt && i-k+1>q[hh]) hh++;   // 若队首出窗口，hh加1
        while(hh<=tt && a[q[tt]]>=a[i]) tt--;// 若队尾不单调，tt减1
        q[++tt]=i;// 下标加到队尾
        if(i>=k-1) printf("%d ",a[q[hh]]); // 输出结果
    }
    puts("");
    
    hh=0,tt=-1;
    for(int i=0;i<n;i++)
    {
        //判断队头是否已划出滑动窗口
        if(hh<=tt && i-k+1>q[hh]) hh++;
        while(hh<=tt && a[q[tt]]<=a[i]) tt--;
        q[++tt]=i;
        if(i>=k-1) printf("%d ",a[q[hh]]);
    }
    puts("");
}

四、KMP

五、Trie树

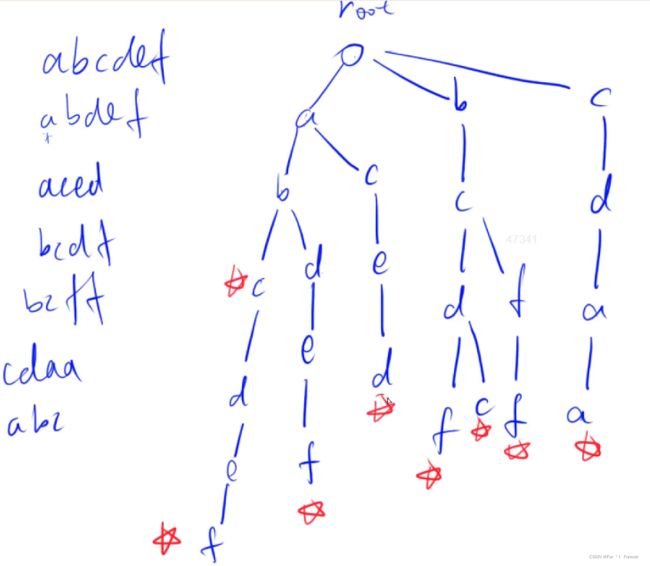
作用： 用来高效存储和查找字符串集合的数据结构

5.1 基础知识

5.1.1 存储方式

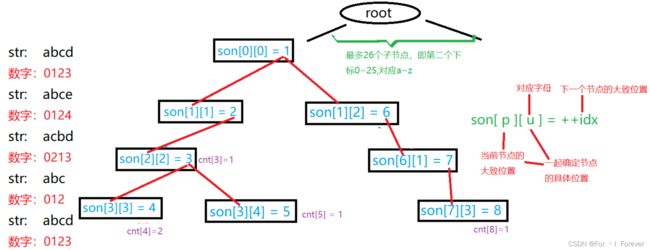
5.1.2 用数组来模拟Trie树的具体分析

5.2 常见操作

分析：
  Trie树中有个二维数组 son[N][26]，表示当前结点的儿子，如果没有的话，可以等于++idx。Trie树本质上是一颗多叉树，对于字母而言最多有26个子结点。所以这个数组包含了两条信息。比如：son[1][0]=2表示1结点的一个值为a的子结点为结点2;如果son[1][0] = 0，则意味着没有值为a子结点。这里的son[N][26]相当于链表中的ne[N]。

• 插入操作

void insert(char *str)
{
    int p = 0;  //类似指针，指向当前节点
    for(int i = 0; str[i]; i++)
    {
        int u = str[i] - 'a'; //将字母转化为数字
        if(!son[p][u]) son[p][u] = ++idx;
        //该节点不存在，创建节点,其值为下一个节点位置
        p = son[p][u];  //使“p指针”指向下一个节点位置
    }
    cnt[p]++;  //结束时的标记，也是记录以此节点结束的字符串个数
}

• 查询操作

int query(char *str)
{
    int p = 0;
    for(int i = 0; str[i]; i++)
    {
        int u = str[i] - 'a';
        if(!son[p][u]) return 0;  //该节点不存在，即该字符串不存在
        p = son[p][u]; 
    }
    return cnt[p];  //返回字符串出现的次数
}

5.3 Trie字符串统计

代码：

//Trie树快速存储字符集合和快速查询字符集合
#include 

using namespace std;

const int N = 100010;
//son[][]存储子节点的位置，分支最多26条；
//cnt[]存储以某节点结尾的字符串个数（同时也起标记作用）
//idx表示当前要插入的节点是第几个,每创建一个节点值+1
int son[N][26], cnt[N], idx;
char str[N];

void insert(char *str)
{
    int p = 0;  //类似指针，指向当前节点
    for(int i = 0; str[i]; i++)
    {
        int u = str[i] - 'a'; //将字母转化为数字
        if(!son[p][u]) son[p][u] = ++idx;   //该节点不存在，创建节点
        p = son[p][u];  //使“p指针”指向下一个节点
    }
    cnt[p]++;  //结束时的标记，也是记录以此节点结束的字符串个数
}

int query(char *str)
{
    int p = 0;
    for(int i = 0; str[i]; i++)
    {
        int u = str[i] - 'a';
        if(!son[p][u]) return 0;  //该节点不存在，即该字符串不存在
        p = son[p][u]; 
    }
    return cnt[p];  //返回字符串出现的次数
}

int main()
{
    int m;
    cin >> m;

    while(m--)
    {
        char op[2];
        scanf("%s%s", op, str);

        if(*op == 'I') insert(str);
        else printf("%d\n", query(str));
    }

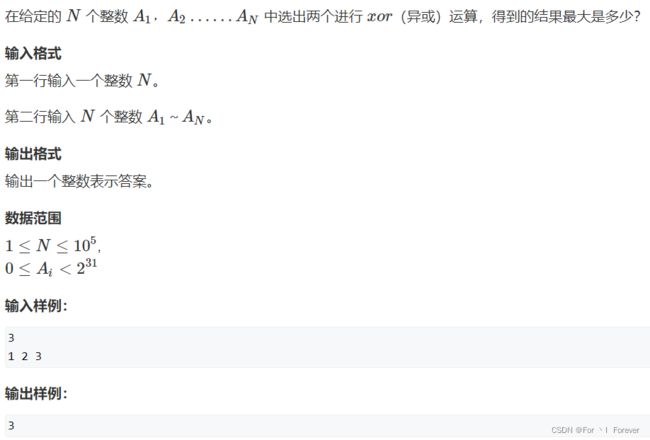
    return 0;
}

5.4 最大异或对

代码：

五、队列