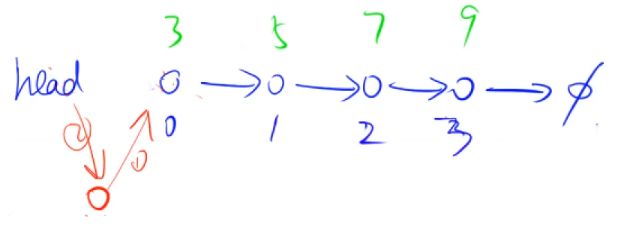数组模拟链表、栈、队列、单调队、栈

数组模拟链表、栈、队列、单调队、栈——打印资料

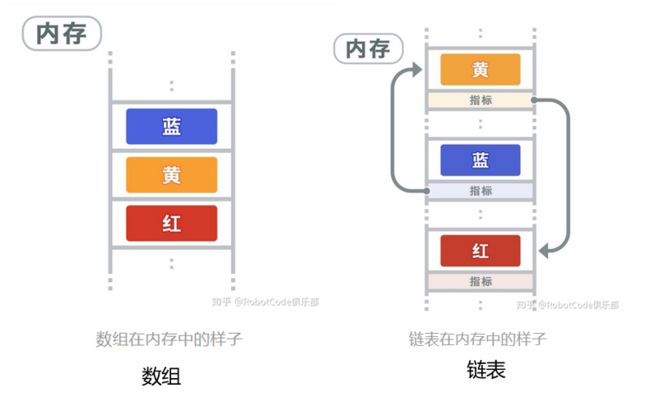
数组和链表的优劣对比

参考：https://zhuanlan.zhihu.com/p/73514867

数组的特点：

• 在内存中，数组是一块连续的区域。
• 插入和删除数据效率低（插入数据时，这个位置后面的数据都要后移）
• **查询效率很高。**因为数组是连续的，知道每一个数据的内存地址，可以直接找到给地址的数据(直接索引就能实现，不需要重头遍历)。
• 不利于扩展，一开始数组定义的空间不够时要重新定义数组。
• 会造成冗余。空间浪费。

链表的特点：

• 在内存中，不要求连续。
• 每一个数据都保存了下一个数据的内存地址(指针)，通过这个指针指向下一个数据。
• 增加和删除数据很容易。 （增加一个数，不需要动后面的数据，直接改变指针指向就行）
• 查找效率低，只能重头开始依次遍历寻找。
• 不指定大小，扩展方便。链表大小不用定义，数据随意增删。
• 空间使用灵活，不浪费。

数组和链表效率对比

数组模拟链表

原因：在信息学奥赛中，主要关注的是算法运行的速度、对于存储。只要求其不超过限制。因此，为了取得更快的运行速度，会采用用数组模拟链表。

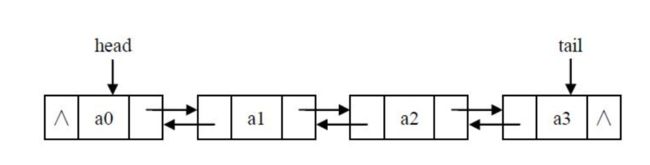
单链表

n 个结点链接成一个链表，这也就是平时书上所说的「链式存储结构」，因为这个链表中的每个结点中只包含一个指针域，所以又叫「单链表」。单链表正是通过每个结点的指针域将线性表的数据元素按其逻辑次序链接在一起。单链表的第一个结点的存储位置叫做「头指针」，最后一个结点的指针为「空」，一般用 “^” 表示。

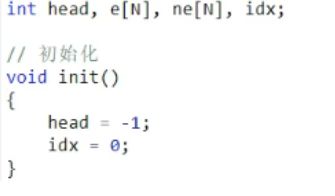
数组来模拟单链表

• e[i]数组代表编号i节点的值
• ne[i]数组代表编号i节点下一位置`的节点编号
• head表示头指针指向的节点编号
• idx是节点的编号，从0开始

初始化

插入到头

void add_head(int x){
    e[idx] = x; //记录节点的值
    ne[idx] = head; //步骤1
    head = idx;//步骤2
    idx++; //序号增长
}

插入到K节点的之后

void add(int x, int k){
    e[idx] = x;//记录节点的值
    ne[idx] = ne[k]; 
    ne[k] = idx;
    idx++;
}

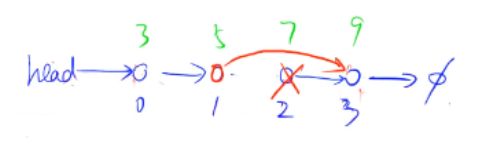
将下标是k的点后面的点，删掉

// 将下标是k的点后面的点删掉
void remove(int k)
{
    ne[k] = ne[ne[k]];//直接跳过k节点
}

习题

https://www.acwing.com/problem/content/description/828/

双链表

双向链表也叫 双链表 ，是链表的一种，它的每个数据结点中都有两个指针，分别指向直接后继和直接前驱。

注意：

• 头节点的前驱是 null
• 尾节点的后继是 null

初始化

• **e[i]**数组代表编号i节点的值
• L[i]数组代表编号i节点的左边的节点编号
• R[i]数组代表编号i节点的右边的 节点编号
• idx是节点的编号，从0开始

一开是初始化两个节点，分别是头、尾节点

void init()
{
    l[1]=0; // 1号节点 左边是 0号节点
    r[0]=1;// 0号节点右边是1号节点
    idx=2;//编号从2开始
}

插入K号节点右侧

void insert(int k,int x)//插入K号节点右侧
{
    //将新节点分别指向插入位置的右节点和左节点
    l[idx]=k;//操作1
    r[idx]=r[k];//操作2
    //将新节点右边一节点向左指向新节点,将新节点左边一节点向右指向新节点
    r[k]=idx;//操作3
    l[r[k]]=idx; //操作4
    idx++;//编号+1
    e[idx]=x;//记录节点的值 操作5
}

插入K号节点左侧

insert(k-1, x) ;

插入头节点右侧

insert(0,x);

插入尾节点左侧

void insertr(int x)
{
    r[idx]=1; //步骤1
    l[idx]=l[1];//步骤2
    l[1]=idx;//步骤3
    r[l[idx]]=idx;//步骤4
    e[idx++]=x;//步骤5
}

删除K号节点

void remove(int k)
{
    l[r[k]]=l[k];
    r[l[k]]=r[k];
}

习题

https://www.acwing.com/problem/content/description/829/

数组模拟栈

栈，栈就是一种只允许在表尾进行插入和删除操作的线性表。

• 栈顶和栈底，栈顶先出
• 加入一个元素，栈顶指针向上移动

初始化

用top表示栈顶所在的索引。初始时，top = -1。表示没有元素。

const int N = 100010;
int st[N]; //数组模拟栈
int top = -1;//栈顶起始位置，无元素

元素加入栈

push x ：栈顶所在索引往后移动一格，然后放入x。st[++top] = x。

st[++top] = a;//加入元素a

查看栈顶元素

query ： 返回栈顶元素。st[top]

cout << st[top];

删除栈顶

删除操作pop : top 往前移动一格。top–。

top--;

判空

empty ：top 大于等于 0 栈非空，小于 0 栈空。top == -1 ? “YES” : “NO”

cout << (top == -1 ? "YES" : "NO") << endl;

习题

https://www.acwing.com/problem/content/description/830/

https://www.acwing.com/activity/content/problem/content/3648/

队列

队列是一种先进先出的线性表（栈是先进后出）。它只允许在表的一端进行插入，或者删除元素。

• 从队尾进
• 从队头出
• 先进先出

初始化

const int N = 1e6;
int q[N];//数组模拟队
hh = tt = -1;//队头hh指向队头前一个元素、队尾tt指向最后一个元素

元素入队

q[++tt] = x;

查看队头元素

cout << q[hh+1];

删除队头元素

删除队头元素

hh++;

判空

头尾指针，相遇说明队列空了

cout << (tt == hh)? "yes":"no";

习题

https://www.acwing.com/problem/content/831/

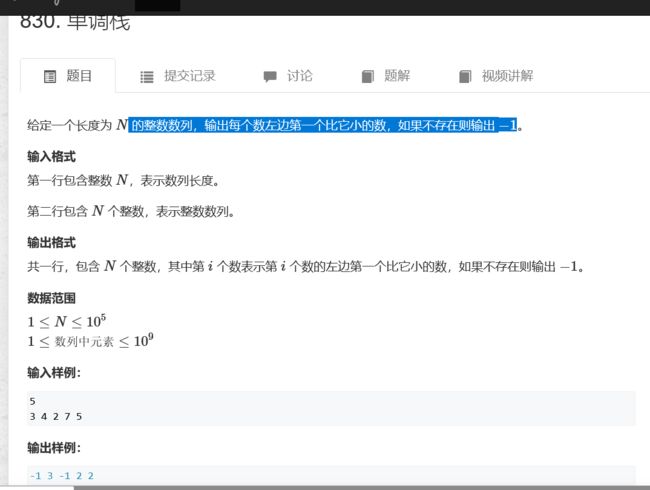
单调栈

栈中的元素，按题意的是单调的。

题目

输入
5
3 4 2 7 5
输出
-1 3 -1 2 2

想法

• 看到左边（或者之前），想到利用栈的结构，来存储之前的元素
• 由于是储存比它小的，那么可否让栈中元素，单调递增
  • 保持单调：栈顶大于等于当前元素，弹栈，再继续判断（while循环）
  • 如果栈内有元素，输出栈顶，反之输出 -1
• 最后当前元素入栈

代码

#include
using namespace std;
const int N = 10e5+10;
int st[N], tt = -1;
int main(){
    int n,x;
    cin >> n;
    while (n--){
        cin >> x;
        //不是单调的话，弹出	
        while (tt>=0 && st[tt] >= x) tt--;
        //弹出离它最近较小的数
        if(tt>=0) cout << st[tt]<<" ";
        //如果栈为空，则输出-1
        else cout << -1<< " ";
        //入栈
        st[++tt] = x;
    }
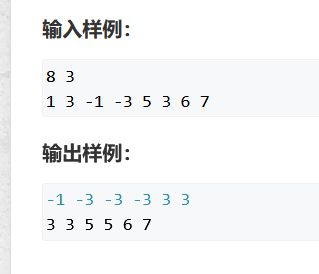
    return 0;
			
}

单调队列

题目

输入样例：
8 3
1 3 -1 -3 5 3 6 7
输出样例：
-1 -3 -3 -3 3 3
3 3 5 5 6 7

想法

想法一：暴力。O（n * k）

想法二：利用队列优化一下

• k元素的窗口中，输出最大值和最小值
• 那我们先以最大值举例
• 这种从后进，从前面出的模式和队列类似
• 队列出了窗口后，需要将出了窗口的元素剔除出去
• 队列保持单调减，让队头是整个 窗口的 最大值。
• 当窗口元素满足 k个，后再输出

那么就有下图：

代码

//https://www.acwing.com/solution/content/6564/
// Created by majoe on 2021/8/19.
//AcWing 154. 滑动窗口

#include 
using namespace std;
const int N = 10e6+10;
int a[N],q[N],tt=-1,hh; //q[i]表示单调队列中第i个元素的下标 ，a[i]是输入的数组
int main(){
    int n,k;//n个数，k为窗口长度
    cin >> n >> k;
    for (int i = 0; i < n; ++i) {
        scanf("%d",&a[i]);
    }
    //窗口内的最小值
    for (int i = 0; i < n; ++i) {
        //递增，求窗口内最小值
        if (i-k+1>q[hh]) ++hh; //窗口超出队头
        while(tt >=hh  && a[i]<=a[q[tt]]) tt--; //不满足单调性了
        q[++tt] = i;//下标加入队尾
        if(i+1>=k) printf("%d ",a[q[hh]]); //输出
    }
    cout << endl;
    hh =0, tt = -1; //重置
    for (int i = 0; i < n; ++i) {
        if(i-k+1>q[hh]) ++hh;
        //递减
        while(tt>=hh && a[i]>=a[q[tt]] ) tt--;
        q[++tt] = i;
        if(i+1>=k) printf("%d ",a[q[hh]]);
    }
    return 0;
}