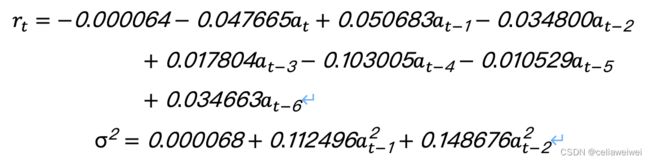金融时间序列分析:Python基于garch模型预测上证指数波动率、计算var和var穿透率、双尾检验
目录
一、收益率波动效应的分析
1.1 收益率序列平稳性检验
1.2 建立AR(p)模型
1.3 Ljung-Box混成检验残差序列的相关性,判断是否有ARCH效应
1.4 建立ARCH模型
二、GARCH模型与波动率预测
2.1 建立GARCH模型
2.2 波动率预测
三、正态分布的假设下通过波动率计算VaR
四、厚尾分布的假设下通过波动率计算VaR
五、同在一坐标系中画出股票的损失率图形及VaR图形
六、正态分布及厚尾分布下的VaR穿透率
本文的研究内容包括以下几个方面:
1.选择上证指数,利用GARCH模型对波动率进行预测;
2.在假设收益率满足正态分布的条件下,利用预测的波动率动态计算VaR;
3.选取适合的重尾分布(如t分布或Gumbel分布),假设收益率满足该分布,利用预测的波动率动态计算VaR;
4.在以上分析的基础上,进行相关图表的绘制;
5.统计正态分布和重尾分布条件下的VaR穿透率,并进行双尾检验。
本文围绕上述问题包含了一整套研究的流程,包括对数据的平稳性检验、残差检验、相关性分析、模型的定阶等。
文字通俗易懂,全面地指导了研究的进行,特别适合新手快速上手。
一、收益率波动效应的分析
通过进行收益率波动效应的分析,我们可以了解到收益率的波动是如何影响市场的,以及波动的原因和机制。
这有助于我们更好地理解金融市场的特点和规律,并为GARCH模型预测提供基础。
1.1 收益率序列平稳性检验
Python绘制收益率随日期变动趋势,如图所示:
根据图片可知,上证指数的收益率曲线呈现出明显的上下波动,波动的振幅较大,在相对短时间内频繁地在某一水平上下波动,形成一种震荡的走势,表明市场或者数据存在较大的不确定性。
通过进一步检验收益率序列的平稳性,决定是否需要进行差分。原假设H0:序列为非平稳的,备择假设H1:序列是平稳的。利用ADF检验可以判断任意时间序列的平稳性,一般情况下,非平稳时间序列存在单位根,可通过差分的方式消除单位根得到平稳序列。
计算得到p-value的值为0.0,小于显著性水平,故拒绝原假设,该收益率序列为平稳的非白噪声序列。
(关注gz号“finance褪黑素”回复222可获取本文全部数据和代码)
1.2 建立AR(p)模型
建立AR均值方程在时间序列分析中是非常常见和重要的步骤。AR均值方程可以用来描述序列的长期趋势和平均水平,可以揭示序列的长期趋势、对序列进行预测和模拟、准确地分离序列中的信号和噪声。通过分析模型系数,我们可以了能够揭示序列长期趋势、进行预测和模拟、分析信号和噪声、以及进行模型检验和优化等重要工具。这些都对我们更好地理解和解释时间序列数据非常有帮助。
根据该收益率序列的自相关函数进一步判定AR(p)模型的阶次,结果如图所示:
位于阴影内的第一个数为1,因此建立任意1阶及它之后的阶数都可以。作者尝试了几个阶数,发现7的效果最好(波动率的预测效果),因此建立AR(7)的模型。
1.3 Ljung-Box混成检验残差序列的相关性,判断是否有ARCH效应
数据序列具有ARCH效应是建立GARCH模型的前提条件之一。ARCH效应指的是序列中存在自相关的异方差性,即序列的波动程度与之前的波动程度相关。如果一个序列显示出ARCH效应,那么使用ARCH模型无法完全捕捉到其波动特征。
残差及残差平方的时间序列趋势如图所示:
对序列进行混成检验。原假设H0:序列没有相关性,备择假设H1:序列具有相关性。我们检验25个自相关系数:
通过观察上图,我们可以发现在所绘制的序列中,p-value的值均小于显著性水平0.05。由此推断,我们可以拒绝原假设,并且得出结论认为该序列具有相关性。进一步分析显示,残差平方的序列具有ARCH效应。这意味着序列中的波动性具有时间上的相关性和异方差性,即在不同的时间点上波动程度的大小存在明显差异。通过这一观察结果,我们可以深入研究波动模型,以更好地理解和解释序列的波动特性。
1.4 建立ARCH模型
通过对序列进行偏自相关函数(PACF)的分析,我们可以确定最适合的阶次。从下方图中可以观察到,PACF在3阶之后显著下降,因此我们可以将阶次定为3。
基于此结果,我们可以建立一个ARCH(3)模型,以更好地分析和描述序列的波动特征。ARCH(3)模型是一种常用的时间序列模型,它能够捕捉序列中的波动性和波动特征,从而提供更准确的预测和分析结果。通过使用这个模型,我们可以进一步研究和解释序列中的波动行为,并为后续的分析提供有力的基础。
模型结果如下:
根据回归结果得到以下方程:
对上述模型,我们可以看出,沪深300指数的日收益率期望大约在0.073%。并且回归模型的R-squared较小,拟合效果一般。根据拟合的方程进行预测并查看整体的预测拟合情况,从图中可以看出,虽然预测值和实际值的具体数值差距挺大,但是整体上均值和方差的变化相类似。
(关注gz号“finance褪黑素”回复222可获取本文全部数据和代码)
二、GARCH模型与波动率预测
2.1 建立GARCH模型
GARCH(m,s)模型的定阶较难,但是据学者们的实证研究结果,我们一般使用低阶模型GARCH(1,1),GARCH(2,1),GARCH(1,2)等就能够基本消除模型的波动性。下面我们构建均值方程为AR(7)模型,波动率模型为GARCH(1,1)的GARCH模型,回归结果如下:
最终我们得到波动率模型为:
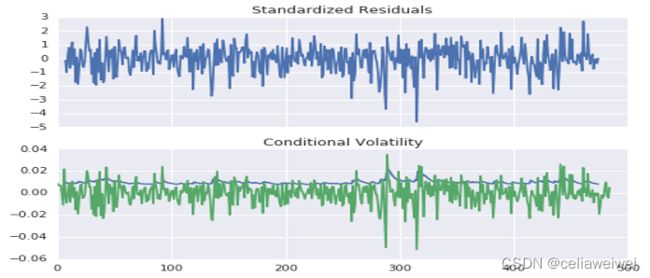
上面第一张图为标准化残差,近似平稳序列,说明模型在一定程度上是正确的;第二张图中绿色为原始收益率序列、蓝色为条件异方差序列,可以发现条件异方差很好得表现出了波动率。
上图为方差的拟合图,观察拟合图发现,模型在方差的还原上表现不错。
2.2 波动率预测
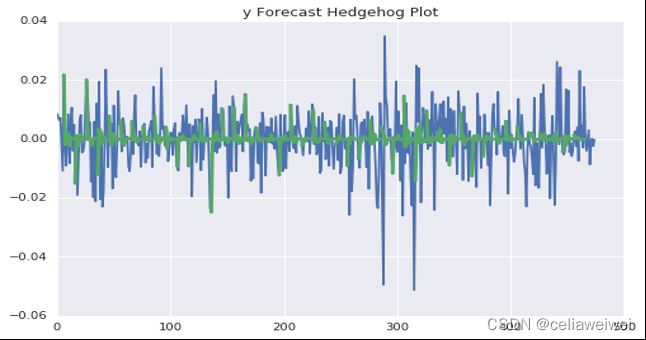
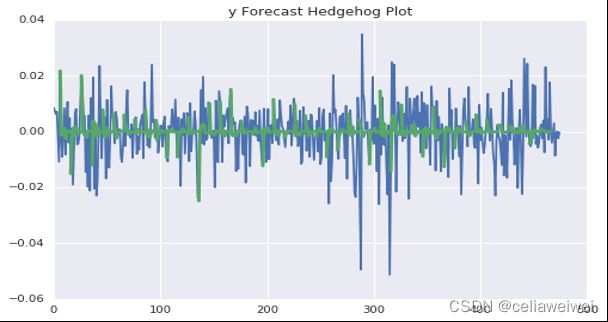
接着根据上面得到的波动率模型预测波动率,我们将原始数据、条件异方差拟合数据及预测数据一起画出来,进一步分析波动率预测情况。
图中红色部分为预测结果,可以看到最终的预测效果较好,基本符合原始数据的波动情况。
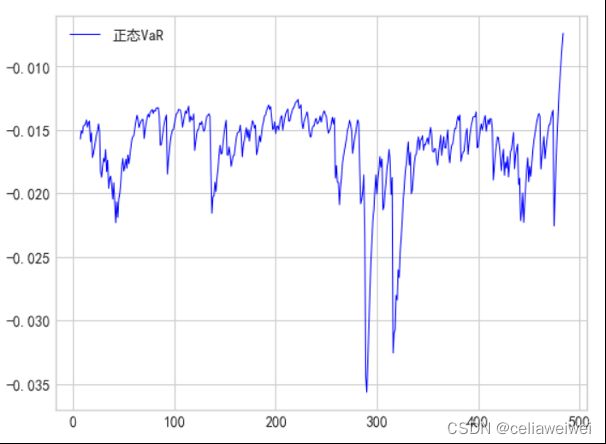
三、正态分布的假设下通过波动率计算VaR
利用序列的均值和标准差来描述其分布特征,通过选择置信水平来确定预测VaR的可靠性水平,常见的置信水平为95%或99%,再利用正态分布的累积分布函数逆函数(即Z-score)来计算对应于置信水平的VaR值。VaR代表在未来一定时间内,在给定置信水平下可能达到的最大损失。因此,通过将Z-score与波动率相乘,可以得到预测的波动率VaR。
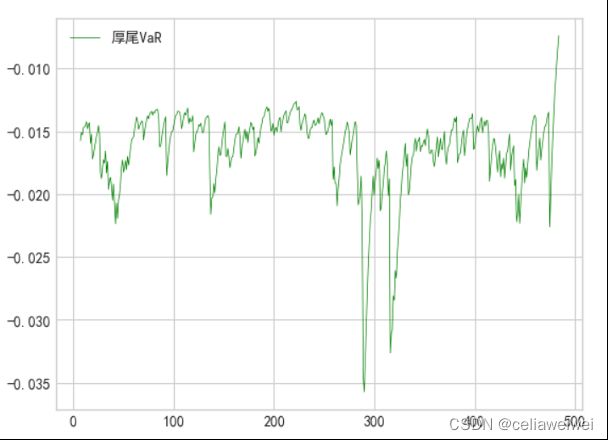
四、厚尾分布的假设下通过波动率计算VaR
假设股票收益率序列服从t分布的前提下,计算波动率VaR的方法如下:首先,假设股票收益率服从t分布,这种分布能够更好地考虑股票收益率的非正态特征,尤其是在尾部的厚尾现象。然后,通过选择置信水平来确定预测VaR的可靠性水平,常见的置信水平为95%或99%。接下来,利用自由度来描述t分布的形状,自由度通过收益率序列的长度减去1来计算。基于置信水平和自由度,使用t分布的累积分布函数逆函数(t-score)来计算对应于置信水平的VaR值。VaR代表在未来一定时间内,在给定置信水平下可能达到的最大损失。因此,通过将t-score与波动率相乘,可以得到预测的波动率VaR。
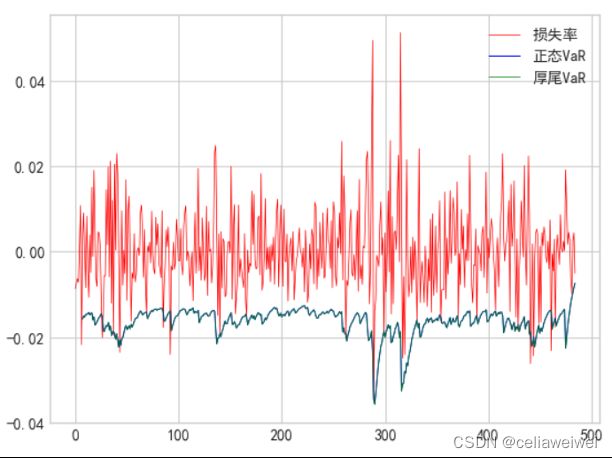
五、同在一坐标系中画出股票的损失率图形及VaR图形
六、正态分布及厚尾分布下的VaR穿透率
在金融风险管理领域,VaR(Value at Risk)是一种常用的风险度量指标,用于评估投资组合或资产在一定置信水平下的最大可能损失。在计算VaR时,常常需要假设股票收益率的概率分布模型。
在假设股票收益率服从正态分布的情况下,可以通过计算收益率序列的均值和标准差,确定在给定置信水平下的VaR值。VaR穿透率表示实际损失超过VaR值的概率。在正态分布假设下,较低的VaR穿透率表示较好的风险控制能力。然而,在实际情况中,股票收益率往往呈现出厚尾分布的特征,即存在较多的极端事件和离群值。为了更准确地估计风险,可以使用厚尾分布来近似股票收益率的分布特征。常用的方法是使用t分布来近似厚尾分布,通过选择合适的自由度参数来计算VaR值。由于考虑了较多的极端情况,厚尾分布下的VaR穿透率通常较高。
此外,为进一步检查收益率序列中是否存在显著的极端值,本文分别对其进行双尾检验。在正态分布假设下。可以使用标准正态分布表或正态分布的临界值进行双尾检验。而在厚尾分布假设下,需要使用t分布的临界值进行双尾检验。通过计算双尾检验通过率,可以评估超过临界值的极端事件的概率。较低的双尾检验通过率表示较小的极端事件风险。
沪深300指数的结果如下:
正态分布下的VaR穿透率: 0.05155
厚尾分布下的VaR穿透率: 0.20672
正态分布下的双尾检验通过率: 0.0
厚尾分布下的双尾检验通过率: 0.0
(关注gz号“finance褪黑素”回复222可获取本文全部数据和代码)