算法刷题记录 Hot--100
1. 同龄朋友
在社交媒体网站上有 n 个用户。给你一个整数数组 ages ,其中 ages[i] 是第 i 个用户的年龄。
如果下述任意一个条件为真,那么用户 x 将不会向用户 y(x != y)发送好友请求:
age[y] <= 0.5 * age[x] + 7
age[y] > age[x]
age[y] > 100 && age[x] < 100
否则,x 将会向 y 发送一条好友请求。
注意,如果 x 向 y 发送一条好友请求,y 不必也向 x 发送一条好友请求。另外,用户不会向自己发送好友请求。
返回在该社交媒体网站上产生的好友请求总数。
示例 1:
输入:ages = [16,16]
输出:2
解释:2 人互发好友请求。
示例 2:
输入:ages = [16,17,18]
输出:2
解释:产生的好友请求为 17 -> 16 ,18 -> 17 。
示例 3:
输入:ages = [20,30,100,110,120]
输出:3
解释:产生的好友请求为 110 -> 100 ,120 -> 110 ,120 -> 100 。
提示:
n == ages.length
1 <= n <= 2 * 104
1 <= ages[i] <= 120
- 解决方案:
class Solution {
public int numFriendRequests(int[] ages) {
//定义一个hashmap key存储 ages中的值,value存储ages中的值出现的次数
//使用getOrDefault(age,0) 来给value设置初始值,默认0
//getOrDefault(key.defaultValue)表示 当Map集合中有这个key时,就使用这个key值,如果没有就使用默认值defaultValue、
//当没出现相同的key时 让对应的value的值+1,来表示 出现的次数
HashMap<Integer, Integer> map = new HashMap<>();
for (int age : ages) {
map.put(age, map.getOrDefault(age, 0)+1);
}
int msg = 0;
/*
两次循环遍历map,使用keySet来获取所有的key值,表示获取ages数组中出现的年龄 并赋值给a 和 b
满足发送好友请求的条件为:
1、!b<=0.5*a+7
2、!b>100 && a<100
3、!b>a
满足该条件的 a 和 b 表示他们可以发送请求
通过map.get(a) 和 map.get(b) 获取 a 和 b 年龄 对应的在ages数组中有多少个
然后 map.get(a) * map.get(b) 其中有 a b 为同一个年龄的情况(key)减去a==b的情况就是总共发送的请求数
*/
for(int a : map.keySet()){
for( int b : map.keySet()){
if (check(a, b)){
msg += map.get(a)* (map.get(b) - (a==b?1:0));
}
}
}
return msg;
}
public boolean check(int a ,int b ){
return !(b<=0.5*a+7||b>100&&a<100 || b>a);
}
2. 两数之和
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
- 解决方案:
class Solution {
public int[] twoSum(int[] nums, int target) {
// 定义一个hashmap key 存nums的值,value存 下标
HashMap<Integer,Integer> map = new HashMap<>();
for(int i = 0 ; i < nums.length; i++){
map.put(nums[i],i);
}
// target - nums[] 中的差值 == map的key
//且 i != map.get(key)是表示 map中的索引和 数组的索引不相等
for(int i = 0 ; i < nums.length; i++){
int different = target - nums[i];
if(map.containsKey(different) && map.get(different) != i){
return new int[]{i,map.get(different)};
}
}
return null;
}
}
3. 两数相加
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:
输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
- 解决方案
public class ListNode {
int val;
ListNode next;
ListNode() {}
ListNode(int val) { this.val = val; }
ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}
/*
两数之和 --使用递归解决
1、两个数相加向下一个节点进一
2、当前结果的节点就是 l1.val + l2.val %10 的值
例子 9 + 9 = 18 18%10 = 8 8就是result几点的第一值
18/10 = 1 1就是需要向下一个节点进一的数,此时下一个节点的值(l1.next.val)+1 需要加上这个进一的值
3、然后开始递归计算下一个 result 结果的值 下一个l1节点的值就是 li.val + 进一的值
*/
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
int sum = l1.val + l2.val;
int jin1 = sum/10;
ListNode result = new ListNode(sum%10);
if (l1.next != null || l2.next != null || jin1 != 0){
l1 = l1.next != null ? l1.next : new ListNode(0);
l2 = l2.next != null ? l2.next : new ListNode(0);
l1.val += jin1;
result.next = addTwoNumbers(l1, l2);
}
return result;
}
4 . 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个子序列,不是子串。
示例 4:
输入: s = ""
输出: 0
- 解决方案
class Solution {
public int lengthOfLongestSubstring(String s) {
HashMap<Character,Integer> map = new HashMap<>();
int maxCount = 0;
for(int start = 0, end = 0 ; end < s.length(); end++){
char c = s.charAt(end);
// map包含字符 则表示该字符重复出现
// 这是就需要移动star位置+1 将窗口向前移动一位,表示出现过以start为起点的窗口出现过重复的字符
// 防止star 窗口后移 ( a b b a) 使用Math.max()后面的start 位置
if(map.containsKey(c)){
start = Math.max(map.get(c)+1,start);
}
//窗口向后移动一次就计算一次字符的长度,一直取最大值
maxCount = Math.max((end - start +1),maxCount);
//每次都将字符的存入map中 K:字符 V: 字符的下标
map.put(c,end);
}
return maxCount;
}
}
5.寻找两个正序数组的中位数 -4
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
- 解决方案
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
double median = 0;
//定义一个新数组,长度为nums1.length+nums2.length
//使用System.arraycopy()方法将数组nums1 和 nums2复制到新的数组
//System.arraycopy(源数组,源数组的起始位置,目标数组,目标数组的起始位置,要复制的源数组的个数)
int[] temp = new int[nums1.length+nums2.length];
System.arraycopy(nums1,0,temp,0,nums1.length);
System.arraycopy(nums2,0,temp,nums1.length,nums2.length);
//从小到大升序排列
Arrays.sort(temp);
// 中位数 :有序(升序)的数组中的中间的数
// 数组个数为奇数: 中位数就是中间的那个数
// 数组个数为偶数: 中位数就是中间那2个数据的算术平均值
if(temp.length%2 == 0 ){
median = (double)(temp[temp.length/2]+temp[(temp.length/2) - 1]) / 2;
}else{
median = (double)temp[temp.length/2];
}
return median;
}
}
6. 实现 Trie (前缀树) -208
Trie(发音类似 "try")或者说 前缀树 是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景,例如自动补完和拼写检查。
请你实现 Trie 类:
Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中,返回 true(即,在检索之前已经插入);否则,返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ,返回 true ;否则,返回 false 。
示例:
输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]
解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple"); // 返回 True
trie.search("app"); // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app"); // 返回 True
- 解决方案
class Trie {
// 定义私有的 TrieNode 类; 有两个私有成员
// boolean isEnd: 用来判断单词是否 插入/查找 完成 默认false
// TrieNode[] children: TrieNode数组,存储每一个节点的单词个数的TrieNode对象
private class TrieNode{
private boolean isEnd;
private TrieNode[] children;
// 无参构造函数初始化成员变量
// TrieNode[26] 数组长度26 26个字母
TrieNode(){
this.isEnd = false;
this.children = new TrieNode[26];
}
}
private TrieNode root;
// TrieClass 初始化赋值
public Trie() {
root = new TrieNode();
}
// 在前缀树 insert
public void insert(String word) {
// 当前节点为root
TrieNode currentNode = root;
for(int i = 0; i < word.length(); i++ ){
//获取每个单词的字母值 并减去 a 就是数组的下标
char ch = word.charAt(i);
int index = ch - 'a';
//如果当前节点的children[] 没有Trie对象 表示该节点没有该字母。
// 在当前节点的children[] 中插入Trie对象
if (currentNode.children[index] == null ) {
currentNode.children[index] = new TrieNode();
}
// 如果children[]中有值 则切换到该(值)trieNode节点
currentNode = currentNode.children[index];
}
// 循环结束 word 插入完成后 修改 isEnd 为true表示 到当前节点结束
currentNode.isEnd = true;
}
public boolean search(String word) {
TrieNode currentNode = root;
for(int i = 0 ; i < word.length(); i++){
char ch = word.charAt(i);
int index = ch - 'a';
if (currentNode.children[index] == null) {
return false;
}
currentNode = currentNode.children[index];
}
return currentNode.isEnd;
}
public boolean startsWith(String prefix) {
TrieNode currentNode = root;
for (int i = 0; i < prefix.length() ; i++) {
char ch = prefix.charAt(i);
int index = ch - 'a';
if (currentNode.children[index] == null) {
return false;
}
currentNode = currentNode.children[index];
}
return true;
}
}
}
7. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
示例 1:
输入:s = "babad"
输出:"bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入:s = "cbbd"
输出:"bb"
示例 3:
输入:s = "a"
输出:"a"
示例 4:
输入:s = "ac"
输出:"a"
提示:
1 <= s.length <= 1000
s 仅由数字和英文字母(大写和/或小写)组成
class Solution {
public String longestPalindrome(String s) {
int start = 0; //字符串截取的开始长度
int max = 0; //字符截取的最大长度
for (int i = 0; i < s.length(); i++) {
// 奇数回文 中间是字符有 i 控制 向两边扩散的距离由j 控制
// a b a 奇数的回文 长度为 2*j+1 中间有一个
// i-j i i+j 回文的开始长度为 i-1
for (int j = 0; i + j < s.length() && i - j >= 0; j++) {
if (s.charAt(i+j) == s.charAt(i-j)) {
int temLen = 2 * j + 1; // 长度是 2*j+1
if (temLen > max) {
max = temLen; // 大于需要截取的长度时赋值
start = i - j; // 跟新回文开始长度
}
}else{
break;
}
}
// 偶数回文 中间字符有两个 分别有 i 和 i+1 控制
// a b b a 偶数回文的长度: 2*j+2 中间有两个
//i-j i i+1 i+1+j 偶数回文在字符串中的起始长度:i-j
if(s.length() > 1) {
for (int j = 0; i+1 < s.length() && i - j >= 0 && i+1 +j <s.length(); j++ ) {
if (s.charAt(i- j) == s.charAt(i+1+ j) ) {
int tmpLen = 2 * j + 2;
if (tmpLen > max) {
max = tmpLen;
start = i - j;
}
} else{
break;
}
}
}
}
return s.substring(start,max + start);
}
}
8. 正则表达式匹配(不会做)
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
示例 1:
输入:s = "aa" p = "a"
输出:false
解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:s = "aa" p = "a*"
输出:true
解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:s = "ab" p = ".*"
输出:true
解释:".*" 表示可匹配零个或多个('*')任意字符('.')。
示例 4:
输入:s = "aab" p = "c*a*b"
输出:true
解释:因为 '*' 表示零个或多个,这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 5:
输入:s = "mississippi" p = "mis*is*p*."
输出:false
提示:
1 <= s.length <= 20
1 <= p.length <= 30
s 可能为空,且只包含从 a-z 的小写字母。
p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
保证每次出现字符 * 时,前面都匹配到有效的字符\
解决方案
9. 统计特殊四元组
给你一个 下标从 0 开始 的整数数组 nums ,返回满足下述条件的 不同 四元组 (a, b, c, d) 的 数目 :
nums[a] + nums[b] + nums[c] == nums[d] ,且
a < b < c < d
示例 1:
输入:nums = [1,2,3,6]
输出:1
解释:满足要求的唯一一个四元组是 (0, 1, 2, 3) 因为 1 + 2 + 3 == 6 。
示例 2:
输入:nums = [3,3,6,4,5]
输出:0
解释:[3,3,6,4,5] 中不存在满足要求的四元组。
示例 3:
输入:nums = [1,1,1,3,5]
输出:4
解释:满足要求的 4 个四元组如下:
- (0, 1, 2, 3): 1 + 1 + 1 == 3
- (0, 1, 3, 4): 1 + 1 + 3 == 5
- (0, 2, 3, 4): 1 + 1 + 3 == 5
- (1, 2, 3, 4): 1 + 1 + 3 == 5
提示:
4 <= nums.length <= 50
1 <= nums[i] <= 100
解决方案 直接暴力求解
/*
输入:nums = [1,1,1,3,5]
输出:4
解释:满足要求的 4 个四元组如下:
- (0, 1, 2, 3): 1 + 1 + 1 == 3
- (0, 1, 3, 4): 1 + 1 + 3 == 5
- (0, 2, 3, 4): 1 + 1 + 3 == 5
- (1, 2, 3, 4): 1 + 1 + 3 == 5
数组下标
*/
class Solution {
public int countQuadruplets(int[] nums) {
int max = 0;
for (int a = 0; a < nums.length; a++) {
for (int b = a + 1; b < nums.length; b++) {
for (int c = b+1; c < nums.length; c++) {
for (int d = c +1; d < nums.length; d++) {
if (nums[a] + nums[b] + nums[c] == nums[d]) {
max++;
}
}
}
}
}
return max;
}
}
10.剑指 Offer II 001. 整数除法
给定两个整数 a 和 b ,求它们的除法的商 a/b ,要求不得使用乘号 '*'、除号 '/' 以及求余符号 '%' 。
注意:
整数除法的结果应当截去(truncate)其小数部分,例如:truncate(8.345) = 8 以及 truncate(-2.7335) = -2
假设我们的环境只能存储 32 位有符号整数,其数值范围是 [−231, 231−1]。本题中,如果除法结果溢出,则返回 231 − 1
示例 1:
输入:a = 15, b = 2
输出:7
解释:15/2 = truncate(7.5) = 7
示例 2:
输入:a = 7, b = -3
输出:-2
解释:7/-3 = truncate(-2.33333..) = -2
示例 3:
输入:a = 0, b = 1
输出:0
示例 4:
输入:a = 1, b = 1
输出:1
提示:
-231 <= a, b <= 231 - 1
b != 0
解决方案
public int divide(int a, int b) {
// 32 位最大值:2^31 - 1 = 2147483647
// 32 位最小值:-2^31 = -2147483648
// -2147483648 / (-1) = 2147483648 > 2147483647 越界了
// 解决越界问题
// a 最小是:-2147483648
// 最大为: 2147483648-1 = 2147483647
// 使用负数计算会把最小值设为 -2147483648计算
if (a == Integer.MIN_VALUE && b == -1)
return Integer.MAX_VALUE;
// ab若为一正一负则返回-1
// ^(异或) 相同为true 不同为 false
// &(与) 必须两个都是true 才为true
// |(或) 有一个true 那就是true
// True ^ False = True
// False ^ True = True
// False ^ False = False
// True ^ True = False
int sign = (a > 0) ^ (b > 0) ? -1 : 1;
// 环境只支持存储 32 位整数
if (a > 0) a = -a;
if (b > 0) b = -b;
int res = 0;
// 使用减法代替除法
while (a <= b) {
a -= b;
res++;
}
return sign == 1 ? res : -res;
}
}
11. 将一维数组转变成二维数组
给你一个下标从 0 开始的一维整数数组 original 和两个整数 m 和 n 。你需要使用 original 中 所有 元素创建一个 m 行 n 列的二维数组。
original 中下标从 0 到 n - 1 (都 包含 )的元素构成二维数组的第一行,下标从 n 到 2 * n - 1 (都 包含 )的元素构成二维数组的第二行,依此类推。
请你根据上述过程返回一个 m x n 的二维数组。如果无法构成这样的二维数组,请你返回一个空的二维数组。
示例 1:
输入:original = [1,2,3,4], m = 2, n = 2
输出:[[1,2],[3,4]]
解释:
构造出的二维数组应该包含 2 行 2 列。
original 中第一个 n=2 的部分为 [1,2] ,构成二维数组的第一行。
original 中第二个 n=2 的部分为 [3,4] ,构成二维数组的第二行。
示例 2:
输入:original = [1,2,3], m = 1, n = 3
输出:[[1,2,3]]
解释:
构造出的二维数组应该包含 1 行 3 列。
将 original 中所有三个元素放入第一行中,构成要求的二维数组。
示例 3:
输入:original = [1,2], m = 1, n = 1
输出:[]
解释:
original 中有 2 个元素。
无法将 2 个元素放入到一个 1x1 的二维数组中,所以返回一个空的二维数组。
示例 4:
输入:original = [3], m = 1, n = 2
输出:[]
解释:
original 中只有 1 个元素。
无法将 1 个元素放满一个 1x2 的二维数组,所以返回一个空的二维数组。
提示:
1 <= original.length <= 5 * 104
1 <= original[i] <= 105
1 <= m, n <= 4 * 104
class Solution {
public int[][] construct2DArray(int[] original, int m, int n) {
int[][] arr = new int[m][n];
// 一位数组的个数不等于二维数组个数时 返回空
if (original.length != m*n) {
return new int[][]{};
}
int index = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (index < original.length){
arr[i][j] = original[index++];
}
}
}
return arr;
}
}
12. 剑指 Offer 03. 数组中重复的数字
在一个长度为 n 的数组 nums 里的所有数字都在 0~n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字重复了,也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。
示例 1:
输入:
[2, 3, 1, 0, 2, 5, 3]
输出:2 或 3
限制:
2 <= n <= 100000
class Solution {
public int findRepeatNumber(int[] nums) {
for (int i = 0; i < nums.length; i++ ) {
for (int j = i+1; j <nums.length;j++) {
if (nums[i] == nums[j]) {
return nums[i];
}
}
}
return 0;
}
}
13. 剑指 Offer 04. 二维数组中的查找
在一个 n * m 的二维数组中,每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个高效的函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
示例:
现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5,返回 true。
给定 target = 20,返回 false。
限制:
0 <= n <= 1000
0 <= m <= 1000
class Solution {
public boolean findNumberIn2DArray(int[][] matrix, int target) {
for (int i = 0; i < matrix.length;i++){ // matrix 行长度
for (int j = 0; j < matrix[i].length; j++) { // matrix列长度
//数组时顺序排列的大于每行的第一个小于最后一个说明 target 可能在本行中
if (target <= matrix[i][matrix[i].length-1] && target >= matrix[i][0]) {
if (matrix[i][j] == target) {
return true;
}
continue;
}
}
}
return false;
}
}
14. 剑指 Offer 05. 替换空格
请实现一个函数,把字符串 s 中的每个空格替换成"%20"。
示例 1:
输入:s = “We are happy.”
输出:“We%20are%20happy.”
class Solution {
public String replaceSpace(String s) {
return s.replace(" ","%20");
}
}
class Solution {
public String replaceSpace(String s) {
StringBuilder string = new StringBuilder();
for (int i = 0; i < s.length(); i++ ) {
char c = s.charAt(i);
if (c == ' ') {
string.append("%20");
}else {
string.append(c);
}
}
return string.toString();
// return s.replace(" ","%20");
}
}
15. 剑指 Offer 06. 从尾到头打印链表
输入一个链表的头节点,从尾到头反过来返回每个节点的值(用数组返回)。
示例 1:
输入:head = [1,3,2]
输出:[2,3,1]
限制:
0 <= 链表长度 <= 10000
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
class Solution {
public int[] reversePrint(ListNode head) {
// 定义一个节点并赋值为头节点
ListNode node = head;
// 定义一个数字下标索引
int index = 0;
// 节点不为空时说明有多少个节点 那么数字的空间就有多少 用index 记录
while(node != null){
node = node.next;
index++;
}
// 定义一个数组
int[] arr = new int[index];
//初始化节点
node = head;
// 数组从后向前赋值 并切换节点
for (int i = arr.length -1; i >= 0; i--) {
arr[i] = node.val;
node = node.next;
}
return arr;
}
}
16. 剑指 Offer 07. 重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例 2:
Input: preorder = [-1], inorder = [-1]
Output: [-1]
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
/**
二叉树前序遍历的顺序为:
先遍历根节点;
随后递归地遍历左子树;
最后递归地遍历右子树。
二叉树中序遍历的顺序为:
先递归地遍历左子树;
随后遍历根节点;
最后递归地遍历右子树。
*/
if (preorder.length == 0 || preorder == null) {
return null;
}
// 根据二叉树的先序遍历可知: 跟节点为先序数组的第一个元素
TreeNode root = new TreeNode(preorder[0]);
// 获取根节点在中序遍历数组的中位置
int root_index = 0;
for (int i = 0; i < inorder.length; i++) {
if (inorder[i] == preorder[0]) {
root_index = i;
}
}
// 根结点的左子树节点 = buildTree(左子树的先序数组,左子树的中序数组);
// 左子树的先序数组: preorder数组的第二个数开始(第一个数是根结点) 中序数组根结点前面的数组的个数(0 -> 中序节点的个数)
//
// 先序 3, 9, 20, 15, 7
//。 (0)root 1 2 3 4
// 中序 9, 3, 15, 20, 7
// 0 index1 2 3 4
// (原数组,开始复制的位置,到那结束(不包过该索引的值)) index+1 因为是源数组是从 1 开始赋值的
root.left = buildTree(Arrays.copyOfRange(preorder,1,root_index+1),
Arrays.copyOfRange(inorder,0,root_index));
root.right =buildTree(Arrays.copyOfRange(preorder,root_index+1,preorder.length),
Arrays.copyOfRange(inorder,root_index+1,inorder.length));
return root;
}
}
官方解决方案:
class Solution {
private Map<Integer, Integer> indexMap;
public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
if (preorder_left > preorder_right) {
return null;
}
// 前序遍历中的第一个节点就是根节点
int preorder_root = preorder_left;
// 在中序遍历中定位根节点
int inorder_root = indexMap.get(preorder[preorder_root]);
// 先把根节点建立出来
TreeNode root = new TreeNode(preorder[preorder_root]);
// 得到左子树中的节点数目
int size_left_subtree = inorder_root - inorder_left;
// 递归地构造左子树,并连接到根节点
// 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
// 递归地构造右子树,并连接到根节点
// 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
return root;
}
public TreeNode buildTree(int[] preorder, int[] inorder) {
int n = preorder.length;
// 构造哈希映射,帮助我们快速定位根节点
indexMap = new HashMap<Integer, Integer>();
for (int i = 0; i < n; i++) {
indexMap.put(inorder[i], i);
}
return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/zhong-jian-er-cha-shu-lcof/solution/mian-shi-ti-07-zhong-jian-er-cha-shu-by-leetcode-s/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
17. 剑指 Offer 09. 用两个栈实现队列
用两个栈实现一个队列。队列的声明如下,请实现它的两个函数 appendTail 和 deleteHead ,分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素,deleteHead 操作返回 -1 )
示例 1:
输入:
["CQueue","appendTail","deleteHead","deleteHead"]
[[],[3],[],[]]
输出:[null,null,3,-1]
示例 2:
输入:
["CQueue","deleteHead","appendTail","appendTail","deleteHead","deleteHead"]
[[],[],[5],[2],[],[]]
输出:[null,-1,null,null,5,2]
提示:
1 <= values <= 10000
最多会对 appendTail、deleteHead 进行 10000 次调用
时间 O(1) 插入删除
空间O(n)
// 维护两个栈 一个用来存元素 一个用来删除
// 以为栈 时先进后出。所以栈顶的元素就是队尾
// 删除的栈 在删除时将 存元素的站 的元素存入自身 此时栈顶的元素就是队列的头
// 栈1: 1 2 3 队尾
// 栈2:3 2 1 对头
class CQueue {
Stack<Integer> stack1; //用来插入队尾整数
Stack<Integer> stack2; //用来删除对头整数
int size; //表示列的大小
public CQueue() {
stack1 = new Stack();
stack2 = new Stack();
size = 0;
}
public void appendTail(int value) {
stack1.push(value);
size++;
}
public int deleteHead() {
// 队列没有元素 返回 -1
if (size == 0) return -1;
// 当栈2 没有元素时,把栈1的元素放入栈2
if (stack2.isEmpty()){
while (!stack1.isEmpty()) {
stack2.push(stack1.pop());
}
}
//队列删除元素 队列长度剪一
size--;
// 把栈2的顶部元素弹出。 表示删除队列头部元素
return stack2.pop();
}
}
/**
* Your CQueue object will be instantiated and called as such:
* CQueue obj = new CQueue();
* obj.appendTail(value);
* int param_2 = obj.deleteHead();
*/
18.消除游戏
列表 arr 由在范围 [1, n] 中的所有整数组成,并按严格递增排序。请你对 arr 应用下述算法:
从左到右,删除第一个数字,然后每隔一个数字删除一个,直到到达列表末尾。
重复上面的步骤,但这次是从右到左。也就是,删除最右侧的数字,然后剩下的数字每隔一个删除一个。
不断重复这两步,从左到右和从右到左交替进行,直到只剩下一个数字。
给你整数 n ,返回 arr 最后剩下的数字。
示例 1:
输入:n = 9
输出:6
解释:
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9]
arr = [2, 4, 6, 8]
arr = [2, 6]
arr = [6]
示例 2:
输入:n = 1
输出:1
提示:
1 <= n <= 109
思路:
核心思路:更新每次操作后的第一个元素值head初始值=1~
第一次操作(从左边到右依次删除):head = 2
第二次操作的时候(从右向左操作删除):
如果n(第二次操作时候的n,不是原始的n)是奇数,比如说2 4 6 (1 2 3 4 5 6操作而来)那么操作就会导致head值变换!head = head + 2= = 4
如果n(第二次操作时候的n,不是原始的n)是偶数,比如说2 4 6 8(1 2 3 4 5 6 7 8操作而来)那么操作就不会导致head值变换!head = 2
head 每次加上的值,就是公差值!即每操作一轮,公差值就会翻倍
可以总结说,head值只有在从左边操作 || 操作n为奇数 时才回发生改变!!!!最后head就是答案值
class Solution {
public int lastRemaining(int n) {
if (n == 1 ) {
return 1;
}
// 用来返回第一个数
int head = 1;
// 记录差值,每次循环(删除数)的时候 翻倍 *2
int step = 1;
// 记录从左到右 删除数字
boolean flag = true;
while (n > 1) {
// 只有当从左到右 或者从 右到左(n为奇数) 时才会改变 head 的值
if (flag || n%2 != 0) {
head += step;
}
// 差值翻倍
step*=2;
// 每次循环 就回删除一半的元素
n/=2;
// 删除方向改为 false 表示从右到左
flag = !flag;
}
return head;
}
}
19. 一周中的第几天
给你一个日期,请你设计一个算法来判断它是对应一周中的哪一天。
输入为三个整数:day、month 和 year,分别表示日、月、年。
您返回的结果必须是这几个值中的一个 {"Sunday", "Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday"}。
示例 1:
输入:day = 31, month = 8, year = 2019
输出:"Saturday"
示例 2:
输入:day = 18, month = 7, year = 1999
输出:"Sunday"
示例 3:
输入:day = 15, month = 8, year = 1993
输出:"Sunday"
提示:
给出的日期一定是在 1971 到 2100 年之间的有效日期。
思路:
题目规定输入的日期一定是在 19711971 到 21002100 年之间的有效日期,即在 19711971 年 11 月 11 日,到 21002100 年 1212 月 3131 日之间。通过查询日历可知,19701970 年 1212 月 3131 日是星期四,我们只需要算出输入的日期距离 19701970 年 1212 月 3131 日有几天,再加上 33 后对 77 求余,即可得到输入日期是一周中的第几天。
求输入的日期距离 19701970 年 1212 月 3131 日的天数,可以分为三部分分别计算后求和:
(1)输入年份之前的年份的天数贡献;
(2)输入年份中,输入月份之前的月份的天数贡献;
(3)输入月份中的天数贡献。
例如,如果输入是 21002100 年 1212 月 3131 日,即可分为三部分分别计算后求和:
(1)19711971 年 11 月 11 到 20992099 年 1212 月 3131 日之间所有的天数;
(2)21002100 年 11 月 11 日到 21002100 年 1111 月 3131 日之间所有的天数;
(3)21002100 年 1212 月 11 日到 21002100 年 1212 月 3131 日之间所有的天数。
其中(1)和(2)部分的计算需要考虑到闰年的影响。当年份是 400的倍数或者是 4 的倍数且不是 100 的倍数时,该年会在二月份多出一天
class Solution {
public String dayOfTheWeek(int day, int month, int year) {
String[] week = {"Monday", "Tuesday", "Wednesday", "Thursday", "Friday", "Saturday", "Sunday"};
int[] monthDays = {31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30};
/* 输入年份之前的年份的天数贡献 */
int days = 365 * (year - 1971) + (year - 1969) / 4;
/* 输入年份中,输入月份之前的月份的天数贡献 */
for (int i = 0; i < month - 1; ++i) {
days += monthDays[i];
}
if ((year % 400 == 0 || (year % 4 == 0 && year % 100 != 0)) && month >= 3) {
days += 1;
}
/* 输入月份中的天数贡献 */
days += day;
return week[(days + 3) % 7];
}
}
20.字符串替换 ? 且不能重复
class Solution {
public String modifyString(String s) {
char chars[] = s.toCharArray();
int len = chars.length;
for (int i = 0; i < n; i++) {
// 当前字符时 ?
if (chars[i] == '?') {
// 当前字符不是第一个字符
if (i > 0) {
// 让当前字符变为 上一个字符+1 的字母
chars[i] = chars[i-1] +1 > 'z' ? 'a' : (char) (chars[i-1]+1);
}else {
//表示当前字符为第一个字符 直接赋值a
chars[i] = 'a';
}
}
// 判断当前字母是否重复: chars【i-1】 == chars【ℹ】 == chars【i+1】
// 如果重复 让当前字母在加一
// 上一个 if 判断 已经让 当前字母不会和前一个相等了,现在只需要判断后一个
// i+1 < n 判断是否越界
if (i+1 < n && chars[i] == chars[i+1]) {
// 当前字母和后一个相同 在加一
chars[i] = chars[i+1] +1 > 'z' ? 'a' : (char) (chars[i-1]+1);
}
}
return String.valueOf(chars);
}
}
21. 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。
class Solution {
// 使用二分查找发
public int search(int[] nums, int target) {
//数组时有序的 如果给定的值小与第一个元素或大于最后一个元素返回-1
if (target < nums[0] || target > nums[nums.length - 1]) {
return -1;
}
// 左右指针
int left = 0;
int right = nums.length - 1;
while (left <= right) {
// 中间指针 = left + (right - left)/2;
int mid = left + (right - left)/2;
if (nums[mid] == target) {
return mid;
}else if (nums[mid] < target){ // 中间值小于target 说明在中间值的右边
left = mid + 1;
}else if (nums[mid] > target) { // 中间值大于target 说明在中间值的左边
right = mid - 1;
}
}
return - 1;
}
}
22.括号的最大嵌套深度
题意为:字符串中的括号深度。
如: S = “( )” 这个字符串的括号深度为 1 :只有一个括号
S = “( () )+( )” : 这个字符串的括号深度为 2
如果字符串满足以下条件之一,则可以称之为 有效括号字符串(valid parentheses string,可以简写为 VPS):
字符串是一个空字符串 "",或者是一个不为 "(" 或 ")" 的单字符。
字符串可以写为 AB(A 与 B 字符串连接),其中 A 和 B 都是 有效括号字符串 。
字符串可以写为 (A),其中 A 是一个 有效括号字符串 。
类似地,可以定义任何有效括号字符串 S 的 嵌套深度 depth(S):
depth("") = 0
depth(C) = 0,其中 C 是单个字符的字符串,且该字符不是 "(" 或者 ")"
depth(A + B) = max(depth(A), depth(B)),其中 A 和 B 都是 有效括号字符串
depth("(" + A + ")") = 1 + depth(A),其中 A 是一个 有效括号字符串
例如:""、"()()"、"()(()())" 都是 有效括号字符串(嵌套深度分别为 0、1、2),而 ")(" 、"(()" 都不是 有效括号字符串 。
给你一个 有效括号字符串 s,返回该字符串的 s 嵌套深度 。
示例 1:
输入:s = "(1+(2*3)+((8)/4))+1"
输出:3
解释:数字 8 在嵌套的 3 层括号中。
示例 2:
输入:s = "(1)+((2))+(((3)))"
输出:3
示例 3:
输入:s = "1+(2*3)/(2-1)"
输出:1
示例 4:
输入:s = "1"
输出:0
class Solution {
public int maxDepth(String s) {
int deep = 0 , ans = 0;
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c == '(') {
deep++;
ans = Math.max(ans,deep);
}
if (c == ')') {
deep--;
}
}
return ans;
}
}
23.移除元素
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
说明:
为什么返回数值是整数,但输出的答案是数组呢?
请注意,输入数组是以「引用」方式传递的,这意味着在函数里修改输入数组对于调用者是可见的。
你可以想象内部操作如下:
// nums 是以“引用”方式传递的。也就是说,不对实参作任何拷贝
int len = removeElement(nums, val);
// 在函数里修改输入数组对于调用者是可见的。
// 根据你的函数返回的长度, 它会打印出数组中 该长度范围内 的所有元素。
for (int i = 0; i < len; i++) {
print(nums[i]);
}
示例 1:
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如,函数返回的新长度为 2 ,而 nums = [2,2,3,3] 或 nums = [2,2,0,0],也会被视作正确答案。
示例 2:
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。
class Solution {
// 使用快慢指针完成替换数组元素
public int removeElement(int[] nums, int val) {
int slow ; //慢指针用来表示数组返回的下标
int fast = 0;
for (slow = 0; fast < nums.length; fast ++) {
// 当 fast 的值不等于 val 时,fast值赋值个 slow的值 ,slow 和 fast 同时向后移动
// 当 fast 的值 等于 val 时, 只有fast 的值往后移动,slow指向需要覆盖的值/
// 最后 slow的值就值去除 val 值 后的数组长度
if (nums[fast] != val) {
nums[slow] = nums[fast];
slow++;
}
}
return slow;
}
}
24. 判定字符是否唯一
实现一个算法,确定一个字符串 s 的所有字符是否全都不同。
示例 1:
输入: s = “leetcode”
输出: false
示例 2:
输入: s = “abc”
输出: true
限制:
0 <= len(s) <= 100
如果你不使用额外的数据结构,会很加分。
使用set去重功能完成
class Solution {
public boolean isUnique(String astr) {
// astr 为空直接返回false
if (astr == null) return false;
// 定义一个hashset 用来存储 astr 字符串中的每一个值
// set自带了去重的功能,
//存储完 astr 的值后set的size如果和astr的长度相等则没有重复的
HashSet set = new HashSet<String>();
for (int i = 0; i < astr.length(); i++) {
set.add(astr.charAt(i));
}
if(set.size() == astr.length()){
return true;
}
return false;
}
}
使用数组来代替set
public boolean isUnique(String s) {
int n = s.length();
if (n > 26) return false;
int[] cnt = new int[26];
for (int i = 0; i < n; i++) {
int ind = s.charAt(i) - 'a';
if (cnt[ind] != 0) return false; // // 此时表示该字母在前面已经出现过了 就直接return false
cnt[ind]++;
}
return true;
}
## 25. 长度最小的子数组给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:
输入:target = 4, nums = [1,4,4]
输出:1
示例 3:
输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0
提示:
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105
暴力求解 时间 O(n^2) 空间 O(1)
class Solution {
public int minSubArrayLen(int target, int[] nums) {
if (nums.length == 0 ){
return 0;
}
int ans = Integer.MAX_VALUE; // 因为每次要取最小值
for (int i = 0; i< nums.length; i++) {
int sum = 0;
for (int j = i; j < nums.length; j++) {
sum+=nums[j]; // 每次累加
if (sum >= target){
int tem = 0;
tem = j-i+1; // 获取当前子串的长度
ans = Math.min(tem,ans);
break;
}
}
}
return ans == Integer.MAX_VALUE ? 0 : ans;
}
}
class Solution {
public int minSubArrayLen(int target, int[] nums) {
// 滑动窗口
int left = 0; // 左指针 指向第一个元素 当右指针的元素 > target时,右指针的元素和减去当前左指针指向的元素 并左指针后移一位
int right = 0; // 有指针 计算累加值
int ans = Integer.MAX_VALUE;
int sum = 0;
for (;right < nums.length; right++){
sum += nums[right];
while(sum >= target){
int tem =0;
tem = right - left + 1; // 当前子串的长度
ans = Math.min(ans,tem); // 去最小值
sum = sum-nums[left++]; // 右指针的元素和减去当前左指针指向的元素 并左指针后移一位
}
}
return ans == Integer.MAX_VALUE ? 0 : ans;
}
25.螺旋矩阵 II 原题:
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,
且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
class Solution {
public int[][] generateMatrix(int n) {
int[][] matrix = new int[n][n];
// 定义四个边界 上下左右
// 顺时针顺序排列就是按照 从左到右,从上到下,从右到左,在从下到上的顺序给数组赋值
// 每一次循环完成 就收缩边界
// 当上下边界相等时,左右边界也会相等
// 如果矩阵的行列数是奇数的话 中间会空一个 需要单独赋值
if (n % 2 != 0 ) matrix[n/2][n/2] = n*n;
int top = 0 ; // 上边界向下收缩 (矩阵的行)
int bottom = matrix.length - 1; //下边界从下向上收缩,初始长度时矩阵的最大行数。(矩阵的行)
int left = 0; // 左边界是矩阵左边的列;(矩阵的列)
int right = matrix.length - 1; // 右边界是矩阵最右边的列(每行的最大值),向左收缩 (矩阵的列)
int num = 1;
// 四个边界向中间收缩
while (left < right && top < bottom) {
// 从左到右
for (int i = left; i < right;i++) {
// 从左到右赋值 都是在上边界上赋值
matrix[top][i] = num++;
}
//从上到下
for (int i = top; i < bottom; i++) {
// 是在右边界上从上到下赋值
matrix[i][right] = num++;
}
// 从右到左
for (int i = right; i > left; i--) {
// 在下边界 从右到左赋值
matrix[bottom][i] = num++;
}
//从上到下
for (int i = bottom; i > top; i--) {
// 在左边界上 从下到上赋值
matrix[i][left] = num++;
}
// 收缩边界
top++;
left++;
bottom--;
right--;
}
return matrix;
}
}
26. 按键持续时间最长的键 原题
给你一个长度为 n 的字符串 keysPressed ,其中 keysPressed[i] 表示测试序列中第 i 个被按下的键。releaseTimes 是一个升序排列的列表,其中 releaseTimes[i] 表示松开第 i 个键的时间。字符串和数组的 下标都从 0 开始 。第 0 个键在时间为 0 时被按下,接下来每个键都 恰好 在前一个键松开时被按下。
测试人员想要找出按键 持续时间最长 的键。第 i 次按键的持续时间为 releaseTimes[i] - releaseTimes[i - 1] ,第 0 次按键的持续时间为 releaseTimes[0] 。
注意,测试期间,同一个键可以在不同时刻被多次按下,而每次的持续时间都可能不同。
请返回按键 持续时间最长 的键,如果有多个这样的键,则返回 按字母顺序排列最大 的那个键。
输入:releaseTimes = [9,29,49,50], keysPressed = "cbcd"
输出:"c"
解释:按键顺序和持续时间如下:
按下 'c' ,持续时间 9(时间 0 按下,时间 9 松开)
按下 'b' ,持续时间 29 - 9 = 20(松开上一个键的时间 9 按下,时间 29 松开)
按下 'c' ,持续时间 49 - 29 = 20(松开上一个键的时间 29 按下,时间 49 松开)
按下 'd' ,持续时间 50 - 49 = 1(松开上一个键的时间 49 按下,时间 50 松开)
按键持续时间最长的键是 'b' 和 'c'(第二次按下时),持续时间都是 20
'c' 按字母顺序排列比 'b' 大,所以答案是 'c'
示例 2:
输入:releaseTimes = [12,23,36,46,62], keysPressed = "spuda"
输出:"a"
解释:按键顺序和持续时间如下:
按下 's' ,持续时间 12
按下 'p' ,持续时间 23 - 12 = 11
按下 'u' ,持续时间 36 - 23 = 13
按下 'd' ,持续时间 46 - 36 = 10
按下 'a' ,持续时间 62 - 46 = 16
按键持续时间最长的键是 'a' ,持续时间 16
class Solution {
public char slowestKey(int[] releaseTimes, String keysPressed) {
int maxTime = releaseTimes[0]; // 第一个字符
char ans = keysPressed.charAt(0); // 第一个数 就是第一个字符的持续时间
for (int i = 1; i < keysPressed.length(); i++) {
// 当前字符的持续时间
int time = releaseTimes[i] - releaseTimes[i-1];
// 当前字符
char ch = keysPressed.charAt(i);
// 当前按键持续时间大于按键持续的最长时间;
// 当前按键持续时间等于按键持续的最长时间 且 字符的排序大于前一个字符。a(97) < b(98) < c(99) < d(100)
if (time > maxTime || (time == maxTime && ch > ans)) {
ans = ch;
maxTime =time;
}
}
return ans;
}
}
27. 移除链表元素 原题
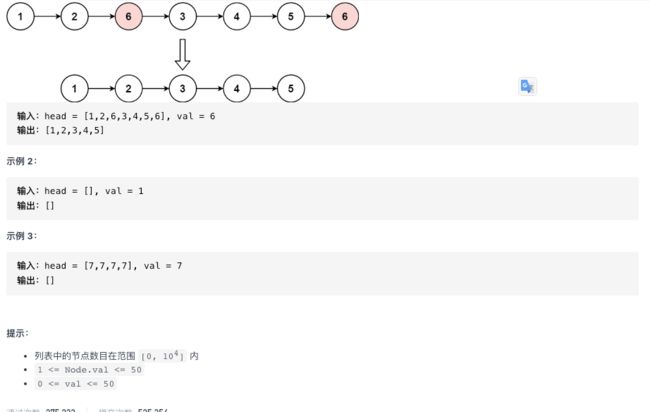
给你一个链表的头节点 head 和一个整数 val ,
请你删除链表中所有满足 Node.val == val 的节点,并返回 新的头节点 。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeElements(ListNode head, int val) {
// 使用双节点
/**
if (head == null) return null;
// 定一个虚拟的头节点 指向 head 列表
ListNode temp = new ListNode(-1,head);
ListNode curNode = head; //定义一个指针 指向这个有虚拟头节点的链表
ListNode preNode =temp; // 定义一个前节点的指针,指向虚拟头节点
//
while (curNode != null) {
if (curNode.val == val) {
//找到需要删除的节点 将前一个节点的指针指向当前节点的下一个节点,表示删除该节点
preNode.next = curNode.next;
}else {
// 不是要删除的节点,把当前的节点赋值给前一个节点
preNode = curNode;
}
// 当前节点向后移动
curNode = curNode.next;
}
return temp.next;
*/
// 使用本身的链表
if (head != null && head.val == val) {
head = head.next;
}
if (head == null) return head;
//ListNode preNode = head;
ListNode curNode = head;
while (curNode.next != null) {
if (curNode.next.val == val) {
curNode.next = curNode.next.next;
}else{
curNode = curNode.next;
}
}
return head;
}
}
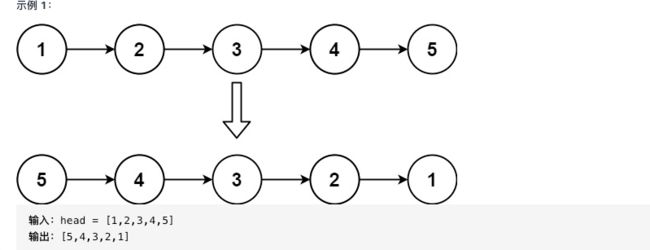
28.反转链表 原题
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode reverseList(ListNode head) {
ListNode preNode = null; // 前指针
ListNode curNode = head; // 当前指针
ListNode tempNode = null; // 临时节点
while (curNode != null) { // 当前节点不为空的时候,把当前节点指向前一个节点
tempNode = curNode.next; // 存放下一个节点
curNode.next = preNode; // 当前节点 指向 前一个节点
preNode = curNode; // 前节点==当前节点,前节点后移
curNode = tempNode; // 当前节点 == 下一个节点。当前节点后移
}
return preNode;
}
}
29.两两交换链表中的节点原题
给你一个链表,两两交换其中相邻的节点,并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题(即,只能进行节点交换)。
输入:head = [1,2,3,4]
输出:[2,1,4,3]
示例 2:
输入:head = []
输出:[]
示例 3:
输入:head = [1]
输出:[1]
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode swapPairs(ListNode head) {
if (head == null || head.next == null) return head;
ListNode virtalNode = new ListNode(0,head);
ListNode curNode = virtalNode; // 定义虚拟头节点
// 只有在后面两个节点都不为null 的时候才能互换
while (curNode.next != null && curNode.next.next != null) {
ListNode temp = head.next.next; // 存放第三个节点
curNode.next = head.next; // 虚拟头 的下一个节点为 head的下一个节点。curNode-> 2
head.next.next = head; // head的第二个节点的下一个指向head节点。 2->1
head.next = temp; // head 指向 第三个节点。 1-> 3
curNode =head; // curNode 移动到head curNOde - 1
head = head.next; // head 移动到下一个 virtual ->2 ->1 -> 3 -> 4
//curNode head
}
return virtalNode.next;
}
}
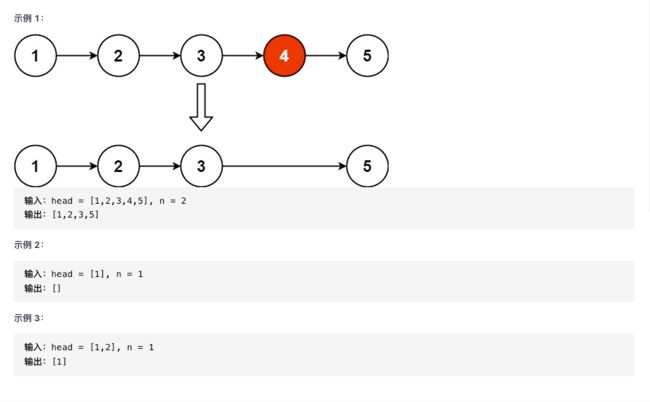
30. 删除链表的倒数第 N 个结点 原题
给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点
- 定义一个虚拟头节点让其指向head
- 定义两个指针, 一个fast 一个low
- fast 先走 n 步,走到待删节点的前一个节点,然后fast 和 low 一个向后走,fast 和 low 相差 n 步
- 当 fast 为null 时 low 节点指向了待删除节点的前一个节点,然后进行删除。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode virtual = new ListNode(0,head); // 定义一个虚拟头节点
ListNode fast = head; // 定义一个快指针 让其先走 n 步
ListNode low = virtual; // 定义一个满指针 指向虚拟头
// 让 fast先走n步此时fast指向待删节点的前一个节点
for (int i = 0; i < n; i++){
fast = fast.next;
}
// 让 fast 和 low 一起往后走,当 fast 为空的时候,low 指向待删除节点的前一个节点
while (fast != null) {
fast = fast.next;
low = low.next;
}
// 删除节点
low.next = low.next.next;
return virtual.next;
}
}
思路二
- 定义一个虚拟节点指向head
- 定义一个方法来获取链表的长度
- 让该长度 减去 n,就是链表需要走的长度,可以正好走到待删接节点的前一个节点,
- 然后进行删除操作
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
ListNode virtual = new ListNode(0,head);
ListNode curNode = virtual;
int length = getLength(head);
for (int i = 1; i < length - n ; i++) {
curNode = curNode.next;
}
curNode.next = curNode.next.next;
return virtual.next;
}
public int getLength(ListNode head){
if (head == null) return 0;
int res = 0;
ListNode tmp = head;
while (tmp != null){
tmp = tmp.next;
res++;
}
return res;
}
}
31. 链表相交原题
节点相同
给你两个单链表的头节点 headA 和 headB ,
请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点,返回 null 。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode curNodeA = headA;
ListNode curNodeB = headB;
/**
两个链表 A 和 B 如果有相交节点那么 遍历完两个链表的最后就会有相同的节点
没有相交的节点,遍历完两个链表最后 curNodeA和curNodeB 都是null 直接返回。
A: 1 -3 -4 -5 -6
B: 2 -7 -8 -5 -6
遍历两个链表 A+B
A : 1-3-4-5-6- 2-7-8-5-6
B : 2-7-8-5-6- 1-3-4-5-6
最后会有相同的节点,直接返回 curNodeA或者curNodeB
当 A B 没有相交的节点。 curNodeA和curNodeB 都是null 直接返回。
*/
while (curNodeA != curNodeB) {
curNodeA = curNodeA == null ? headB : curNodeA.next;
curNodeB = curNodeB == null ? headA : curNodeB.next;
}
return curNodeA;
}
}
思路二
- 获取两个链表的长度
- 让长度长的链表始终是A:当B的长度大于A 的时, 交换链表指针,并获取长度的差值n。并让A 向后移动差值n 步,让链表A ,B 保持相同的长度
- 开始向后遍历链表A B 当两个链表有相同的节点时(headA == headB)时直接返回链表A,否则一直向后遍历。直到 A B 值为null 表示没有相交的节点点并返回链表A
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
ListNode curNodeA = headA;
ListNode curNodeB = headB;
// 获取两个链表的长度,我们始终让链表A为 最长的链表
int lengthA = getLength(headA);
int lengthB = getLength(headB);
int num = lengthA - lengthB; // 长度差值 表示 A需要向后移动多少步
// 当链表B的长度大于A时,那没就让A B 互换,保持A为最长的链表
if (lengthB > lengthA) {
ListNode tmp = curNodeA;
curNodeA = curNodeB;
curNodeB = tmp;
num = lengthB - lengthA; // 并跟新长度差值
}
// 让A 向后移动差值的步数
for (int i =0;i < num;i++) {
curNodeA = curNodeA.next;
}
// A B 此时的长度相等,并同时向后移动
// 当其中有节点相等时直接返回该节点,否则返回null;
while (curNodeA != null) {
if (curNodeA == curNodeB) return curNodeA;
curNodeA = curNodeA.next;
curNodeB = curNodeB.next;
}
return null;
}
// 获取链表长度
public int getLength(ListNode head){
if (head == null) return 0;
int num = 0;
ListNode tmp = head;
while (tmp != null) {
tmp = tmp.next;
num++;
}
return num;
}
}
32. 有效的字母异位词。 原题
-
字母异位词: 两个单词包含相同的字母,但是次序不同
-
将字母排好序,在比较是否相同
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。
注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。
示例 1:
输入: s = “anagram”, t = “nagaram”
输出: true
示例 2:输入: s = “rat”, t = “car”
输出: false提示:
1 <= s.length, t.length <= 5 * 104
s 和 t 仅包含小写字母
class Solution {
public boolean isAnagram(String s, String t) {
// 字母异位词: 两个单词包含相同的字母,但是次序不同
// 将字母排好序,在比较是否相同
// 1、将两个字符串转为 char数组
char[] sArray = s.toCharArray();
char[] tArray = t.toCharArray();
// 2、将两个char数组从小到大排序
Arrays.sort(sArray);
Arrays.sort(tArray);
// 3、比较两个排序好的char数组是否相同
return Arrays.equals(sArray,tArray);
}
}
33. 两个数组的交集 原题
给定两个数组,编写一个函数来计算它们的交集。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2]
示例 2:
输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[9,4]
说明:
输出结果中的每个元素一定是唯一的。
我们可以不考虑输出结果的顺序。
class Solution {
public int[] intersection(int[] nums1, int[] nums2) {
// 暴力解
// 输出结果中的每个元素一定是唯一的。使用set 集合
// 我们可以不考虑输出结果的顺序。
Set<Integer> set = new HashSet();
for (int i = 0; i < nums1.length; i++) {
for (int j = 0; j < nums2.length; j++) {
if (nums1[i] == nums2[j]) {
set.add(nums1[i]);
continue;
}
}
}
// 将set集合转为数组
int[] res = new int[set.size()];
int index = 0;
for (int i : set){
res[index++] = i;
}
return res;
}
}