光学成像模型\和物距、像距、焦距、三者关系\和世界坐标、相机坐标、图像坐标、像素坐标关系\和图像畸变标定处理（二）

来自百度百科：https://zhidao.baidu.com/question/55907940.html
原文链接：https://blog.csdn.net/qq_35250841/article/details/106198870
原文链接：/blog.csdn.net/weixin_44523062/category_9977613.html

零、小孔成像模型

一、凸透镜，物距、像距、焦距、三者关系

物距为u，像距为v，焦距为f，三者的关系为：1/v +1/u=1/f。

根据该关系，不同的物距、像距、焦距的关系使得成像特点不同：

1、当物距大于2倍焦距时，则像距在1倍焦距和2倍焦距之间，成倒立、缩小的实像。此时像距小于物距，像比物小，物像异侧。应用：照相机、摄像机。

2、当物距等于2倍焦距时，则像距也在2倍焦距， 成倒立、等大的实像。此时物距等于像距，像与物大小相等，物像异侧。应用：测焦距。

3、当物距小于2倍焦距、大于1倍焦距时，则像距大于2倍焦距， 成倒立、放大的实像。此时像距大于物距，像比物大，物像异侧。应用：投影仪、幻灯机、电影放映机。

4、当物距等于1倍焦距时，则不成像，成平行光射出。

5、当物距小于1倍焦距时，则成正立、放大的虚像。此时像距大于物距，像比物大，物像同侧。应用：放大镜。

二、凸透镜光学成像模型

最上面一条从物体发出并平行于透镜的光轴，经过透镜折射后穿过另一侧的焦点。

第二条光束穿过透镜左侧的焦点，经过折射，与光轴平行。

第三条光束直接穿过透镜中心。因为透镜垂直于主光轴并且厚度很小，当光透过其中心时，折射可以忽略不计。

其中 u 为物距， f 为焦距，v 为相距。三者满足关系式：

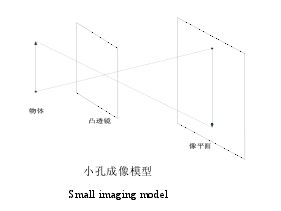
三、相机小孔成像模型
相机的镜头是一组透镜，当平行于主光轴的光线穿过透镜时，会聚到一点上，这个点叫做焦点，焦点到透镜中心的距离叫做焦距 f。数码相机的镜头相当于一个凸透镜，感光元件就处在这个凸透镜的焦点附近，将焦距近似为凸透镜中心到感光元件的距离时就成为小孔成像模型。小孔成像模型如图所示。

四、相机模型四个坐标系

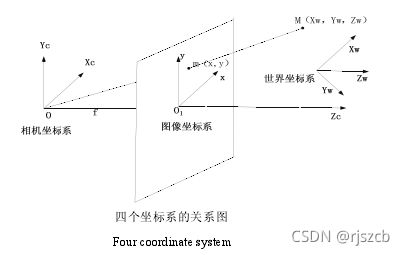
	数码相机图像拍摄的过程实际上是一个光学成像的过程。相机的成像过程涉及到四个坐标系：

世界坐标系、相机坐标系、图像坐标系、像素坐标系以及这四个坐标系的转换。

①世界坐标系：是客观三维世界的绝对坐标系，也称客观坐标系。因为数码相机安放在三维空间中，我们需要世界坐标系这个基准坐标系来描述数码相机的位置，并且用它来描述安放在此三维环境中的其它任何物体的位置，用（Xw, Yw, Zw）表示其坐标值。

②相机坐标系（光心坐标系）：以相机的光心为坐标原点，X 轴和Y 轴分别平行于图像坐标系的 X 轴和Y 轴，相机的光轴为Z 轴，用（Xc, Yc, Zc）表示其坐标值。

③图像坐标系：以CCD 图像平面的中心为坐标原点，X轴和Y 轴分别平行于图像平面的两条垂直边，用( x , y )表示其坐标值。图像坐标系是用物理单位（例如毫米）表示像素在图像中的位置。

④像素坐标系：以 CCD 图像平面的左上角顶点为原点，X 轴和Y 轴分别平行于图像坐标系的 X 轴和Y 轴，用(u , v )表示其坐标值。数码相机采集的图像首先是形成标准电信号的形式，然后再通过模数转换变换为数字图像。每幅图像的存储形式是M × N的数组，M 行 N 列的图像中的每一个元素的数值代表的是图像点的灰度。这样的每个元素叫像素，像素坐标系就是以像素为单位的图像坐标系

1）、模型一
四个坐标系的关系图如下图所示，其中 M 为三维空间点，m 为 M 在图像平面投影成的像点。

2）、模型二
四个坐标系的关系图如下图所示，其中 M 为三维空间点，m 为 M 在图像平面投影成的像点。

3）、模型三
四个坐标系的关系图如下图所示，其中 P 为三维空间点，p 为 P 在图像平面投影成的像点。

4）、模型四
四个坐标系的关系图如下图所示，其中 P 为三维空间点，p 为 P 在图像平面投影成的像点。真实世界中的空间点
Pw(Xw， Yw， Zw)， 其对应的相机坐标系坐标为Pc(Xw， Yw， Zw）， 对应的图像坐标
系坐标为P(x ,y),对应的像素坐标为p(u， v）。

五、像素坐标系与图像坐标系

他们间的转换公式，其中（u0, v0）是图像坐标系原点在像素坐标系中的坐标，dx 和 dy分别是每个像素在图像平面x和 y方向上的物理尺寸。

1、采用齐次坐标再用矩阵形式将上式表示为

2、也可以写成下面


六、图像坐标系与相机坐标系

其中 f 为焦距（像平面与相机坐标系原点的距离）。用齐次坐标系和矩阵表示上述关系：

七、相机坐标系与世界坐标系
相机坐标系与世界坐标系的变换为：

其中 R 为3 × 3正交旋转矩阵，t 为三维平移向量，综合起来：

ax, ay分别是图像水平轴和垂直轴的尺度因子。K的参数中只包含焦距、主点坐标等只由相机的内部结构决定，因此称 K 为内部参数矩阵，ax, ay , u0, v0叫做内部参数。M1中包含的旋转矩阵和平移向量是由相机坐标系相对于世界坐标系的位置决定的，因此称M1为相机的外部参数矩阵，R和t叫做外部参数，M 叫投影矩阵。相机标定就是确定相机的内部参数和外部参数。

也可以写成下面的公式。

八、畸变标定

实际成像模型
理想的透视模型是针孔成像模型，物和像会满足相似三角形的关系。但是实际上由于相机光学系统存在加工和装配的误差，透镜就并不能满足物和像成相似三角形的关系，所以相机图像平面上实际所成的像与理想成像之间会存在畸变。畸变属于成像的几何失真，是由于焦平面上不同区域对图像的放大率不同形成的画面扭曲变形的现象，这种变形的程度从画面中心至画面边缘依次递增，主要在画面边缘反映比较明显。为了减小畸变，拍摄图片时应尽量避免用镜头焦距的最广角端或最远端拍摄。实际的相机成像模型如下图所示。

其中 mr(xr,yr)表示实际投影点的像平面坐标系下的物理坐标，mi(xi,yi)表示理想投影点的像平面坐标系下的物理坐标。镜头的畸变模型可表示为：

σx 和σy是非线性畸变值，它包括径向畸变和偏心畸变和薄棱镜畸变等。
理论上来说镜头都存在径向和切向畸变，但是通常径向畸变较大，切向畸变较小。径向畸变的模型可由下面的模型来表示：

其中k1 k2 k3……示径向畸变系数，，通常情况下径向畸变系数只考虑到一阶或二阶就可以满足精度需求了。
偏心畸变模型是由于多个光学镜头的光轴不能完全共线产生的，这种畸变是由径向和切向畸变共同构成的，数学模型可表示如下：

其中p1, p2为切向畸变系数。薄棱镜畸变是由于镜头设计制造缺陷和加工安装所造成的，如镜头与相机成像平面有一个很小的倾角等。因为薄棱镜畸变非常小，通常不考虑，这里只考虑径向畸变和偏心畸变，畸变总的可以表示为：

实际的成像模型为：

下面的是另一个博客参考的，感觉不是这样，我实际开发项目用的模型是上面的，采用opcv库，MATLAB获取标定参数（下章节将讲到如何标定，畸变校正）

，但是公式可以参考一下。
上面推导了相机投影成像的数学模型， 这是在理想状况下推导的， 实际上由于相机
光学系统存在加工和装配的误差， 透镜就并不能满足物和像成相似三角形的关系， 所以
相机图像平面上实际所成的像与理想成像之间会存在畸变。 畸变属于成像的几何失真，
是由于焦平面上不同区域对图像的放大率不同形成的画面扭曲变形的现象， 这种变形的
程度从画面中心至画面边缘依次递增， 主要在画面边缘反映比较明显。
相机的畸变可以由非线性模型来表示， 由于公式比较复杂， 对于推导过程， 此处将
不再赘述， 最后给出简化后的畸变模型：

其中(X,Y,Z)为世界坐标系下的坐标， (x,y,x)为相机坐标系下的坐标， 归一化为(x’,y’)，
(x’’,y’’)为加入畸变参数的归一化坐标， (u,v)为畸变模型下的像素坐标。݇K1, ݇2, ݇3, ݇4, ݇5, ݇6,为 径向畸变参数， ݌1, ݌2为切向畸变参数。