LeetCode刷题--热题Hot100
热题 Hot 100
1. 两数之和
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
// 双重for循环,时间复杂度O(n^2)
func twoSum(nums []int, target int) []int {
var i,j int
res := make([]int, 0)
// for i, num := range nums {
for i=0;i//使用哈希表,可以将寻找 target - num 的时间复杂度降低到从 O(N) 降低到 O(1)。
func twoSum(nums []int, target int) []int {
hashTable := map[int]int{}
for i,num := range nums {
targetNum := target-num
if targetNumIndex, ok := hashTable[targetNum];ok {
return []int{targetNumIndex, i}
} else {
hashTable[num] = i
}
}
return nil
}2. 两数相加
给你两个非空的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储一位数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
方法一:模拟
思路与算法
由于输入的两个链表都是逆序存储数字的位数的,因此两个链表中同一位置的数字可以直接相加。
我们同时遍历两个链表,逐位计算它们的和,并与当前位置的进位值相加。具体而言,如果当前两个链表处相应位置的数字为 n1,n2,进位值为carry,则它们的和为 n1+n2+carry;其中,答案链表处相应位置的数字为 (n1+n2+carry)mod10,而新的进位值为 (n1+n2+carry)/10
如果两个链表的长度不同,则可以认为长度短的链表的后面有若干个 0 。
此外,如果链表遍历结束后,有carry>0,还需要在答案链表的后面附加一个结点,结点的值为 carry。
func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode {
//定义一个头结点和尾结点,尾结点或者可以理解为临时结点
var head, tail *ListNode
// 定义一个进位数carry,carry为几就说明要进位多少
carry := 0
//依次遍历两个链表,只要元素不为空就进行下一步
for l1 != nil || l2 != nil {
//定义两个变量存储各个结点的值
n1, n2 := 0,0
// 从第一个链表开始
if l1 != nil {
// 把每个结点的值赋给n1
n1 = l1.Val
// 结点后移
l1 = l1.Next
}
// l2同上
if l2 != nil {
// 把每个结点的值赋给n1
n2 = l2.Val
// 结点后移
l2 = l2.Next
}
// 此时是两个链表第一个元素的和 + 进位数
sum := n1 + n2 + carry
//sum%10是结点的当前值,如果是10,取余后当前结点值为0,sum/10是求十位的那个数
//存入的结果为a+b+进位数,再对10取余
// 计算进位值carry
sum,carry = sum%10,sum/10
// 此时申请一个新的链表存储两个链表的和
//申请新的链表
if head == nil{
//申请新的链表
head = &ListNode{Val:sum}
//这一步是为了保持头结点不变的情况下指针可以右移,所以说tail相当于临时结点,理解成尾结点也可以,
//因为此时新链表中只有一个结点,所以头结点和尾结点都指向同一个元素。
tail = head
} else {
//第二个结点后开始逐渐往尾结点增加元素
tail.Next = &ListNode{Val:sum}
tail = tail.Next
}
}
//把最后一位的余数加到链表最后
if carry > 0 {
tail.Next = &ListNode{Val:carry}
}
return head
}3. 无重复字符的最长子串
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
方法一:暴力解法
逐个生成子字符串
看它是否不含有重复的字符
外层for循环遍历起始字符,内层for循环遍历终止字符
对于每个子串,再次遍历它是否含有重复字符 hash set O(n) 双指针O(n^2)
方法二:滑动窗口及优化
重复字符--> 出现1次
模式识别1:一旦涉及出现次数,需要用到散列表
构造子串,散列表存下标
模式识别2:涉及字串,考虑滑动窗口
我们使用两个指针表示字符串中的某个子串(或窗口)的左右边界,其中左指针代表着上文中「枚举子串的起始位置」,而右指针即为上文中的 rk;
在每一步的操作中,我们会将左指针向右移动一格,表示 我们开始枚举下一个字符作为起始位置,然后我们可以不断地向右移动右指针,但需要保证这两个指针对应的子串中没有重复的字符。在移动结束后,这个子串就对应着 以左指针开始的,不包含重复字符的最长子串。我们记录下这个子串的长度;
在枚举结束后,我们找到的最长的子串的长度即为答案。
在左指针向右移动的时候,我们从哈希集合中移除一个字符,在右指针向右移动的时候,我们往哈希集合中添加一个字符。
func lengthOfLongestSubstring(s string) int {
// 哈希集合,记录每个字符是否出现过
m := make(map[string]int, 0)
n := len(s)
// 右指针,初始值为-1,相当于我们在字符串的左边界的左侧,还没有开始移动
rk, ans := -1, 0
for i := 0; i < n; i++ {
if i!=0 {
// 左指针向右移动一格,移除一个字符
delete(m, s[i-1])
}
if (rk +1 < n&& m[s[rk+1]] == 0) {
// 不断地移动右指针
m[s[rk+1]]++
rk++
}
// 第i到rk个字符是一个极长的无重复字符字串
ans = max(ans, rk-i+1)
}
return ans
}4. 寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
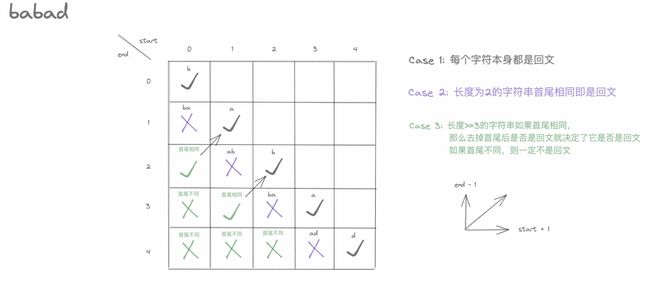
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
分析步骤
1. 怎么判断一个字符串是否是回文,可以归纳为哪几种形式?
比较容易想到,对于回文我们可以归纳为三种case,分别是:
一个字符本身就是回文
长度为2的字符串首尾相同就是回文
长度>2如果首尾相同,那么去掉首尾后是否是回文就决定了它是否是回文;
如果首尾不同,则一定不是回文
2. 选用哪种算法解题?
抛去前两种case,第三种case是典型的的可以使用动态规划解题的特征。即后面的判断可以以前面的结算结果作为依据。
3. 画图分析
4. 代码怎么写
动态规划初始数据的初始化
遍历方向,对应图中的操作就是如何填满剩余空格,这里有两种选择:
纵向填充,即起点固定,不断延长长度
对角填充,即长度固定,不断移动起点
结合图示可以比较直观的想到,纵向填充会遇到状态转移时所依赖的前置数据还没有计算到的问题,所以选择对角填充。
记录最大值
func longestPalindrome(s string) string {
len := len(s)
if (len < 2) {
return s
}
maxLen, begin := 1, 0
// dp[i][j]表示s[i..j]是否是回文串
dp := make([][]bool,len)
// result := s[0:1] //初始化结果(最小的回文就是单个字符)
// 初始化:所有长度为1的子串都是回文串
for i:=0;i= len) {
break
}
if (s[i] != s[j]) { //首尾不同则不可能为回文
dp[i][j] = false
} else {
if (j-i<3) {
dp[i][j] = true
} else {
dp[i][j] = dp[i+1][j-1]
}
}
//只要dp[i][L] == true成立,就表示子串s[i..L]是回文,此时记录回文长度和起始位置
if (dp[i][j] && j-i+1 > maxLen) { //记录最大值
maxLen = j-i+1
begin = i
result = s[begin:begin + maxLen]
}
}
}
return s[begin:begin + maxLen]
// return result
} 10. 正则表达式匹配
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。
func isMatch(s string, p string) bool {
m, n := len(s), len(p)
f := make([][]bool,m+1)
for i:=0;i19. 删除链表的倒数第 N 个结点
golang 快慢双指针,创建一个ListNode end节点的next指向head节点,定义快慢指针指向end,先让fast指针走n次,这样slow节点与fast节点之间相差n个节点,之后再同步走 即可保证slow.next是要删除的节点
/**
* Definition for singly-linked list.
* type ListNode struct {
* Val int
* Next *ListNode
* }
*/
func removeNthFromEnd(head *ListNode, n int) *ListNode {
end := &ListNode{}
end.Next = head
fast := end // 快指针
slow := end // 慢指针
for i:=0;i22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
思想:回溯+剪枝
画图
画图以后,可以分析出的结论:
当前左右括号都有大于 0 个可以使用的时候,才产生分支;
产生左分支的时候,只看当前是否还有左括号可以使用;
产生右分支的时候,还受到左分支的限制,右边剩余可以使用的括号数量一定得在严格大于左边剩余的数量的时候,才可以产生分支;
在左边和右边剩余的括号数都等于 0 的时候结算。
func generateParenthesis(n int) []string {
res := new([]string)
// 特判
if n == 0 {
return *res
}
// 执行深度优先遍历,搜索可能的结果
dfs("", n, n, res)
return *res
}
// @param curStr 当前递归得到的结果
// @param left 左括号还有几个可以使用
// @param right 右括号还有几个可以使用
// @param res 结果集
func dfs(curStr string, left int, right int, res *[]string) {
// 因为每一次尝试,都使用新的字符串变量,所以无需回溯
// 在递归终止的时候,直接把它添加到结果集即可
// if left == 0 && right == 0 {
if right == 0 {
//并不需要判断左括号是否用完,因为右括号生成的条件 right > left
*res = append(*res, curStr)
return
}
// 剪枝(如图,左括号可以使用的个数严格大于右括号可以使用的个数,才剪枝,注意这个细节)
// if left > right {
// return
// }
if left > 0 {
dfs(curStr+"(", left-1, right, res)
}
// if right > 0 {
// dfs(curStr+")", left, right-1, res)
// }
// 括号成对存在,有左括号才会有右括号
if right > left {
dfs(curStr+")", left, right-1, res)
}
}