算法刷题笔记-hot100-1-10(进行中)
文章目录
-
- [1. 两数之和](https://leetcode.cn/problems/two-sum/)
-
- 题意
- 题解
- [2. 两链表数相加](https://leetcode.cn/problems/add-two-numbers/)
-
- 题意
- 题解
-
- 方法1:不使用虚拟头节点
- 方法2:代码优化:使用虚拟头节点
- [3. 无重复字符的最长子串](https://leetcode.cn/problems/longest-substring-without-repeating-characters/)
-
- 题意
- 题解
- [4. 寻找两个正序数组的中位数](https://leetcode.cn/problems/median-of-two-sorted-arrays/)
-
- 题意
- 题解
- 复杂度
1. 两数之和
题意
-
给定一个整数数组 nums 和一个整数目标值 target,
- 请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
-
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
-
你可以按任意顺序返回答案。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
题解
class Solution {
public int[] twoSum(int[] nums, int target) {
HashMap<Integer, Integer> map = new HashMap();// 反向表-值->下标
for(int i = 0; i < nums.length; i ++) {
if(map.containsKey(target - nums[i])) {
return new int[] {i, map.get(target - nums[i])};
} else {
map.put(nums[i], i);
}
}
return new int[] {-1, -1};
}
}
2. 两链表数相加
题意
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
输入:l1 = [2,4,3], l2 = [5,6,4]
输出:[7,0,8]
解释:342 + 465 = 807.
示例 2:输入:l1 = [0], l2 = [0]
输出:[0]
示例 3:输入:l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
题解
方法1:不使用虚拟头节点
- 要先处理好头节点的值
- 这样,才能在循环中,将链表串起来
- 注意:最后一个进位要加上
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
boolean add1 = false; // 判断是否需要进位1
// 先处理好第一个节点
int n1 = l1.val; // 第一个链表节点val
int n2 = l2.val; // 第二个链表节点val
int r = add1 ? 1: 0; // 进位数-0或1
int n = n1 + n2 + r; // 累加的值
add1 = (n >= 10) ? true : false;
ListNode res = new ListNode(n % 10);
ListNode cur1 = l1.next;
ListNode cur2 = l2.next;
ListNode head = res;
ListNode newCur = null; // 每个节点都需要新建
// 处理最长链表长度的节点
while(cur1 != null || cur2 != null) {
n1 = cur1 != null ? cur1.val : 0;
n2 = cur2 != null ? cur2.val : 0;
r = add1 ? 1 : 0;
n = n1 + n2 + r;
add1 = (n >= 10) ? true : false;
newCur = new ListNode(n % 10);
head.next = newCur;
// 进行下轮循环
head = newCur;
cur1 = cur1 != null ? cur1.next : null;
cur2 = cur2 != null ? cur2.next : null;
}
// 处理进位后的最后一个节点
if(add1) {
head.next = new ListNode(1);
}
return res;
}
}
方法2:代码优化:使用虚拟头节点
- 1.创建一个虚拟头节点,头节点逻辑一块处理,最后返回虚拟头节点的下个节点即可
- 2.可以省去判断是否进位的布尔变量,与10整除的商即是要进位的0或1
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
int n1 = 0; // 第一个链表节点val
int n2 = 0; // 第二个链表节点val
int r = 0; // 进位数-0或1
int n = 0; // 累加的值
ListNode cur1 = l1;
ListNode cur2 = l2;
ListNode pre = new ListNode(1); // 虚拟头节点
ListNode resPre = pre;
ListNode newCur = null; // 每个节点都需要新建
// 处理最长链表长度的节点
while(cur1 != null || cur2 != null) {
n1 = cur1 != null ? cur1.val : 0;
n2 = cur2 != null ? cur2.val : 0;
n = n1 + n2 + r;
r = n / 10; // 商即是进位
newCur = new ListNode(n % 10);
pre.next = newCur;
// 进行下轮循环
pre = newCur;
cur1 = cur1 != null ? cur1.next : null;
cur2 = cur2 != null ? cur2.next : null;
}
// 处理进位后的最后一个节点
if(r == 1) {
pre.next = new ListNode(1);
}
return resPre.next;
}
}
3. 无重复字符的最长子串
题意
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
示例 2:输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”,所以其长度为 1。
示例 3:输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”,所以其长度为 3。
请注意,你的答案必须是 子串 的长度,“pwke” 是一个子序列,不是子串。
题解
-
1.涉及到子串问题,可以从子串最后一个字符着手,而不是第一个字符处理
- 如果从第一个字符处理,后面字符会重复验证处理
- 反之,从后往前查找,只需在前面验证过的字符做好标记,无需重复验证,
- 并且可以使用之前元素处理的结果
-
2.建立反序表,通过字符反向查找索引位置,可以用数组代替哈希表,提高性能
-
3.为确定字串最后一个字符的左边界,设定两个指标:
- 指标1:与当前字符重复的字符位置
- 指标2:前一个字符往左推的最远位置-可以完全使用之前处理过的验算,提高性能
class Solution {
public int lengthOfLongestSubstring(String s) {
// 一定要先处理好特殊边界
if(s == null || s.length() == 0) {
return 0;
}
char[] arr = s.toCharArray();
// 建立反序表-字符->下标位置
int[] temp = new int[256]; // 下标为字符的ASCII码
for(int i = 0; i < 256; i ++) {
temp[i] = -1; // 初始都在0位置左边
}
int preIndex = -1; // 末字符的前一个字串左边界(开)
int res = -1; // 无重复字符的子串长度
for(int i = 0; i < arr.length; i ++) {
// 指标1:与当前字符重复的字符位置
// 指标2:前一个字符往左推的最远位置
// 取两个指标位置最近的,作为当前子串的左边界(开)
preIndex = Math.max(temp[arr[i]], preIndex);
res = Math.max(res, (i - preIndex));
temp[arr[i]] = i; // 更新反序表-字符回自动转为int类型的ASCII码
}
return res;
}
}
4. 寻找两个正序数组的中位数
题意
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。
请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/median-of-two-sorted-arrays
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
题解
-
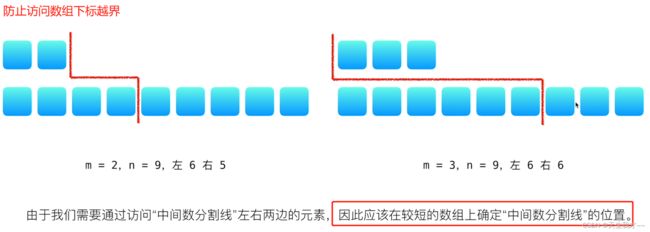
==1.中位数,主要确定数组的分割线位置,使用二分查找确定==
-
2.两个指标:
- 指标1:i + j = (m + n + 1) / 2
- 指标2:nums1[i-1]<=nums2[j] && nums2[j-1]<=nums1[i]
- 因此,只需找到一个数组的分割线,另一个分割线根据1确定
- 3.注意边界处理:
- 4.通过边界、奇偶分别处理
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
/* 1. 为简化边界条件,设置数组1为短,数组2为长数组*/
if(nums1.length > nums2.length) {
int[] tmp = nums1;
nums1 = nums2;
nums2 = tmp;
}
/* 2. 使用二分法划分分割线-找分割线右边位置i,j
指标1:i + j = (m + n + 1) / 2
指标2:nums1[i-1]<=nums2[j] && nums2[j-1]<=nums1[i]
因此,只需找到一个数组的分割线,另一个分割线根据1确定
*/
int m = nums1.length;
int n = nums2.length;
int left = 0;
int right = m;
int sumLeft = m + (n - m + 1) / 2; // 指标1:分割线左总数
int i, j; // 两数组在分界线右边的第一个位置
// 也分别是两数组分割线左边元素个数
while(left < right) { // 通过数组1的指标2二分查找
i = left + (right - left + 1) / 2; // 找中,向下取整
j = sumLeft - i;
if(nums1[i - 1] > nums2[j]) { // 数组1边界靠右了
right = i - 1; // [left, i - 1]
} else { // 将数组2满足与否都包含
// [left,right],防止死循环,故,i要向下取整,一定能进1,且i-1边界一定满足
left = i;
}
}
/* 3. 根据边界确定中位数-奇偶区分
如果是奇数,边界左边最大的数是唯一中位数
如果是偶数,边界左边最大是上中位数,边界右边最小是下中位数,取平均值
注意,边界条件,一个数组的边界左边为null,或边界右边为null,不能参与竞争
*/
i = left;
j = sumLeft - i;
int nums1LeftMax = i - 1 < 0 ? Integer.MIN_VALUE : nums1[i - 1]; // 数组1边界左最大
int nums1RightMin = i >= m ? Integer.MAX_VALUE : nums1[i]; // 数组1边界右最小
int nums2LeftMax = j - 1 < 0 ? Integer.MIN_VALUE : nums2[j - 1]; // 数组2边界左最大
int nums2RightMin = j >= n ? Integer.MAX_VALUE : nums2[j]; // 数组2边界右最小
if((n + m) % 2 == 1) { // 奇数
return Math.max(nums1LeftMax, nums2LeftMax);
} else { // 偶数
return (double) ((Math.max(nums1LeftMax, nums2LeftMax) + Math.min(nums1RightMin, nums2RightMin))) / 2;// 要先转double再除以2
}
}
}