LeetCode287.寻找重复数

LeetCode287.寻找重复数

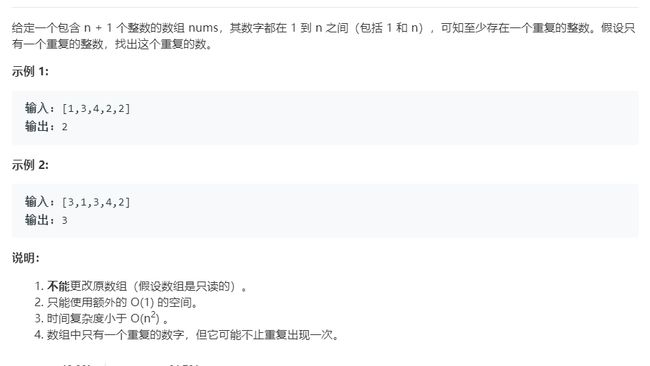
题目描述

思路

不加限制：

• 使用哈希表判重，违反限制2
• 将原始数组排序，找排序后重复的数相邻，违反规则1
• 类似LeetCode41：原地哈希的思路，当两个数发现要放到同一个地方时就发现此元素，但是违反限制1

不考虑说明（即不考虑额外空间的限制）

​ 要是不考虑额外空间的限制，直接引入一个SetHash来保存数组，遇到没遇到过的就放进去，遇到遇到过的就直接弹出

考虑说明

二分查找

​ 既然要定位数，这个数恰好是一个整数，可以在[整数的有效范围内]做二分查找，但是比较烦的一点就是反复查看数组好几次。

• 由于题目中有很多有利条件：查找的数是一个整数，并且给出这个整数的范围。于是可以使用二分查找定位在一个区间里的整数
• 思想是先猜一个数（有效范围【left，right】里面的中间数mid），然后统计原始数组中小于等于这个中间数的元素的个数cnt。如果cnt严格大于mid。那么根据抽屉原理就在其中。
• 此方法是空间敏感的，即以时间换空间。

快慢指针

​ 需要对【Floyd判圈算法】（龟兔赛跑算法）

​ 我们对nums[]数组建图，每个位置i连一条i→nums[i]的边，由于存在重复数字target，因此整张图一定存在环，我们要找到的target就是这个环的入口。

​ 我们先设置慢指针slow和快指针fast，慢指针每次走一步，快指针每次走两步。根据【Floyd判圈算法】两个指针在有环的情况下一定会相遇。

​ 此时我们再将slow放置在起点0.两个指针每次同时移动一步，相遇的点就是答案

解释：

​ 假设环长为 L，从起点到环的入口的步数是 a，从环的入口继续走 b 步到达相遇位置，从相遇位置继续走 c 步回到环的入口，则有 b+c=L，其中 L、a、b、c 都是正整数。

​ 根据上述定义，慢指针走了 a+b 步，快指针走了 2(a+b)步。从另一个角度考虑，在相遇位置，快指针比慢指针多走了若干圈，因此快指针走的步数还可以表示成 a+b+kL，其中 k 表示快指针在环上走的圈数。联立等式，可以得到
​ 2(a+b)=a+b+kL

解得 a=kL-b，整理可得

​ a=(k-1)L+(L-b)=(k-1)L+c

​ 从上述等式可知，如果慢指针从起点出发，快指针从相遇位置出发，每次两个指针都移动一步，则慢指针走了 a 步之后到达环的入口，快指针在环里走了 k-1 圈之后又走了 c 步，由于从相遇位置继续走 c 步即可回到环的入口，因此快指针也到达环的入口。两个指针在环的入口相遇，相遇点就是答案。

代码

解法一：哈希表判重

    public int findDuplicate(int[] nums) {
        Set<Integer> a=new HashSet<>();
        for(int i:nums){
            if(a.contains(i)){
                return i;
            }else{
                a.add(i);
            }
        }
        return 0;
    }

解法二：二分查找

 public static int findDuplicate(int[] nums) {
        int len = nums.length;
        int left = 1;
        int right = len - 1;
        while (left < right) {
            // 在 Java 里可以这么用，当 left + right 溢出的时候，无符号右移保证结果依然正确
            int mid = (left + right) >>> 1;

            int cnt = 0;
            for (int num : nums) {
                if (num <= mid) {
                    cnt += 1;
                }
            }

            // 根据抽屉原理，小于等于 4 的个数如果严格大于 4 个
            // 此时重复元素一定出现在 [1, 4] 区间里
            if (cnt > mid) {
                // 重复元素位于区间 [left, mid]
                right = mid;
            } else {
                // if 分析正确了以后，else 搜索的区间就是 if 的反面
                // [mid + 1, right]
                left = mid + 1;
            }
        }
        return left;
    }

解法三：快慢指针

public int findDuplicate(int[] nums) {
        int slow = 0, fast = 0;
        do {
            slow = nums[slow];
            fast = nums[nums[fast]];
        } while (slow != fast);
        slow = 0;
        while (slow != fast) {
            slow = nums[slow];
            fast = nums[fast];
        }
        return slow;
    }