机器人中的数值优化|【二】最速下降法，可行牛顿法的python实现，以Rosenbrock function为例
机器人中的数值优化|【二】最优化方法：最速下降法，可行牛顿法的python实现，以Rosenbrock function为例
在上一节中提到了我们详细探讨了数值优化/最优化理论中的基本概念和性质，现在开始使用python对算法进行实现。上一节链接：
机器人中的数值优化|【一】数值优化基础
导入依赖
导入依赖库并定义常量，C_CONSTANT为步长超参数，取0～1之间，停机准则STOP_CONSTANT，意为停止门限，当梯度的无穷范数低于这个门限时我们认为精度已经达到需求，停止进行计算
import numpy as np
import sympy as sp
from sympy import hessian
from sympy import oo
import numpy as np
from scipy.linalg import solve_triangular
import matplotlib.pyplot as plt
from types import MethodType
import time
# 步长超参数，取0～1之间
C_CONSTANT = 0.9
# 停止门限，当梯度的无穷范数低于这个门限时我们认为精度已经达到需求，停止进行计算
STOP_CONSTANT = 1e-6
定义基类
首先我们定义一个基本的优化方法类ZOptimization，在类中对法各种方法进行抽象的实现
class ZOptimization(object):
def __init__(self, dimensions) -> None:
self._optimizationName = 'z optimization'
self._version = '0.0.0.1'
self._dimensions = dimensions
self._core = None
def _getGradient(self, function, variables):
# sympy没有专门的求梯度函数，我们这里手动求偏导数再组装成向量
gradientList = []
for variable in variables:
gradient_i = sp.diff(function, variable)
gradientList.append(gradient_i)
return sp.Matrix(gradientList)
def _getHessian(self, function, variables):
# 直接调用自身hessian方法
return hessian(function, variables)
def _getProblemToSolve(self, dimensions):
return None, None
def _getDirectionFunction(self, gradient, hessian, variables, x_k):
return None
def _getConditionFunction(self, function, variables, direction, tau, x_k, gradient):
return None
def _update(self, x_k, tau, direction):
return [x_k[i] + tau * direction[i] for i in range(len(x_k))]
def search(self):
#初始化坐标点，这里默认坐标点在每个纬度上的值都为-2
x_k = [-2] * self._dimensions
iter = 0
functionToSolve, variables = self._getProblemToSolve(self._dimensions)
gradient_ = self._getGradient(functionToSolve, variables)
hessian_ = self._getHessian(functionToSolve, variables)
direction = self._getDirectionFunction(gradient_, hessian_, variables, x_k)
gradientVector = gradient_.subs([(variables[i], x_k[i]) for i in range(len(variables))])
gradientNorm = gradientVector.norm(oo)
# 记录一下迭代过程用于作图
x_k_list = []
z_list = []
while gradientNorm >= STOP_CONSTANT:
tau = self._getConditionFunction(functionToSolve, variables, direction, 1.0, x_k, gradient_)
x_k = self._update(x_k, tau, direction)
direction = self._getDirectionFunction(gradient_, hessian_, variables, x_k)
iter = iter + 1
gradientVector = gradient_.subs([(variables[i], x_k[i]) for i in range(len(variables))])
gradientNorm = gradientVector.norm(oo)
print("norm {}".format(gradientNorm))
print("Iter {}, x_k is {}, gradient is {}".format(iter, x_k, gradientNorm))
x_k_list.append(x_k)
z_list.append(functionToSolve.subs([(variables[i], x_k[i]) for i in range(len(variables))]))
return x_k, functionToSolve.subs([(variables[i], x_k[i]) for i in range(len(variables))]), x_k_list, z_list
这里我们设计了三个抽象方法_getDirectionFunction, _getConditionFunction, _getProblemToSolve，用于根据不同的情况下为我们的求解器类分别配置不同的优化方向计算模块，优化步长条件计算模块和自定义的问题模块（即我们自定义一个函数和函数的变量）。
_getGradient用于计算梯度，_getHessian用于计算Hessian矩阵，_update用于更新座标点。
线性搜索
在优化问题中，我们常用的架构无非是：
- 搜索下降方向
- 搜索确定下降步长
- 迭代确定新位置
在下降步长这里，最速下降法Steepest Gradient Descend和可行牛顿法Practical Newton’s Method我们都采用Armijo Condition作为判断，回顾机器人中的数值优化|【一】数值优化基础，我们有
Backtracking/Armijo line search
- 选择搜索方向： d = − ∇ f ( x k ) d=-\nabla f\left(x^k\right) d=−∇f(xk)
- 当 f ( x k + τ d ) > f ( x k ) + c ⋅ τ d T ∇ f ( x k ) f\left(x^k+\tau d\right)>f\left(x^k\right)+c \cdot \tau d^T \nabla f\left(x^k\right) f(xk+τd)>f(xk)+c⋅τdT∇f(xk)时，重复 τ ← τ / 2 \tau \leftarrow \tau/2 τ←τ/2
- 迭代 x k + 1 = x k + τ d x^{k+1}=x^k+\tau d xk+1=xk+τd
因此，直接进行代码实现
#不等式左侧计算
def ArmijoConditionLeft(function, variables, direction, tau, x_k):
return float(function.subs([(variables[i], x_k[i] + tau * direction[i]) for i in range(len(variables))]))
#不等式右侧计算
def ArmijoConditionRight(function, variables, direction, tau, x_k, gradient):
gd = gradient.subs([(variables[i], x_k[i]) for i in range(len(variables))])
dgd = direction.T * gd
return float(function.subs([(variables[i], x_k[i]) for i in range(len(variables))])) + \
float(C_CONSTANT * tau * dgd[0])
#不等式迭代
def ArmijoCondition(self, function, variables, direction, tau, x_k, gradient):
while ArmijoConditionLeft(function, variables, direction, tau, x_k) > \
ArmijoConditionRight(function, variables, direction, tau, x_k, gradient):
tau = tau / 2.0
return tau
搜索下降方向
最速下降法Steepest Gradient Descent Method
最速梯度下降的迭代形式如下所示
x k + 1 = x k − τ ∇ f ( x k ) x^{k+1}=x^k-\tau \nabla f\left(x^k\right) xk+1=xk−τ∇f(xk)
代码中则为
def lineSearchDirection(self, gradientVector, hessianMatrix, variables, x_k):
return -gradientVector.subs([(variables[i], x_k[i]) for i in range(len(variables))])
可行牛顿法Practical Newton’s Method
首先初始化 x x x, x ← x 0 ∈ R n x \leftarrow x_0 \in \mathbb{R}^n x←x0∈Rn
当 ∣ ∣ ∇ f ( x ) ∣ ∣ > δ ||\nabla f(x)|| > \delta ∣∣∇f(x)∣∣>δ时，进行如下计算
d o do do：
d ← − M − 1 ∇ f ( x ) d \leftarrow -M^{-1} \nabla f(x) d←−M−1∇f(x)
t ← b a c k t r a c k i o n g l i n e s e a r c h t \leftarrow backtrackiong \quad line \quad search t←backtrackionglinesearch
x ← x + t d x \leftarrow x + td x←x+td
e n d w h i l e end \quad while endwhile
r e t u r n return return
其中，M是一个接近Hessian阵的正定矩阵，以此来替代线性搜索中的求梯度和求Hessian阵。
如果函数为凸函数，则有
M = ∇ 2 f ( x ) + ϵ I , ϵ = min ( 1 , ∥ ∇ f ( x ) ∥ ∞ ) / 10 \boldsymbol{M}=\nabla^2 f(\boldsymbol{x})+\epsilon \boldsymbol{I}, \epsilon=\min \left(1,\|\nabla f(\boldsymbol{x})\|_{\infty}\right) / 10 M=∇2f(x)+ϵI,ϵ=min(1,∥∇f(x)∥∞)/10
因为M是正定的，因此可以使用Cholesky factorization
M d = − ∇ f ( x ) , M = L L T \boldsymbol{M} \boldsymbol{d}=-\nabla f(\boldsymbol{x}), \boldsymbol{M}=\boldsymbol{L} \boldsymbol{L}^{\mathrm{T}} Md=−∇f(x),M=LLT
如果函数是非凸的，那么我们通过如下计算M
Bunch-Kaufman Factorization:
M d = − ∇ f ( x ) , M = L B L T \boldsymbol{M} \boldsymbol{d}=-\nabla f(\boldsymbol{x}), \boldsymbol{M}=\boldsymbol{L} \boldsymbol{B} \boldsymbol{L}^{\mathrm{T}} Md=−∇f(x),M=LBLT
代码实现为
def practicalNewtonDirection(self, gradientVector, hessianMatrix, variables, x_k):
gradientVectorValue = gradientVector.subs([(variables[i], x_k[i]) for i in range(len(variables))])
epsilon = min(1, gradientVectorValue.norm(oo))/10.0
M = hessianMatrix.subs([(variables[i], x_k[i]) for i in range(len(variables))]) + epsilon * sp.eye(len(variables))
M = np.matrix(M.tolist()).astype(np.float64)
gradientVectorValue = np.matrix(gradientVectorValue.tolist()).astype(np.float64)
direction = cholesky_solve(M, -gradientVectorValue)
direction = sp.Matrix(direction.tolist())
return direction
# cholesky分解，使用cholesky分解是因为通过将正定矩阵进行LU分解
# 使用LU分解后的矩阵进行线性方程求解的速度比对原M矩阵求逆矩阵的速度要快很多
def cholesky_solve(A, b):
L = np.linalg.cholesky(A)
y = solve_triangular(L, b, lower=True, check_finite=False)
x = solve_triangular(L.T, y, lower=False, check_finite=False)
return x
注意可行牛顿法在这里使用了cholesky分解，使用cholesky分解是因为通过将正定矩阵进行LU分解，使用LU分解后的矩阵进行线性方程求解的速度比对原M矩阵求逆矩阵的速度要快很多，但是值得注意的是cholesky分解的时间复杂度仍然为 O ( N 3 ) O(N^3) O(N3)
问题定义
如图所示的一个2N维优化问题，我们可以把优化问题定义为如下所示
# 输入：维度 输出： 方程、变量列表
def initialProblem(self, dimensions):
functionToSolve = 0
variables = []
for i in range(dimensions):
variables.append(sp.Symbol('x'+str(i+1)))
for i in range(int(dimensions/2)):
functionToSolve = functionToSolve + 100 * ( variables[2*i] * variables[2*i] - variables[2*i+1] ) * \
( variables[2*i] * variables[2*i] - variables[2*i+1] ) + \
( variables[2*i] - 1 ) * ( variables[2*i] - 1 )
return functionToSolve, variables
使用代理模式，动态添加求解器类对象的方法
在这里由于求解器类中的几个方法都是抽象方法，所以需要体我们手动区实现。但是每个类我们根据需要去修改太麻烦了，能不能更根据我们的需要，在抽象的求解器基类“小车”上为我们动态添加我们需要的“工具”呢？这里我想到了Java的设计模式，代理模式（也有可能是其他名称，笔者混淆了）。通过定义好接口的基类，在抽象的基类上添加具体实现了方法的代理来完成各种复杂功能的组装。
但是，python中并没有接口这样的概念，因此我们换一种方法，通过动态添加方法来实现，具体如下所示。
if __name__ == '__main__':
#定义一个2维的Rosenbrock优化问题
zop = ZOptimization(2)
# 使用MethodType方法为类动态增加方法
zop._getProblemToSolve = MethodType(initialProblem, zop)
# zop._getDirectionFunction = MethodType(practicalNewtonDirection, zop)
zop._getDirectionFunction = MethodType(lineSearchDirection, zop)
zop._getConditionFunction = MethodType(ArmijoCondition, zop)
tick = time.time()
x_k, res, x_k_list, z_list = zop.search()
timeSpend = time.time() - tick
print("[optimization] Time cost is {} ns".format(timeSpend))
x_k_x = []
x_k_y = []
for i in range(len(x_k_list)):
x_k_x.append(x_k_list[i][0])
x_k_y.append(x_k_list[i][1])
fig, ax3d = plt.subplots(subplot_kw={"projection": "3d"})
ax3d.plot(x_k_x, x_k_y, z_list, 'ro-', label='Curve')
X = np.arange(-3, 3, 0.25)
Y = np.arange(-3, 3, 0.25)
X, Y = np.meshgrid(X, Y)
Z = 100 * (X * X - Y) * (X * X - Y) + (X - 1) * (X - 1)
ax3d.plot_surface(X, Y, Z, edgecolor='royalblue', lw=0.5, alpha=0.3, cmap='plasma')
ax3d.set_title('optimization of Rosenbrock function')
plt.show()
值得注意的是，为类动态增加方法时，我们的方法即使没有使用到self，也要在参数列表中添加这一项，否则就会报错，这一点很容易被忽略掉。比如：
# 输入：维度 输出： 方程、变量列表
def initialProblem(self, dimensions):
functionToSolve = 0
variables = []
for i in range(dimensions):
variables.append(sp.Symbol('x'+str(i+1)))
for i in range(int(dimensions/2)):
functionToSolve = functionToSolve + 100 * ( variables[2*i] * variables[2*i] - variables[2*i+1] ) * \
( variables[2*i] * variables[2*i] - variables[2*i+1] ) + \
( variables[2*i] - 1 ) * ( variables[2*i] - 1 )
return functionToSolve, variables
我们看到它虽然没有定义在类内，但是依然需要self参数。
实验结果
以2维Rosenbrock问题为例，当我们以[-2,-2]为优化的起点，停机条件为1e-6时，SGD用时80s左右，迭代2414轮；
NPM用时3s左右，迭代222轮。迭代过程如下所示
反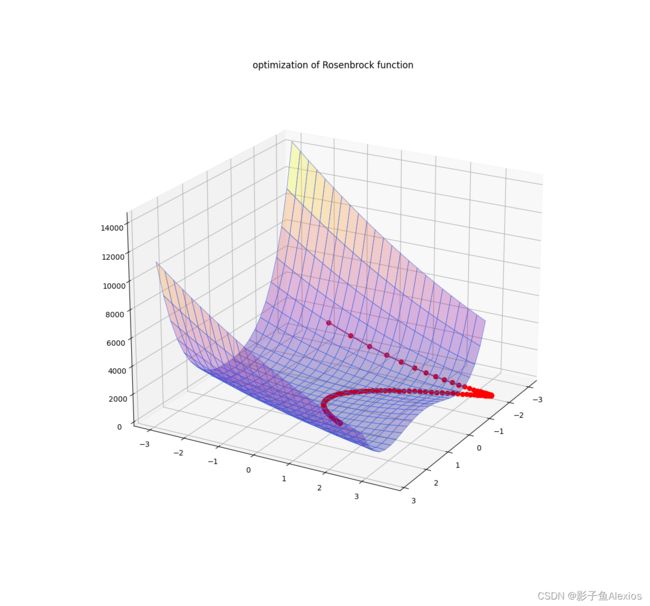
我们可以发现PNM的迭代步长相比于SGD更大，因此每一步效率更高。而SGD严格按照梯度下降。
PNM没有按照梯度下降的原因是PNM在迭代点处进行了二阶泰勒展开，这是一把双刃剑，虽然可以直接求出最优的迭代方向，但是又以后因为二阶展开产生了误差。
全部代码
'''
Description: optimization tutorials
version: 0.0.0.1
Author: Alexios Zhou
Date: 2023-01-09 10:41:48
LastEditors: Alexios Zhou
LastEditTime: 2023-01-10 15:26:40
'''
import numpy as np
import sympy as sp
from sympy import hessian
from sympy import oo
import numpy as np
from scipy.linalg import solve_triangular
import matplotlib.pyplot as plt
from types import MethodType
import time
C_CONSTANT = 0.9
STOP_CONSTANT = 1e-6
def initialProblem(self, dimensions):
functionToSolve = 0
variables = []
for i in range(dimensions):
variables.append(sp.Symbol('x'+str(i+1)))
for i in range(int(dimensions/2)):
functionToSolve = functionToSolve + 100 * ( variables[2*i] * variables[2*i] - variables[2*i+1] ) * \
( variables[2*i] * variables[2*i] - variables[2*i+1] ) + \
( variables[2*i] - 1 ) * ( variables[2*i] - 1 )
return functionToSolve, variables
def lineSearchDirection(self, gradientVector, hessianMatrix, variables, x_k):
return -gradientVector.subs([(variables[i], x_k[i]) for i in range(len(variables))])
def practicalNewtonDirection(self, gradientVector, hessianMatrix, variables, x_k):
gradientVectorValue = gradientVector.subs([(variables[i], x_k[i]) for i in range(len(variables))])
epsilon = min(1, gradientVectorValue.norm(oo))/10.0
M = hessianMatrix.subs([(variables[i], x_k[i]) for i in range(len(variables))]) + epsilon * sp.eye(len(variables))
M = np.matrix(M.tolist()).astype(np.float64)
gradientVectorValue = np.matrix(gradientVectorValue.tolist()).astype(np.float64)
direction = cholesky_solve(M, -gradientVectorValue)
direction = sp.Matrix(direction.tolist())
return direction
def cholesky_solve(A, b):
L = np.linalg.cholesky(A)
y = solve_triangular(L, b, lower=True, check_finite=False)
x = solve_triangular(L.T, y, lower=False, check_finite=False)
return x
def ArmijoConditionLeft(function, variables, direction, tau, x_k):
return float(function.subs([(variables[i], x_k[i] + tau * direction[i]) for i in range(len(variables))]))
def ArmijoConditionRight(function, variables, direction, tau, x_k, gradient):
gd = gradient.subs([(variables[i], x_k[i]) for i in range(len(variables))])
dgd = direction.T * gd
return float(function.subs([(variables[i], x_k[i]) for i in range(len(variables))])) + \
float(C_CONSTANT * tau * dgd[0])
def ArmijoCondition(self, function, variables, direction, tau, x_k, gradient):
while ArmijoConditionLeft(function, variables, direction, tau, x_k) > \
ArmijoConditionRight(function, variables, direction, tau, x_k, gradient):
tau = tau / 2.0
return tau
class Core(object):
def __init__(self) -> None:
self._coreNam = 'core'
class ZOptimization(object):
def __init__(self, dimensions) -> None:
self._optimizationName = 'z optimization'
self._version = '0.0.0.1'
self._dimensions = dimensions
self._core = None
def _getGradient(self, function, variables):
gradientList = []
for variable in variables:
gradient_i = sp.diff(function, variable)
gradientList.append(gradient_i)
return sp.Matrix(gradientList)
def _getHessian(self, function, variables):
return hessian(function, variables)
def _getProblemToSolve(self, dimensions):
return None, None
def _getDirectionFunction(self, gradient, hessian, variables, x_k):
return None
def _getConditionFunction(self, function, variables, direction, tau, x_k, gradient):
return None
def _update(self, x_k, tau, direction):
return [x_k[i] + tau * direction[i] for i in range(len(x_k))]
def search(self):
x_k = [-2] * self._dimensions
iter = 0
functionToSolve, variables = self._getProblemToSolve(self._dimensions)
gradient_ = self._getGradient(functionToSolve, variables)
hessian_ = self._getHessian(functionToSolve, variables)
direction = self._getDirectionFunction(gradient_, hessian_, variables, x_k)
gradientVector = gradient_.subs([(variables[i], x_k[i]) for i in range(len(variables))])
gradientNorm = gradientVector.norm(oo)
x_k_list = []
z_list = []
while gradientNorm >= STOP_CONSTANT:
tau = self._getConditionFunction(functionToSolve, variables, direction, 1.0, x_k, gradient_)
x_k = self._update(x_k, tau, direction)
direction = self._getDirectionFunction(gradient_, hessian_, variables, x_k)
iter = iter + 1
gradientVector = gradient_.subs([(variables[i], x_k[i]) for i in range(len(variables))])
gradientNorm = gradientVector.norm(oo)
print("norm {}".format(gradientNorm))
print("Iter {}, x_k is {}, gradient is {}".format(iter, x_k, gradientNorm))
x_k_list.append(x_k)
z_list.append(functionToSolve.subs([(variables[i], x_k[i]) for i in range(len(variables))]))
return x_k, functionToSolve.subs([(variables[i], x_k[i]) for i in range(len(variables))]), x_k_list, z_list
if __name__ == '__main__':
zop = ZOptimization(2)
zop._getProblemToSolve = MethodType(initialProblem, zop)
# zop._getDirectionFunction = MethodType(practicalNewtonDirection, zop)
zop._getDirectionFunction = MethodType(lineSearchDirection, zop)
zop._getConditionFunction = MethodType(ArmijoCondition, zop)
tick = time.time()
x_k, res, x_k_list, z_list = zop.search()
timeSpend = time.time() - tick
print("[optimization] Time cost is {} ns".format(timeSpend))
x_k_x = []
x_k_y = []
for i in range(len(x_k_list)):
x_k_x.append(x_k_list[i][0])
x_k_y.append(x_k_list[i][1])
fig, ax3d = plt.subplots(subplot_kw={"projection": "3d"})
ax3d.plot(x_k_x, x_k_y, z_list, 'ro-', label='Curve')
X = np.arange(-3, 3, 0.25)
Y = np.arange(-3, 3, 0.25)
X, Y = np.meshgrid(X, Y)
Z = 100 * (X * X - Y) * (X * X - Y) + (X - 1) * (X - 1)
ax3d.plot_surface(X, Y, Z, edgecolor='royalblue', lw=0.5, alpha=0.3, cmap='plasma')
ax3d.set_title('optimization of Rosenbrock function')
plt.show()