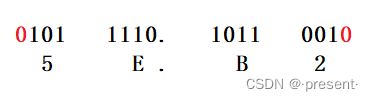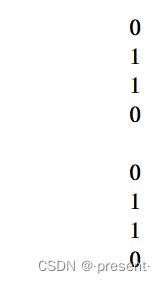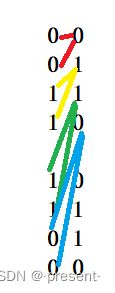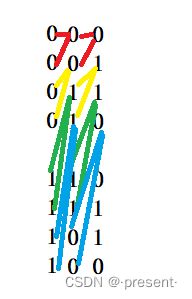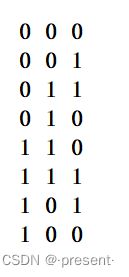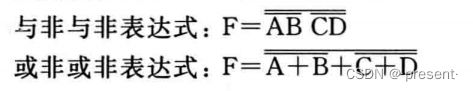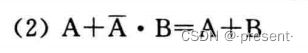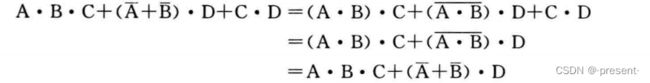逻辑代数的基本公式

目录

一.不同进制之间的转化

1.十进制和不同进制之间的转化方法

2.二进制和八进制的不同转化方法

3.二进制和十六进制的不同转化方法

4.十六进制和八进制的转化

二.二进制常用的编码形式

1.8421BCD码(恒权码)

2.格雷码 (循环码)

3.Ascll码 

三.逻辑代数的基本运算

1.与运算

2.或运算

3.非运算

4.其它常见逻辑运算

5.门电路

四.逻辑代数的基本公式与常用公式

1.常量公式

 2.变量公式

3.运算律

4.德摩根定律

5.还原律

6.常用公式

---

一.不同进制之间的转化

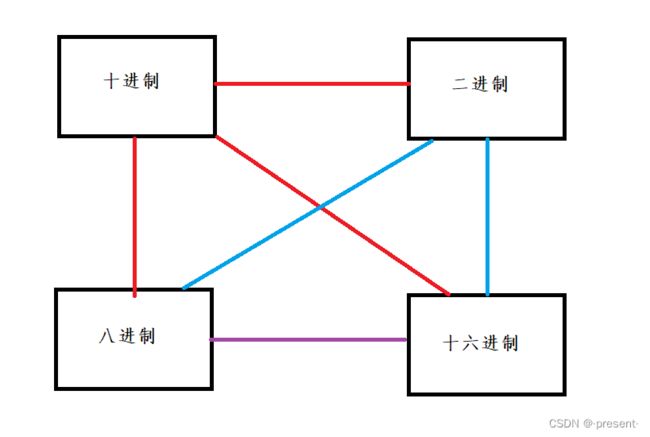
这个其实我们已经很熟悉了，我们接下来看一下这幅图，了解具体不同进制间是如何转化的.

1.十进制和不同进制之间的转化方法

首先，我们看红色这三条线，是十进制和不同进制之间的转化方法.

在这之前，我们必须先了解一个叫做位数和权的概念.

123.5这个十进制数，实际上可以分解为1 * 10^2 + 2 * 10^1 + 3 * 10^0 + 5 * 10^(-1)，而2,1,0,-1这些数就是位数，10^2就是1这个数的权,10^1就是2这个数的权...

也就是每位数虽然看上去都是0-9的取值,但它们的地位(权)可不同,或者说占的分量不同,1作为最高位对应的权重会更高.

比方说1101这个二进制数，转化为十进制数，也是如此，从右往左，位数依次增大

1 * 2^0 + 0 * 2 ^1 + 1 * 2^2 + 1 * 2^3 ，计算得到13,13便是1101这个二进制数转化为十进制数的结果.

再比如说2A.7F这个十六进制数，

2 * 16^1 + A(10)* 16^0 + 7* 16^(-1) + F(15) *16^(-2),计算得到42.49609375,便是2A.7F这个十六进制数转化为十进制数的结果.

至此，我们便可以类比，学会将所有进制数，转化为十进制数的方法.

总结：每一位数值乘以对应权重相加，即可任意数制转化为十进制.

那我们就要问，如何将十进制转为其它进制呢？
一般我们会将一个数分为两个部分进行处理，一个是整数部分，另一个则是小数部分，因为两个部分处理的方法是有差异的，前者是不断相除，从下往上取余数，后者则是不断相乘，从下往上取整数.

我们接下来举一个具体的例子,比如173.8125这个十进制数，我们想把它化为二进制数.

它的整数部分是173，小数部分是0.8125

对于整数部分173,我们就不断除以2，直到碰到被除数为1停止，然后从下往上取余数.

最后，173便化为10101101这样一个二进制数 .

对于小数部分0.8125，我们就不断乘2，直到乘到1为止，然后从上往下取整数排列.

PS:

1.值得注意，每次乘2后，所得的数，整数部分如果大于1,就要相应取出来，下次相乘就不再出现，比如下图第一次相乘得到的1.625，那第二次相乘是用0.625乘2，而不是1.625.

2.有时候一直得不到1，所以有部分十进制数未必能完全转化二进制数，只能不断逼近，这也导致计算机中C语言存储浮点数，未必精确，进而浮点数不能比较大小.

 最后，0.8125便化为1101这样一个二进制数

于是，把两者结合起来，便可以得到10101101.1101这样一个二进制数，这就是173.8125转化得到的二进制数.

实际上，为什么会有这种方法呢？我们可以仔细思索这个过程，它有点类似我们其它进制数得到十进制数的逆过程，173的每次相除，得到的余数，会随着相除次数增加，而对应位数增加，有种层层筛选的感觉，同理，0.8125也是如此.

总结：

整数部分，不断除2，从下往上取余数.

小数部分，不断乘2，从上往下取整数.

PS：十进制转十六进制，八进制，也是类似操作.

2.二进制和八进制的不同转化方法

接下来，我们看下蓝色的三条线间的关系.

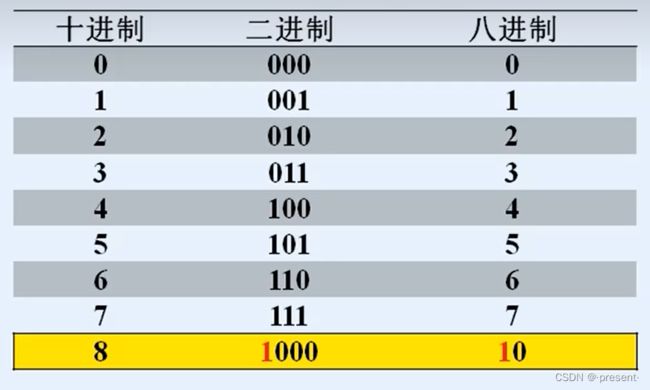
 对于11这个八进制数，对应十进制的9，二进制为1001，我们会惊奇地发现，三位二进制数恰好能够和八进制数一一对应，并且还会出现八进制进位，对应二进制也循环的现象，因此，我们就得到下面转化的方法.

从右往左，将3位二进制数看成一个整体，不足3位补0，等价为1个八进制数.

例如：1001看作001  001，刚好就对应八进制11，再比如1101，看作001 101，刚好也对应八进制15

反过来，把八进制转为二进制数，就是把每个数，对应化为二进制数即可.

比如52.43这个八进制数，先将每一位化为二进制数，然后再合起来，便得到101010.100011对应的二进制数了.

3.二进制和十六进制的不同转化方法

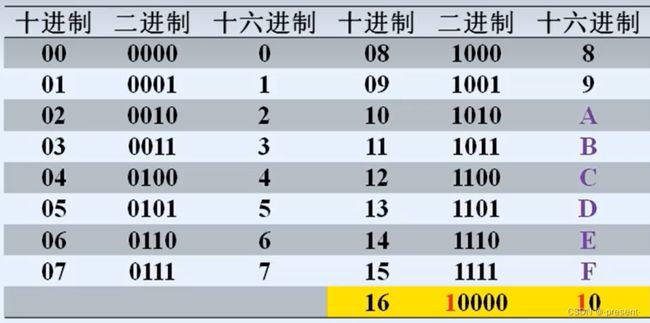
和八进制类似，4位二进制数也能够不重复和十六进制每个数一一对应，并且在十六进制进位时，二进制也恰好出现循环现象(10000中的0000) .

因此，我们可以得到如下转化方法

整数部分从右往左（小数部分从左往右）将4位二进制数看成一个整体，不足4位补0，等价为1个

十六进制数.

例如：

1011110.1011001这个二进制数，我们要把它转为十六进制数，将4位二进制数看成一个整体替换，不足就补0

十六进制转为二进制也类似八进制转为二进制，将每一位化成4位二进制即可，这里不再过多介绍.

4.十六进制和八进制的转化

没有特殊方法，将二进制作为桥梁，先转成二进制，再进一步转化为目标进制即可.

二.二进制常用的编码形式

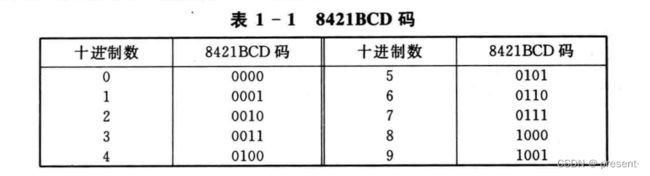
1.8421BCD码(恒权码)

BCD码即二-十进制代码，是用四位二进制数代码表示一位十进制数码.

它是一种有权码，也可被称为恒权码，从左往右的权值依次为8  4 2  1

类似还有2421码，5421码，顾名思义，就是权重分别为2  4  2  1和5  4  2  1的说法.

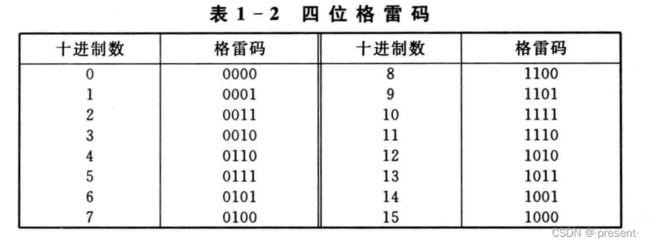
2.格雷码 (循环码)

格雷码一个特征就是，相邻两个码之间只有一位不同，每一位的状态都按一定顺序循环.

像上图列举的四位格雷码，每次变化，都只有1位二进制位变化，像0111和0101,就只有一个1发生变化，同样值得注意，1000和0000依旧也只有1位变化，是一个闭环的处理. 

格雷码的优势在于哪呢？

由于相邻代码只有一位发生变化，在代码过程转化过程中，不会出现过度“噪声”.

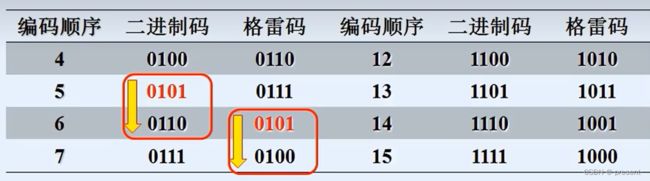
这是什么意思呢？举一个简单的例子,假设现在5要往6发生转变.

按照原来二进制码进行转化的话，理想情况，我们当然希望不同的两位会同时发生变化，但我们知道会有延迟，所以会导致出现两种情况

我可以先把0101，变成0111，再变成0110 ;

也可以先把0101，变成0100，再变成0110

而0111和0100是我们不希望要的信号，这就是过渡过程中的"噪声".

但格雷码就不会出现这种情况，每次都是直接一步完成.

那我们要怎么编写格雷码呢？

这里实际上是有规律的，我们先要把一组数0 1 1 0记在心中，最低位，一定是不断循环这四个数的

随后，每一个下一位新的数，都是上一个新的位上的数，循环出现两次.

这里我们写一个三位格雷码来加深理解这个过程.

首先，3位格雷码，2*2*2=8,必定有8个格雷码,我们先把最低位写出来.

那对于第二位，就是第一位的数，重复两次出现.0重复出现2次，接着是1出现2次，再接着是1出现2次，紧接着是0出现2次，刚好是8位，便不再循环.

 对于第三位，也是类似的操作.第二位的0重复出现2次，接着是0出现2次，再接着是0出现2次，紧接着还是0出现2次，刚好8位，不再循环. 

于是我们便得到3位的格雷码，如图所示，检查可以发现，完全符合格雷码的特点要求

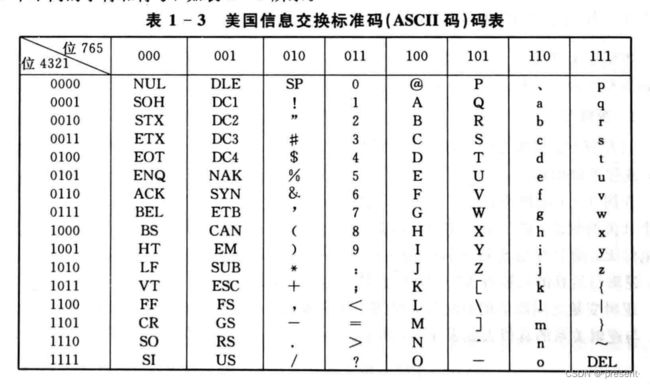
3.Ascll码 

即美国信息标准交换码，由一组7位二进制代码组成，共128个.

它是一种国际通用标准代码，广泛应用于计算机和通信领域.

这里也不再过多解释，每个符号对应相应的二进制码，需要的时候，直接查表就可以.

三.逻辑代数的基本运算

数码可以表示不同事物的不同状态，比方说汽车向前开，我们可以用1来表示，向后开，可以用0来表示；再比如红灯亮 ，我们用01表示，黄灯亮，用10表示，绿灯亮，用11表示，全部灯灭了，用00表示等等.

在这中，只有两种不同取值的变量，称为逻辑变量.

比方说，我们可以规定小于5V为低电压，用0表示，大于等于5V，用1表示，除了1，就是0，只有两种取值，这就是一个逻辑变量.

而研究逻辑变量之间的逻辑状态(关系)的推理运算，称为逻辑运算;

研究逻辑运算的数学方法,被称为逻辑代数.

基本运算分为三类：

我们用1表示开关接通，小灯泡发光；0表示开关断开，小灯泡熄灭.

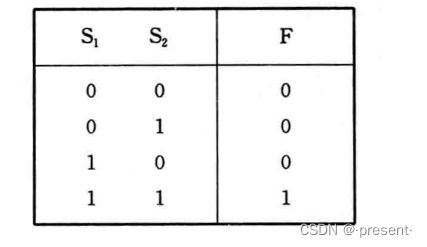
1.与运算

只有S1,S2同时接通，即都为1，才为1（小灯泡发光），其余都为0.

表示为F = S1 * S2 = S1S2.

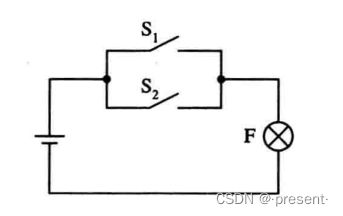
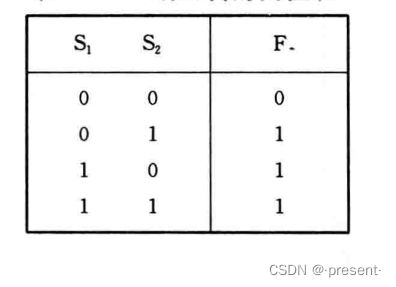
2.或运算

 

只要S1,S2有一个接通，即有一个为1，就为1（小灯泡发光）

只有S1,S2全部没有接通(都为0）,才为0（小灯泡熄灭）

表示为F = S1 + S2.

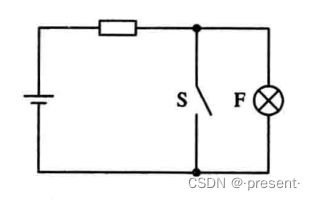
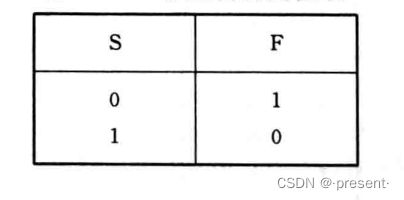
3.非运算

 

开关闭合(1)，灯泡必灭(0),反之，开关断开(0),灯泡发光(1).

表示为F = 

4.其它常见逻辑运算

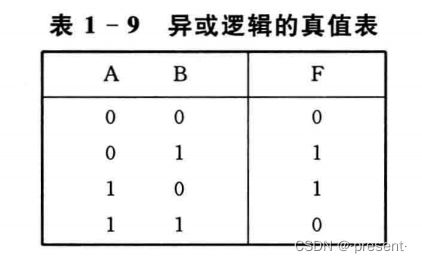
 异或运算     相同为0，相异为1   

1.两个相同的信号异或，得0   

2.与0做异或运算得原变量，与1做异或运算得反

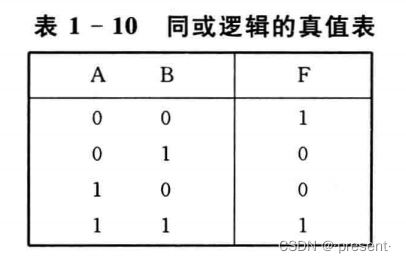
同或运算(异或运算的非运算)    相同为1，相异为0

与非运算（先与后非）F =    只有全为1，才为0，其余全为1

 或非运算（先或后非）F =     只要有1，必为0，只有全为0，才为1.

还有比如与非与非，和或非或非，这里不细谈

 

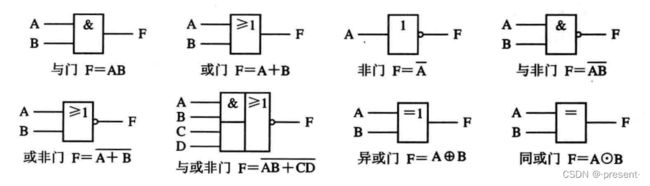
5.门电路

 当然，现在更多用得是下面这种形式

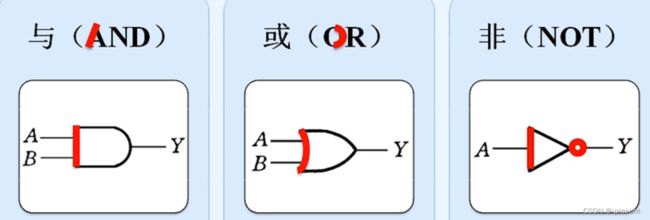
记忆方式也如上图所示，AND中的A是竖，因此图片左端为一竖线，OR中的O是弯，因此图片左端为一曲线，非则和上图类似，也是图片右端有个小圆圈. 

四.逻辑代数的基本公式与常用公式

为了加深对公式的理解，我们用数学中的集合概念进行类比记忆.

1就代表全集，0就代表空集，逻辑与对应交集，逻辑或对应并集，逻辑非对应取补集

1.常量公式

 2.变量公式

这里举A = 0来说明

A只能取0或者1，无论A取什么值，A和 必然不相等,而逻辑与只有全为1，才为1，所以得到的必为0.

从集合角度也很好理解，A和A的补集，两者的交集，必定为空集.

其它公式也可以类似理解，这里不一一说明.

3.运算律

 逻辑运算同样满足交换律(9，9‘)，结合律(10，10’)，分配律(11)

这里只解释不同于代数运算的特殊式子(11')

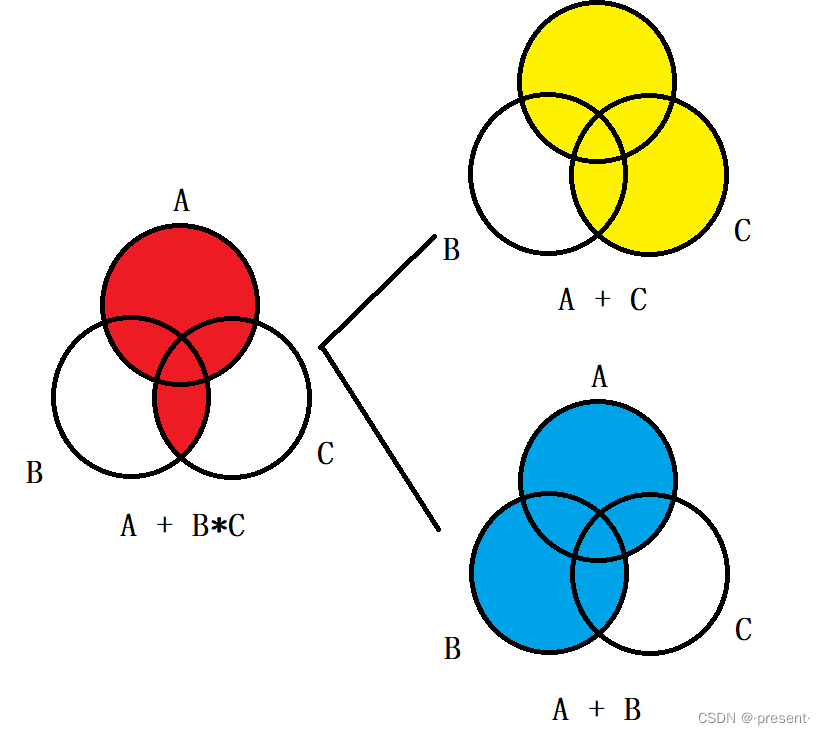
A + BC部分如左图所示，BC的交集与A的并集

A + C与A+ B两个集合想要得到左图，需要进行交集运算，对应逻辑与. 

证明： (A + B)(A + C) = A*A + B*A + A*C + B*C = A*(1 + B + C) + B*C= A + BC

4.德摩根定律

5.还原律

 很容易理解，两次非运算后，得到的依旧是其本身.集合补集的补集依旧是该集合.

6.常用公式

(1)集合与子集合并公式（加大乘小）

A + AB = A  (吸收律)

集合理解非常简单，加意味着取并集，那最终结果肯定为大的集合；乘意味着取并集，那最终结果

一定是小的集合.

含义：一个与项是另一个与项的因子，则另一个与项可以被吸收掉（也就是消失).

Lg.(A + B) + (A + B)*C*D = A + B

A * (A + B) = A

(2)消因子公式

证明： A + B = (A +) (A + B) = A + B

含义：在一个与或表达式中，如果一个与项的反是另一个与项的一个因子，则这个因子可以不要.

lg.

(3)消项公式

 证明： AB + C + BC(A + ) = (AB + BCA) + (C + BC) = (AB + ABC) + (C + CB) 

   = AB + C

PS:即便含BC组合而成的子项，也依旧可以消去.   AB + C + BCD = AB + C

lg.