图解LeetCode11：盛最多水的容器(多种解法)

LeetCode11：盛最多水的容器

给你n个非负整数a1，a2，… … ，an，每个数代表坐标中的一个点(i, a)。在坐标内画n条垂直线，垂直线i的两个端点分别为(i, ai)和(i, 0)。找出其中的两条先，使得它们与x轴共同构成的容器可以容纳最多的水。

说明：你不能倾斜容器

示例：

输入：[1,8,6,2,5,4,8,3,7]
输出：49

输入：[1,1]
输出：1

提示：

• n == height.length
• 2 <= n <= 10^5
• 0 <= height[i] <= 10^4

思路：

首先看到这道题有点迷糊，到达再说什么？？？

其实可以理解成一个数组和角标构成的柱状图，然后柱子就是杯壁，往里盛水

我们可以分步做解，如果一个数组[1, ,2, 1, 2]来说，我们以第一个数组作为边界，计算出其能容纳的最多的水，然后以第二个为边界，计算出其能容纳的最多的水，知道遍历数组，取出最大值

因为注水的过程中，只看最短的拿一个，也就是最短的杯壁

解法1：

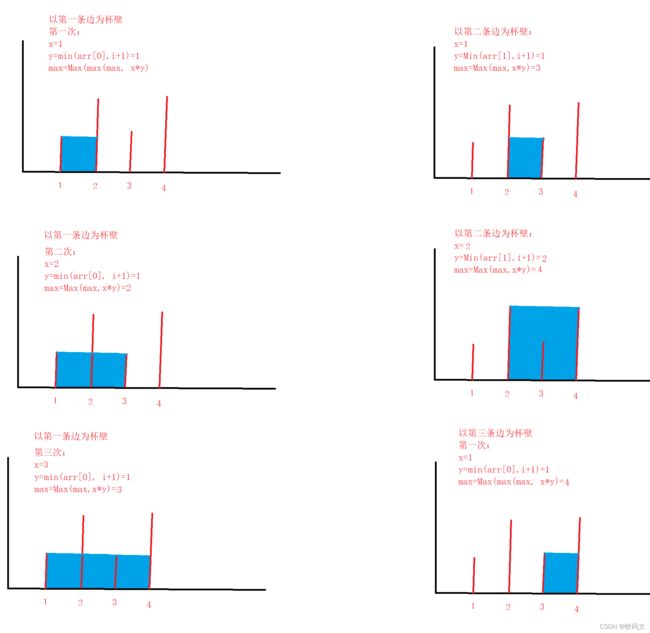
1. 以第一个数值为边界

   然后每次循环都将索引数值与杯壁比较，取小的那一个，然后更新容纳水的数值

   ①、第一次索引0的数值为1，此次遍历的位置为1数值是2，y=min(arr[0], 2)，y=1，max=Max（max，x*y)=1 * 1,所以第一次容纳水的大小为1
   

   ②、第二次索引0的数值为1，此次遍历的位置为2数值是1，y=min(arr[0], 1)，y=1，max=Max（max，x*y)=2 * 1,所以第一次容纳水的大小为2
   

   ③、第三次索引0的数值为1，此次遍历的位置为3数值是2，y=min(arr[0], 1)，y=1，max=Max（max，x*y)=3 * 1,所以第一次容纳水的大小为3
   

   ④、所以以第一个为数组，最多容纳水的数量为3

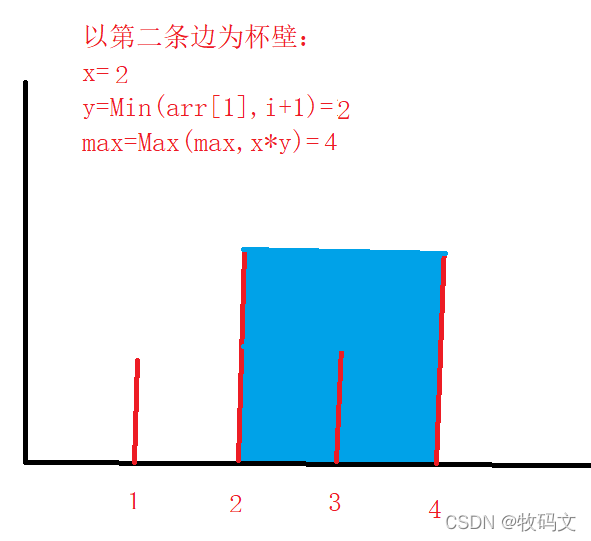
2. 将指针后移，以第二个边为杯壁

   ①、第一次索引1的数值为2，此次遍历的位置为2数值是1，y=min(arr[0], 1)，y=1，max=Max（max，x*y)=1 * 1,所以第一次容纳水的大小为1
   

   ②、第一次索引1的数值为2，此次遍历的位置为3数值是2，y=min(arr[0], 2)，y=2，max=Max（max，x*y)=2 * 2,所以第一次容纳水的大小为4

   

   ③、所以以第二条边为杯壁，最多容纳的水是4

3. 以第三条边为杯壁

   

4. 全部遍历结束，最后的结果是：容纳的最多的水是4

5. 全部的图解

   

代码实现：

public int getMaxWater(int[] ints){
    // 定义容纳最多的水
    int max = 0;
    // 获取数组长度
    int len = ints.length;

    // 遍历整数数组
    for (int i = 0; i < len - 1; i++) {
        // 定义y坐标
        int y = 0;
        for (int j = i+1; j < len; j++){
            // 比较数值和杯壁的大小
            y = Math.min(ints[i], ints[j]);
            // 更新max
            max = Math.max(max, y*(j-i));
        }
    }

    // 返回max
    return max;
}

解法2：

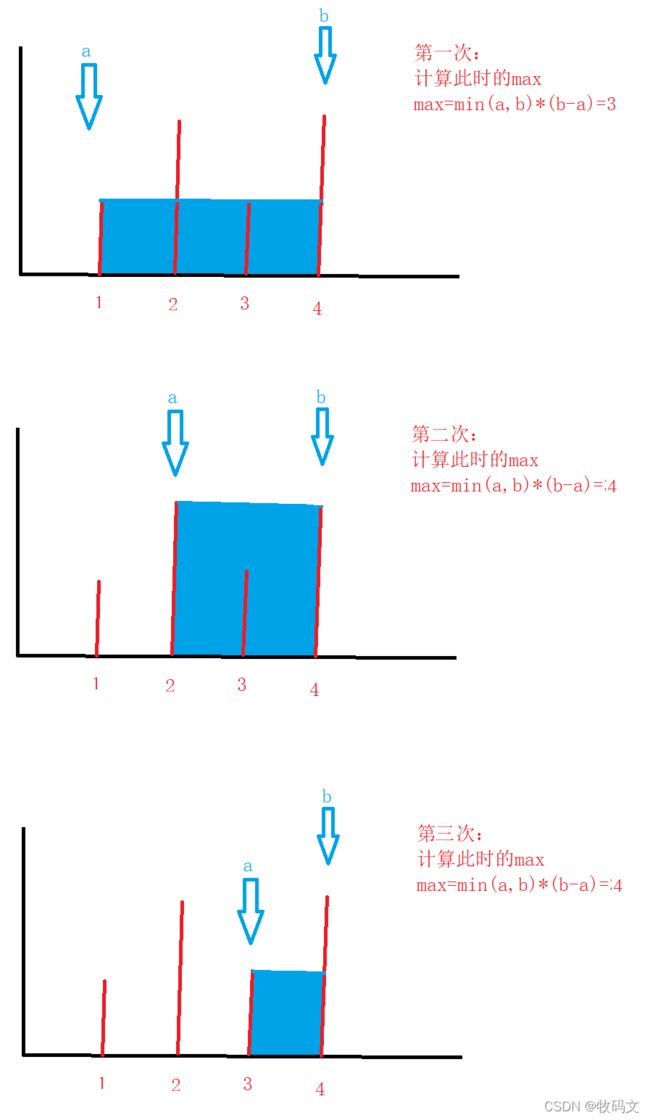
以上这种解法虽然可以取得最终的结果，但是造成了许多重复的计算，比如在第一次遍历的时候，就已经遍历了所有的数值，在中间有许多计算是很不必要的，所以我们可以采用双指针的解法，维护两个指针，分别从后向前，从前向后进行遍历，每次移动长度较小的那个指针，直到两个指针碰撞

由于容器的水是由杯壁的那个短的进行决定的，所以我们移动数值较大的指针，那么前者（两个指针指向的两个数值中的较小值）不会增加，而后者（指针之间的距离）会减少，所以这个乘积就会减小。因此我们要移动数字较小的指针

代码实现

public int getMaxWater2(int[] ints){
        // 定义最大容水量
        int max = 0;
        // 数组长度
        int len = ints.length;
        // 维护两个指针
        int i = 0, j = len - 1;
        while(i < j){
            // 指针索引数值小的那一个
            int minLen = Math.min(ints[i], ints[j]);
            max = Math.max(max, minLen*(j - i));
            if (ints[i] < ints[j]) i++ ; else j --;
        }
        return max;
    }

测试

public static void main(String[] args) {
        LeetCode11 lc = new LeetCode11();
        System.out.println(lc.getMaxWater(new int[]{3, 1, 2, 1, 2, 3}));
        System.out.println(lc.getMaxWater2(new int[]{3, 1, 2, 1, 2, 3}));
    }

结果：

15
15