数据结构-线段树(懒标记)乘除法混合
这里写目录标题
-
- 概念
- 为什么要用线段树来处理?
- 线段树实现
- 求最小值例题
- 懒标记(对区间修改)
- 模板题
- 运用懒标记维护最小值
- 运用线段树维护区间和且做乘法更新
- 乘除法混合
概念
线段树是擅长处理区间的,是一颗完美二叉树(所有的叶子节点的深度都相同,并且每个节点要么是叶子要么有两个儿子的的树),树上每一个节点维护一个区间,根维护整个区间,每个节点维护的是父亲的区间二等分后的一个子区间,当有n个元素时,对区间的操作可以在O(longn )的时间完成
结合图理解:
注意下图:绿色表示该节点维护的区间,红色表示该节点区间和,黑色表示该节点的编号
题:给定 一个数列[3,0,4,10]
问题一:查询区间[1,3]中元素的和
问题二:将a[2]的值改为99

为什么要用线段树来处理?
方法一:常规处理,对于问题的复杂度是O(n),问题二的复杂度是O(1)
方法二:利用前缀和,开一个数组来储存每个元素和前面所有元素的和,对于问题一复杂度就降到了O(1)(用b[3]-b[0]),问题二的复杂度从而上升到了O(n)(因为修改值后同时也要讲前缀和数组修改一遍)
所以上面两个方法数据量大了都会超时,特别当操作多了的时候,这个时候就可以用到线段树了,因为线段树无论是问题一还是问题二复杂度只有O(long n),相当于对所有操作均摊了复杂度
线段树实现
一、建树
利用父节点和左右儿子节点编号的关系,就可以用一维数组维护一颗二叉树
void build_tree(int node,int L,int R){//根节点,左端点,右端点
if(L==R){//当左右端点相等时,说明访问到了叶子结点
tree[node]=arr[L];//更新叶子节点的值
return;
}
int mid=(L+R)/2;//取区间中点
int left_tree=node*2;//取左儿子
int right_tree=node*2+1;//取右儿子
build_tree(left_tree,L,mid);//递归左树
build_tree(right_tree,mid+1,R); //递归右树
tree[node]=tree[left_tree]+tree[right_tree];//更新根节点的值
}
二、查询
如问题一查询区(1,3)的区间和,可以先分解为(1,2)(返回第二个节点的值 )和(3)(接着向下搜索,直到搜索到第六个节点返回),然后将两边的查询结果相加
int find_tree(int node,int L,int R,int x,int y){//查询x区间到y区间的和
if(x<=L&&R<=y){//此时节点保存的区间是需要的区间的子区间
return tree[node];//直接返回这个节点区间的值
}
int mid=(L+R)/2;
int left_tree=node*2;
int right_tree=node*2+1;
if(y<=mid){//要的区间完全在左子树
return find_tree(left_tree,L,mid,x,y);//要的区间保持不动,直接搜索左子树
}
if(x>=mid+1){//要的区间在右子树
return find_tree(right_tree,mid+1,R,x,y);//要的区间保持不动,直接搜索右子树
}
return (find_tree(left_tree,L,mid,x,mid)+find_tree(right_tree,mid+1,R,mid+1,y));//要的区间需要分叉,搜索左子树和右子树,并且将要的区间进行分叉搜索
}
三、更新
首先搜索该点的叶子节点,然后修改他的值,同时也要更新父节点的值,一直更新到根节点
void update_tree(int node,int L,int R,int x,int num){//将x点的值更新为num
if(L==R){//找到了x下标对应的叶子节点
tree[node]=num;//将叶子结点的值更新
arr[x]=num;//将数组的值同步更新
return;
}
int mid=(L+R)/2;
int left_tree=node*2;
int right_tree=node*2+1;
if(x<=mid){//在左子树
update_tree(left_tree,L,mid,x,num);//向左子树搜索
}else{//在右子树
update_tree(right_tree,mid+1,R,x,num);//向右子树搜索
}
tree[node]=tree[left_tree]+tree[right_tree];//父节点也要更新
}
测试完整代码:
#include求最小值例题
给定数列[5,3,7,9,6,4,1,2],用线段树进行下面操作
1.查询区间[4,8]的最小值
2.将下标为7的值改为100
#include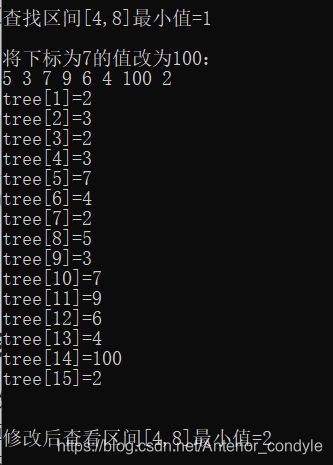
对于线段树tree[]数组需要维护的数据的意义,视具体情况而定,在对应的地方做出相应改变即可
懒标记(对区间修改)
对于上述处理,一旦遇到对一段区间进行更新,如果每次要搜到根节点再更新的话的话,可想而知复杂度会很高,所以就引入了懒标记进行优化
懒标记的作用:对每个节点打一个改变标记,代表他的子孙所有节点都进行了这个变化,但是懒就懒在确定标记之后就不再去更新子孙节点了

懒标记我习惯使用结构体进行保存,即对树的每个节点定义两个属性
struct node{
long long sum,lazy;//sum表示区间和,lazy代表懒标记
};
node tree[100000005];//定义树数组
假如现在要对区间[1,3]的每个元素执行加num操作,只需要搜索到tree[2]和tree[3]([1,3]的区间)然后将这个两个节点的lazy属性进行标记,表示这个节点和他的子孙都执行了这个操作(加num操作)
标记代码段:
if(x<=L&&R<=y){//找到了需要查找区间的子区间段
tree[node].lazy+=num;//标记变化值
tree[node].sum+=(R-L+1)*num;
//(R-L+1)*num 表示这个区间变化的值(元素个数*num,因为他的孙子叶子节点每个都要+num)
return;
}
到了这里有一个疑问,加入我们进行了下一个操作,将arr[2]的值加了100,那我们上一步的增加的值不就无效了吗?
这里又用到了一个小技巧,将标记下推,也就是将刚才tree[2]的标记推给他的两个孩子tree[2]和tree[1],这样就不担心丢失上一步的变化值了
下推代码段:
void PushDown(int node,int len){
if(tree[node].lazy!=0){//当前节点被标记过,就推给他的儿子节点
tree[node<<1].lazy+=tree[node].lazy;//lazy传下去
tree[node<<1|1].lazy+=tree[node].lazy;
tree[node<<1].sum+=(len-(len>>1))*tree[node].lazy;//儿子的区间和也计算出来,
tree[node<<1|1].sum+=(len>>1)*tree[node].lazy;
tree[node].lazy=0;//必须将标记去除,要不然会重复再一次传给他的孩子
}
}
下推在更新时需要使用,因为会存在更新标记过的区间的子区间,
查询时也必须使用,会存在查询的区间是标记过的区间的子区间
参考代码:
#include模板题
#include运用懒标记维护最小值
#include运用线段树维护区间和且做乘法更新
#include乘除法混合
对于乘除法混合,记住关键点“乘法优先,在做加法”
下推:
1.下推区间和时,必须先做乘法再做加法
2.下推乘法标记,直接下推
3.下推加法标记,本身加法标记*本身乘法标记+父亲加法标记
4.必须清空标记
void push_down(int node,int len){
int leftlen=len-(len>>1);//做孩子区间大小
int rightlen=len>>1;//右孩子区间的大小
//下推和(注意:先乘法在加法)
tree[left].sum=tree[left].sum*tree[node].muti+tree[node].add*leftlen;
tree[left].sum%=p;
tree[right].sum=tree[right].sum*tree[node].muti+tree[node].add*rightlen;
tree[right].sum%=p;
//下推乘标记
tree[left].muti=(tree[left].muti*tree[node].muti)%p;
tree[right].muti=(tree[right].muti*tree[node].muti)%p;
//下推加标记(标记也要先乘后加)
tree[left].add= (tree[left].add*tree[node].muti+tree[node].add)%p;
tree[right].add = (tree[right].add*tree[node].muti+tree[node].add)%p;
//清空标记
tree[node].add=0;
tree[node].muti=1;
}
乘法更新:
1.区间和正常乘
2.乘法标记正常乘
3.一定要同时将加法标记也同时更新(乘于这个倍数)
if(x<=L&&R<=y){//[L,R]区间需要更新
tree[node].sum=(tree[node].sum*k)%p;//更新和
tree[node].muti=(tree[node].muti*k)%p;//更新乘法标记
tree[node].add=(tree[node].add*k)%p;//一旦执行乘法,加法标记也需要乘一遍(先乘后加原则)
return;
}
加法更新:
正常加就可以了,因为即使做过乘法在执行乘法是就已经处理过加法标记了
if(x<=L&&R<=y){
tree[node].sum=(tree[node].sum+(R-L+1)*num)%p;//直接加就可以了,因为如果执行过乘法,已经提前处理过
tree[node].add=(tree[node].add+num)%p;//加法标记一样
return;
}
完整代码:
#include版本二:
#include
