小白回顾------线段树讲解

课前啰嗦：
算法这东西，也不是一时半会能理解的，灵活运用更难，所以今天我做一个线段树讲解，用于自身的理解.
Part I:
先了解线段树：
线段树是一种二叉树，也就是对于一个线段，我们会用一个二叉树表示。比如说一个长度为4的线段，我们可以表示成

1--->4的线段可以分成1---->1 2---->2 3---->3 4---->4
线段树：
目前可以看出来，一个大区间会分成很多小区间，这些区间一直再分，直到l==r时不再分
这样线段树的功能我想也能猜到一部分可以对所有的区间附上权值
举个栗子：
假如我们要求1--->4区间内任意一段区间的和
惯性思维：用暴力循环求解,但这样在数据量小的时候，还行，但对于数据量太大的情况下，肯定会T，并且询问次数很少的情况下，如果数据量很大，并且询问次数很多，每次都询问1---1e8的和，那不是每次都需要循环1---1e8次
暴力代码附上：

    int sum=0;
    for(int i=l; i<=r; i++)//l,r代表区间的上下限
    {
        sum+=a[i];//a[i]代表区间内每个点的权值
    }

此时线段树的作用就有了，我们可以将一个大区间分为很多小区间，然后回溯，大区间的权值和便可以get到了
列如上例：
1--2的权值和可以为1--1+2--2，3--4.valsum=3--3.valsum+4--4.valsum
按照从下往上的顺序依次递推便可以得到所有区间的和
但有一个小Bug按照上例2--3.valsum,该如何求呢？
这里涉及了一个小技巧的操作之后讲明
线段树.build_tree(建树）：
首先我门要操作线段树，肯定要把树建好，不然没有根基
建树顺序从上到下，依次赋值
维护区间：

void update(int k)
{
    tree[k].sum=(tree[k*2].sum+tree[k*2+1].sum);
}

结点k的sum=k的左孩子sum+k的右孩子sum
建树代码：

void build_tree(int k, int l,int r)
{
    tree[k].l=l,tree[k].r=r;//记录树的左右子叶
    if(l==r)
    {
        tree[k].sum=a[l];
        return ;
    }
    int mid=(l+r)/2;
    build_tree(k*2,l,mid);
    build_tree(k*2+1,mid+1,r);

    update(k);
}

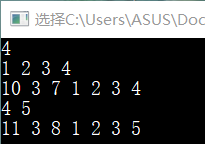
数据详解：

解释：
1:首先输入区间长度为1---4
2:第二行代表每个点的权值
3:第三行代表建树后每个结点的和
第三行图解：

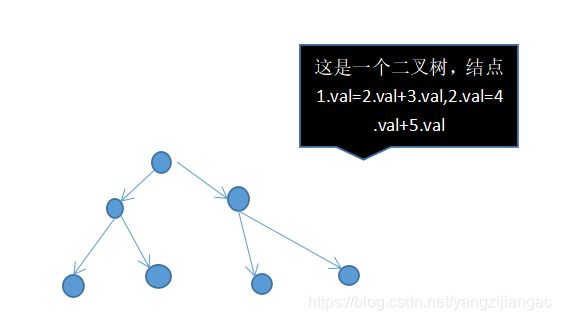
结合数据图：
1.val=10 2.val+3.val=10 这样看是否理解建树呢，理解二叉树的性质便可以理解建树
线段树.point_change(单点修改）:

假如我们要去修改结点7，依据数据解析可知，结点7.val=4，当我们更新了节点7时，我们要依次更新它的爸爸，爷爷，也就是结点3和结点1，这样就可以将区间的和更改，并不影响，后续操作

在第四行我修改了第二行的第四个点的权值，将其修改为5
之后依次修改了他的上方父辈，3结点，1结点
注解：
我想可能会有人觉得这样的操作很复杂，很繁琐，但是根据二叉树的结构，这样将复杂度降到了logn,真的很快
举个栗子：
二分查找1---100里的一些数，比如我们要查到50，二分分一次即可，for遍历需要50次，对于更大的数二分的效果更加明显
单点修改代码：

void point_change(int k,int x,int y)//单点修改
{
    if(tree[k].l==tree[k].r)
    {
        tree[k].sum=y;
        return ;
    }
    int mid=(tree[k].l+tree[k].r)/2;
    if(mid>=x)
        point_change(k*2,x,y);
    else
        point_change(k*2+1,x,y);
    update(k);
}

注：
mid代表的是二分后的结点，我们肯定要确定x，x的爸爸，x的爷爷，我们将mid与x比较，即可获得x的位置，当mid在k*2+1的时候，x在k*2,反之亦然
线段树.query_sum(区间求和）:
1：
可能有很多小伙伴们，和曾经的我一样，一直认为query_sum()的作用是求区间和，其实不是query_sum()的作用是询问区间的和，因为我们在建树的时候已经将区间的和给求出来了，线段树的作用得益于update(),update()维护区间的性质改变线段树的性质
2：
询问和其实很简单，这里我们对代码讲解一下便可以理解
代码：

int query_sum(int k,int l,int r)
{
    if(tree[k].l>=l&&tree[k].r<=r)
    {
        return tree[k].sum;
    }
    int mid=(tree[k].l+tree[k].r)/2;
    if(mid>=r)
        return query_sum(k*2,l,r);
    if(mid

讲解：
如果我们的询问的区间在有效的区间里时，直接返回answer即可，如果不在我们就要去寻找有效区间，当mid>=r时肯定要返回到有效区间里我们就操作return query_sum(k*2,l,r),当mid我们也要返回有效区间中return query_sum(k*2+1,l,r)当两种情况都不满足，就遇到了，最开始说的情况

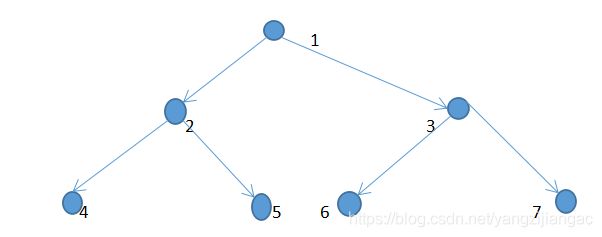
举个栗子我们要求5--6的和通过询问他们的父亲肯定不行了，所以就要操作 return query_sum(k*2+1,mid+1,r)+query_sum(k*2,l,mid)

总结：
线段树我接触到现在也有很长时间了，但在短时间内理解它，对我来说真的不是很容易，所以做到多多回顾，写写博客有助于理解，当理解之后写线段树基本就不用靠板子了，还是很好的，线段树的水还是很深的