数据结构---二叉树

目录

树的概念

相关概念

相关性质

二叉树

满二叉树

完全二叉树

二叉树的性质

二叉树的存储

链式存储

二叉树的遍历

 二叉树的基本操作

---

树的概念

树（Tree）是一种抽象数据类型（ADT）或是实现这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>0）个有限节点组成一个具有层次关系的集合

相关概念

结点的度：一个结点拥有子树的个数

如上图：A节点的度为3，B结点的度为2，C结点的度为0

树的度：树中所有结点的度中的最大值

如上图：树的度为3

叶子节点：度为0的结点

如上图：C D E F是叶子结点

深度：对于任意节点n,n的深度为从根到n的唯一路径长

如上图：A结点深度1，C结点深度2，F结点深度3

树的高度：根节点到叶子结点的路径长

如上图：树的高度：3

相关性质

对于任何一个树，有n个结点，那么有n-1条边

二叉树

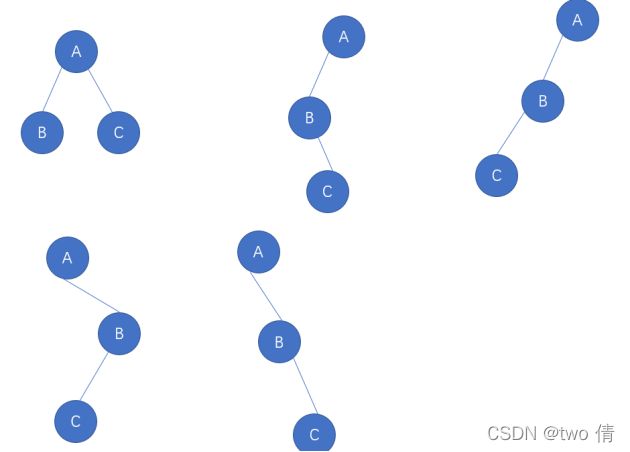
二叉树每个结点最多只有两个子树，且分为左子树和右子树，两个子树不可颠倒顺序

有三个结点的二叉树有5种

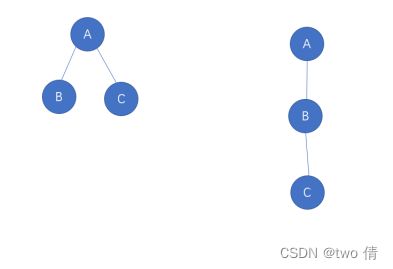
 有三个结点的普通树有2种

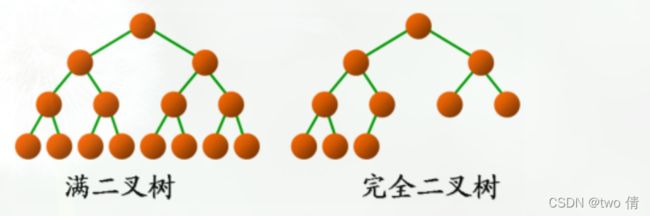
满二叉树

如果二叉树有n层，那么一共有2^（n -1）个结点的二叉树就是满二叉树

完全二叉树

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与中满二叉树编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉树。 

​

二叉树的性质

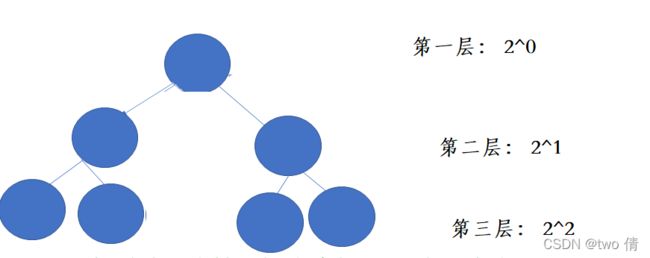
1、如果二叉树有n层，那么最多一共有2^（n -1）个结点

2.如果二叉树有n层，那么每一层最多有2^n -1个结点

​

 3、对于任何一个二叉树：度为0的结点个数=度为2的结点个数+1

​

 4、具有n个结点的完全二叉树的深度：log2 n + 1 

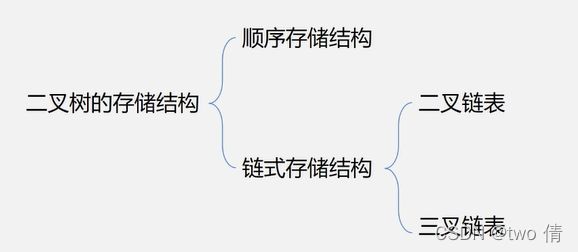
二叉树的存储

二叉树的存储形式：顺序存储和链式存储

链式存储

孩子表示法：

class BTNode {
    int val;
    BTNode left;//存储左孩子结点
    BTNode right;//存储右孩子结点
}

孩子双亲表示法：

class BTNode {
    int val;
    BTNode left;//存储左孩子结点
    BTNode right;//存储右孩子结点
    BTNode parent;//存储父亲结点
}

二叉树的遍历

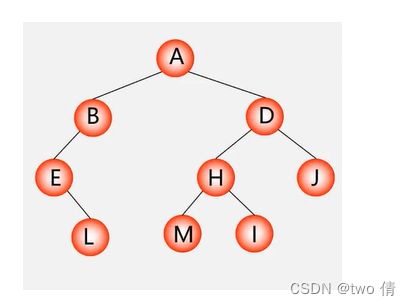
先序得到ABELDHMIJ 

中序得到 ELBAMHIDJ

后序得到 LEBMIHJDA

层次得到ABDEHJLMI

 先序：ABDGCEHF

中序：DGBAEHCF

后序：GDBHEFCA

知道了二叉树的先序和中序或者中序和后序可以唯一确定一个二叉树。

根据信息，画出二叉树

先序：A B C D E F G H I J

中序：C D B F E A I H G J

解析：根据特点：先序中知道A是根，在中序中知道C D B F E是A的左子树，I H G J是A的右子树

对于中序：C D B F E：先序中元素顺序：B C D E F那么B是根，C D是左子树，F E是右子树

对于中序C D：先序中元素顺序C D，那么C是根， D是右子树

对于中序F E：先序中元素顺序E F，那么E是根， F是左子树

对于中序I H G J：先序中元素顺序G H I J，那么G是根， I H是左子树，J是右子树

对于中序I H，先序中元素顺序H I ，那么H是根，I是左子树

中序：B D C E A F H G

后序：D E C B H G F A

后序中确定A是根，在中序中确定B D C E 是左子树，F H G是右子树

对于元素B D C E：中序中是B D C E,后序是D E C B那么B是根，D C E是右子树

对于元素D C E：中序中是D C E，后序是D E C 那么C是根，D是左子树，E是右子树

对于元素F H G：中序中是F H G，后序是H G F  那么F是根，H G是右子树

 对于元素H G：中序中是H G，后序是H G 那么G是根，H是左子树

 二叉树的基本操作

创建二叉树

  public static int i = 0;
    public static BTNode initTree( String str) {
         BTNode  root=null;
        if (str.charAt(i) == '#') {
            i++;
        } else {
             root = new BTNode(str.charAt(i));
            i++;
            root.left = initTree(str);
            root.right = initTree(str);
        }
        return root;//程序结束最终执行---返回了根节点
    }

前序遍历

 public static void prevOrder(BTNode node){
        if(node==null)
            return;
        System.out.print(node.val+" ");
        prevOrder(node.left);
        prevOrder(node.right);
    }

 中序遍历

 public static void inOrder(BTNode node){
        if(node==null)
            return;
        inOrder(node.left);
        System.out.print(node.val+" ");
        inOrder(node.right);
    }

后序遍历

public static void postrder(BTNode node){
        if(node==null)
            return;
        postrder(node.left);
        postrder(node.right);
        System.out.print(node.val+" ");
    }

 层次遍历

    public static void levelOrder(BTNode root) {
        if (root == null) return;
        Queue queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            BTNode node = queue.remove();
            System.out.print(node.val + " ");
            if (node.left != null)
                queue.offer(node.left);
            if (node.right != null)
                queue.offer(node.right);
        }
    }

 获取结点的总个数

count不能是成员变量，否则递归会重新初始化 

 static int count=0;
    public static int numCount(BTNode node){
        if(node==null)
            return 0;
        count++;
        numCount(node.left);
        numCount(node.right);
        return count;
    }

 总结点个数：左子树的结点个数+右子树的结点个数+1(根节点）

 public static int sz(BTNode node){
        if(node==null)
            return 0;
        return sz(node.left)+sz(node.right)+1;
    }

叶子节点的个数 

叶子节点个数=左子树叶子结点+ 右子树叶子结点

  public static int nodeSz(BTNode node){
        if(node==null)
            return 0;
        if(node.right==null&&node.left==null)
            return 1;
        return nodeSz(node.left)+nodeSz(node.right);
    }

树的深度

左右子树深度的最大值+1

 public static int deepTree(BTNode node){
        if(node==null)
            return 0;
        return deepTree(node.left)>deepTree(node.right)? deepTree(node.left)+1:deepTree(node.right)+1;
    }

 第k层结点的个数

 public static int countLevel(BTNode node,int k){
        if(node==null)
            return 0;
        if(k==1)
            return 1;
        return countLevel(node.left,k-1)+countLevel(node.right,k-1);
    }

上述代码得到了高度又去递归了，会超出时间限制

 public int maxDepth(TreeNode root) {
  if(root==null)
            return 0;
            int right=maxDepth(root.right);
            int left=maxDepth(root.left);
        return right>left? right+1:left+1;
    }

是否含有某个元素

    public static boolean contains(BTNode node,char val) {
         if (node == null)
            return false;
        if (node.val == val)
            return true;
      return contains(node.right, val)|| contains(node.left, val);
}

 是不是完全二叉树

    public static boolean isCompleteTree(BTNode node){
        if(node==null)return true;//空树也是完全二叉树
        Queuequeue=new LinkedList<>();
        queue.add(node);
      while(!queue.isEmpty()){
          BTNode s=queue.remove();
          if(s!=null){
              queue.add(s.left);
              queue.add(s.right);
          }else{
              break;
          }
      }
        while(!queue.isEmpty()) {
            BTNode s = queue.remove();
            if (s != null)
                return false;
        }
        return true;
    }