C++实现图 - 03 最小生成树
数据结构与算法专栏 —— C++实现
写在前面:
这一讲来讲一个图中非常重要的内容 —— 最小生成树,在此之前我们先来回顾一下生成树的概念。
生成树的定义
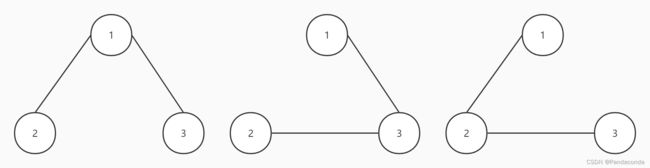
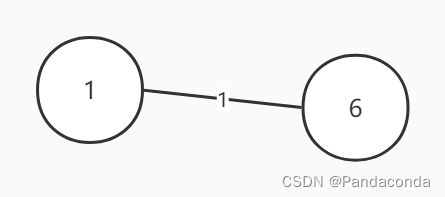
一个连通图的生成树是一个极小的连通子图,它包含图中全部的 n 个顶点,但只有构成一棵树的 n-1 条边。说人话就是我要用最少的边将所有结点连接起来,直接上图:
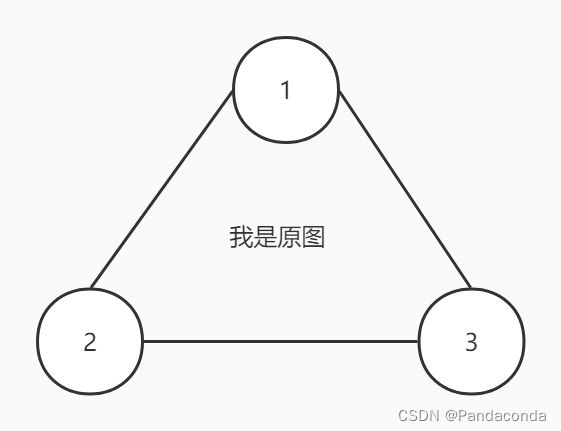
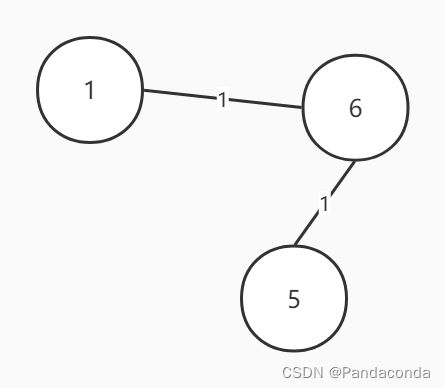
而这个原图的生成树就有一下三个:
由此可以知道对于包含 n 个顶点的无向完全图最多包含 n 的 n-2 次方颗生成树。
最小生成树
最小生成树是带权图当中所有边权之和最小的生成树,对于一个无权图它只有生成树而没有最小生成树。
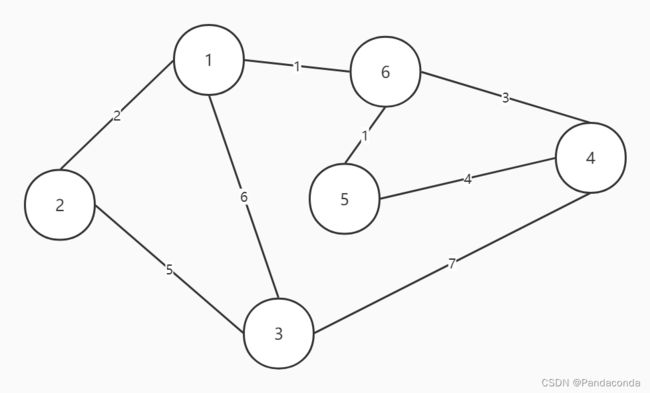
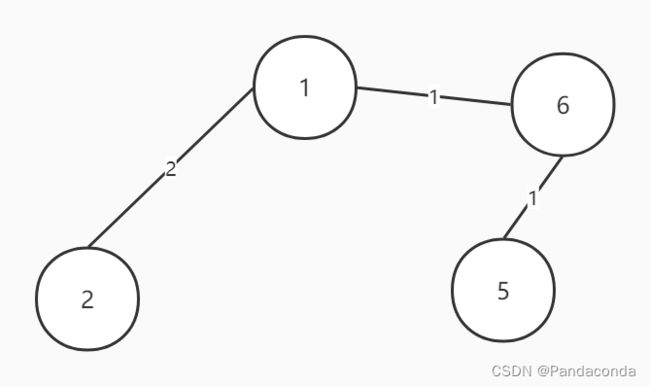
我们还是直接看图理解,假设有这样一个带权无向图:
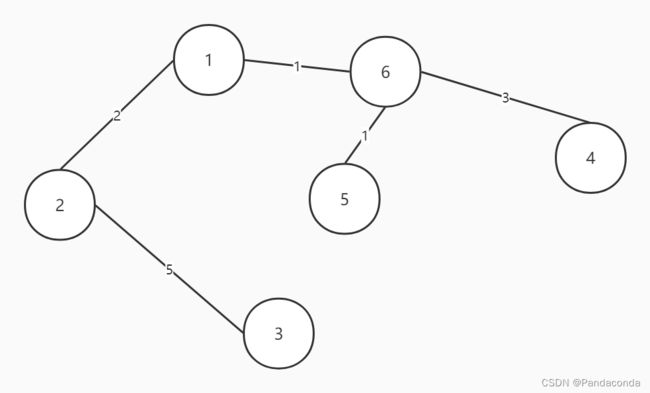
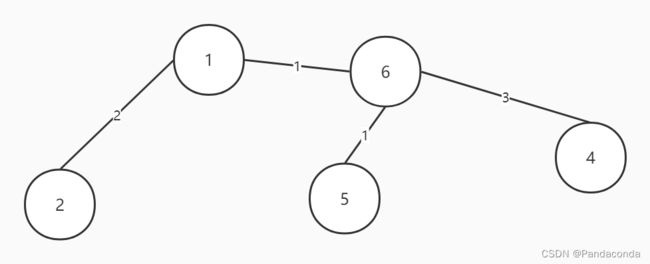
那么我们可以得到它的最小生成树:
通过计算可以知道,其所有边权之和为 2+1+1+4+5 = 23 ,是所有生成树中最小的一颗,其它生成树的边权之和都要比它的要大。
那么问题来了,我们知道最小生成树是什么了,那如何得到最小生成树呢?
最小生成树算法有很多,但是我们这里只讲最经典的两个,也是面试和笔试中常用的两个算法,克鲁斯卡尔(Kruskal)算法和普里姆(Prim)算法。
克鲁斯卡尔(Kruskal)算法
克鲁斯卡尔算法(Kruskal)是⼀种使用贪婪方法的最小生成树算法。它的实现思路是:
1、先将所有边放在一个数组当中,并且按照边权的大小进行从小到大的排序。
2、然后从数组中选一条权值最小的边,如果不能构成回路则加入树中。
3、重复上述操作,直到所有结点都加入到树中。
我们还是直接上图:
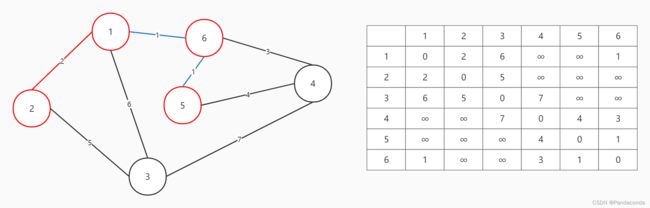
第一步:对所有边权进行从小到大排序,开始从头遍历每一条边。
第二步:选择边权最小的边 1 -> 6 ,发现不会成环,添加此边。
第三步:选择边 5 -> 6 ,发现不会成环,添加此边。
第四步:选择边 1 -> 2 ,发现不会成环,添加此边。
第五步:选择边 4 -> 6 ,发现不会成环,添加此边。
第五步:选择边 4 -> 5 ,发现会成环,舍弃此边。
第六步:选择边 2 -> 3 ,发现不会成环,添加此边。
此时所有结点都已经在生成树中,故结束遍历。
接下来我们来看该如何实现上述操作,这里就要用到我们之前学的并查集了,记不清楚的小伙伴可以回顾我之前的文章:
树 - 08 并查集
这里因为涉及到判断是否成环的问题,所以我们要通过并查集来查找每次新加入的边的两个结点是否已经有通路。
克鲁斯卡尔算法实现的核心其实就是并查集,除此之外其实没有什么特别复杂的地方,我们直接来看代码。
全部代码
#include普里姆(Prim)算法
普里姆算法在找最小生成树时,将顶点分为两类,一类是在查找的过程中已经包含在生成树中的顶点(假设为 A 类),剩下的为另一类(假设为 B 类)。
具体思路如下:
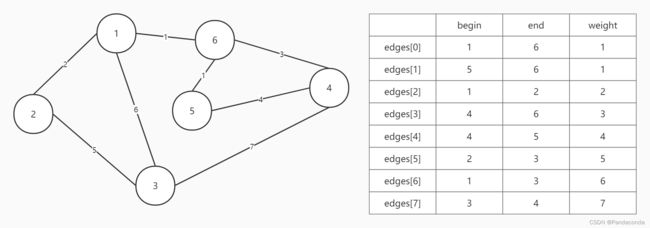
1、我们将所有边放在邻接矩阵中。
2、最开始先创建一个额外的集合,初始化放入一个结点。
3、每次从这个集合中的所有结点与它们相连的结点的边权中,找到边权最小的一条,如果不构成换,则将与之相连的结点加入这个集合当中。
4、重复上述操作,直至所有结点都在树中。
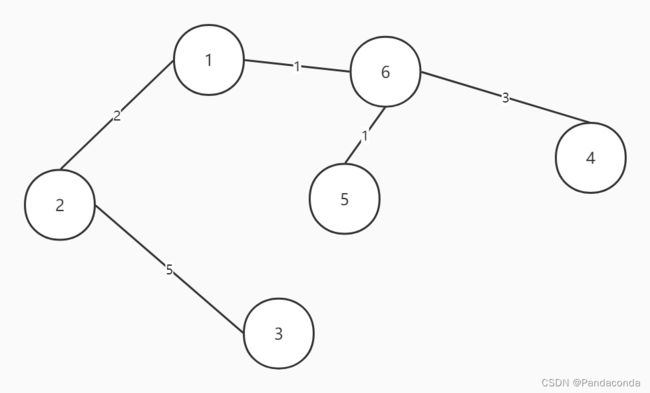
我们还是直接上图:
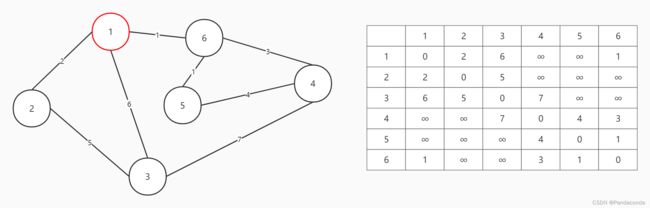
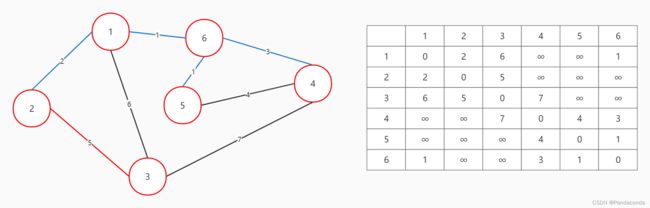
第一步:存入所有边。并且初始化集合,从结点 1 开始查找。
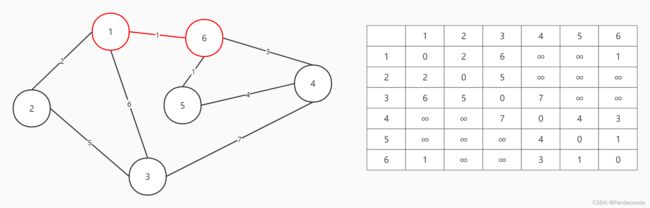
第二步:集合中相邻边权最小的是边 1 -> 6 ,将结点 6 加入集合中。
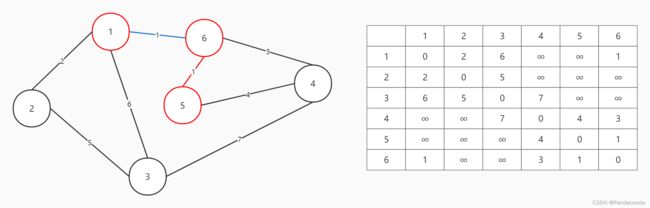
第三步:集合中相邻边权最小的是边 6 -> 5 ,将结点 5 加入集合中。
第四步:集合中相邻边权最小的是边 1 -> 2 ,将结点 2 加入集合中。
第五步:集合中相邻边权最小的是边 6 -> 4 ,将结点 4 加入集合中。
第六步:集合中相邻边权最小的是边 4 -> 5 ,但是结点 5 已经存在与集合,故舍弃该边。
第七步:集合中相邻边权最小的是边 2 -> 3 ,将结点 3 加入集合中。
至此,所有结点都已经存在与生成树中,停止遍历。
接下来我们来看看该如何实现上述操作,这里所存储边的方式是我们之前讲过的邻接矩阵,想复习的小伙伴可以跳转到之前的文章中:
图 - 01 图的概述及实现
普利姆算法相对于克鲁斯卡尔算法来说就更加的简单粗暴,直接两层循环。外面一层遍历所有结点,里面一层一方面找到外面结点到集合最短的边,另一方面更新外面结点到集合的路径,我们直接上代码。
全部代码
#include如果大家有什么问题的话,欢迎在下方评论区进行讨论哦~
【上一讲】图 - 02 图的遍历(DFS、BFS)
【下一讲】图 - 04 最短路径