子序列问题集合

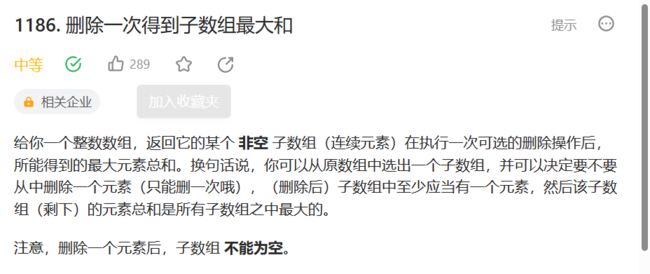
删除一次得到的最大和

class Solution {
public:
/*
left[i]：以i为结尾的子数组的最大和
right[i]：以i为开始的子数组的最大和
*/
    int maximumSum(vector<int>& arr) {
        int n=arr.size();
        vector<int> left(n),right(n);
        left[0]=arr[0],right[n-1]=arr[n-1];
        int ans=left[0];

        for(int i=1;i<n;i++)
        {
            left[i]=max(left[i-1],0)+arr[i];
            right[n-i-1]=max(right[n-i],0)+arr[n-i-1];
            ans=max(ans,left[i]);
        }

        for(int i=1;i<n-1;i++)
            ans=max(ans,left[i-1]+right[i+1]);
        return ans;
    }
    
};

最大子数组和

class Solution {
public:
/*
dp[i]：以i为结尾的连续子数组的最大和
dp的子问题定义要无后效性，同时满足题意；以i为结尾，这样能够保证
在判断i位置时，dp[i-1]是连续的，这样连上i才有意义，同时当dp[i-1]已经小于0，那么前面这些子数组就没有必要加上了，其对后面可能出现的最大子数组和没有贡献
dp[n-1]不是结果，不是最大和
*/
    int maxSubArray(vector<int>& nums) {
        int n=nums.size();
        vector<int> dp(n,0);
        dp[0]=nums[0];
        for(int i=1;i<n;i++)
        {
            if(dp[i-1]>0)
            dp[i]=dp[i-1]+nums[i];
            else
            dp[i]=nums[i];
        }
        return *max_element(dp.begin(),dp.end());
    }
};

最长公共子序列：

class Solution {
public:
	//dfs(i,j)代表s串i前字符和t串j前个字符，的公共子序列长度

	//假设最长公共子序列是lcs，则当s[i]==t[j]时，那么公共子序列长度因该是+1
	//不同时，如果s[i]在lcs中则dfs(i,j-1),  否则t[j]在lcs中则dfs(i-1,j)
	//也有可能s[i]和t[j]都不在lcs中，那么就是dfs(i-1,j-1)
	//但是显然这个能构造出来的最长公共子序列是小于上面两个的
	// int dfs(string& s,string& t,int i,int j)
	// {
	//     if(i<0||j<0)return 0;
	//     if(s[i]==t[j])
	//     return dfs(s,t,i-1,j-1)+1;
	//     else
	//     return max(dfs(s,t,i-1,j),dfs(s,t,i,j-1));
	// }
	//     int longestCommonSubsequence(string s, string t) {
	//         return dfs(s,t,s.size()-1,t.size()-1);
	//     }
	// };这样朴素的暴搜，显然会超时，并且可以很直观的发现，这里进行了很多重复的操作

	//用二维数组记录之前的结果，dfs+记忆化
	int cache[1005][1005];
	int dfs(string& s, string& t, int i, int j)
	{
		if (i < 0 || j < 0)return 0;
		int& ans = cache[i][j];
		if (ans != 0)return ans;//不为0说明已经确定过这个值了，不必dfs

		if (s[i] == t[j])
			return ans = dfs(s, t, i - 1, j - 1) + 1;
		else
			return ans = max(dfs(s, t, i - 1, j), dfs(s, t, i, j - 1));
		//return dfs(s,t,i,j);
	}
	int longestCommonSubsequence(string s, string t) {
		return dfs(s, t, s.size() - 1, t.size() - 1);
	}
};

最长上升子序列（要输出序列，和最大长度）

两种解法：

1.dp

#include
using namespace std;

/*
* 最长不下降子序列
* 1.状态描述
* dp[i]：是以i为结尾的最长不下降子序列的长度
* 2.状态转移方程
* if(a[i]>=a[j]) dp[i]=max(dp[i],dp[j]+1);
* j是i之前的元素
*/

int n, a[201], dp[201], pre[201];

void reverse_print(int index)
{
	if (index == -1)return;
	reverse_print(pre[index]);
	cout << a[index] << " ";
}

/*

14
13 7 9 16 38 24 37 18 44 19 21 22 63 15

*/

int main()
{
	memset(pre, -1, sizeof(pre));
	cin >> n;
	for (int i = 0; i < n; i++)
	{
		cin >> a[i];
		dp[i] = 1;//初始化
	}
	int maxx = 1;//最大长度至少都是1
	int maxIndex = 0;
	for (int i = 1; i < n; i++)
	{
		for (int j = 0; j < i; j++)
		{
			/*if (a[i] >= a[j])//如果只是求解序列长度，这样即可，但是要去找到这个序列，那还需要去记录其前驱
				dp[i] = max(dp[i], dp[j] + 1);
			maxx = max(maxx, dp[i]);*/

			if (a[i] >= a[j])
			{
				if (dp[j] + 1 > dp[i])//说明以j为前驱时，会得到更长的序列，此时更新pre[i]
				{
					dp[i] = dp[j] + 1;
					pre[i] = j;
				}
			}
			if (dp[i] > maxx)
			{
				maxx = dp[i];
				maxIndex = i;
			}
		}
	}
	std::cout << "max=" << maxx << endl;
	reverse_print(maxIndex);
	return 0;
}

2.贪心+二分

/*解法一：贪心+二分 */
class Solution {
public:
	int low_bound(vector<int>& arr, int key)//去找一个最小的大于key的
	{
		int left = 0, right = arr.size();

		while (left < right)
		{
			int mid = (left + right) / 2;
			if (arr[mid] < key)
				left = mid + 1;
			else if (arr[mid] > key)//当mid大于key时，不是让right=mid-1;因为有可能此时的mid就是最小的大于key的
				right = mid;
		}
		return right;
	}
	int lengthOfLIS(vector<int>& nums) {
		vector<int> ret;//ret[i]表示长度为i+1的子序列的最小值
		/*
		我尽可能让这个子序列的末尾元素小，这样后面更多的元素才可能加入
		*/
		ret.push_back(nums[0]);//一个必然升序
		for (int i = 1, k = 1; i < nums.size(); i++)//k是此时ret中有多少个元素，作为下标使用k-1
		{
			if (nums[i] > ret[k - 1])//大于ret的结尾，ret的结尾是ret中的最大的，直接加入
			{
				ret.push_back(nums[i]);
				k++;

			}
			else if (nums[i] < ret[k - 1])//遇到小于，则往前去找一个最小的并且大于的num[i]的ret
			{
				int pos = low_bound(ret, nums[i]);//这里使用二分，提高效率
				//cout << "pos=" << pos << endl;
				//if (ret[pos] == nums[i])continue;
				ret[pos] = nums[i];
			}
		}
		return ret.size();
	}
};

导弹拦截 （最长上升/下降子序列长度）

/*
* 某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷：虽然它的第一发炮弹能够到达任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。

输入导弹依次飞来的高度（雷达给出的高度数据是不大于30000的正整数，导弹数不超过1000），计算这套系统最多能拦截多少导弹，如果要拦截所有导弹最少要配备多少套这种导弹拦截系统。

389 207 155 300 299 170 158 65

6
2

其实就是去求这个序列的最长上升子序列的长度，和最长下降子序列的长度
*/

#include
using namespace std;

int n = 1, a[1001], dp_up[1001], dp_down[1001];
int main()
{
	while (cin >> a[n])
	{
		dp_up[n] = dp_down[n] = 1;
		n++;
	}
	n--;
	int max_down = 1, max_up = 1;
	for (int i = 2; i <= n; i++)
	{
		for (int j = 1; j < i; j++)
		{
			if (a[i] > a[j])dp_up[i] = max(dp_up[i], dp_up[j] + 1);
			if (a[i] <= a[j])dp_down[i] = max(dp_down[i], dp_down[j] + 1);
		}
		max_down = max(max_down, dp_down[i]);
		max_up = max(max_up, dp_up[i]);
	}
	cout << max_down << endl << max_up << endl;
	return 0;
}