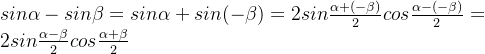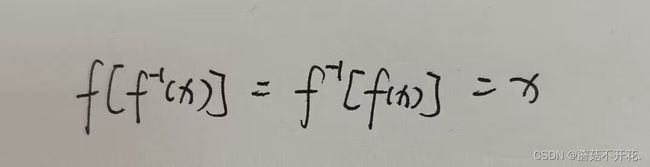高数——（反）三角函数及求导相关公式应用
为什么会有这篇文章呢？源于一道题...
，这是一道求不定积分的课后习题。当晚在求这道题时，我和我的室友先完成了以下步骤：
设
，
做到这一步之后，我们突然就不知道该这么变式了，因为需要将t变回x，而
无法操作，只能变为t才可以，但不知道该如何转换。
于是...我深深为自己的知识浅薄而感到羞愧。后来再想想，曾经也有许多题是因为忘记三角函数的相关转换公式而做不出来的，于是决定写篇文章整理一下，顺便帮助与我有同样境遇的同学~
三角函数
在开始讲公式之前，先列几个转换公式，对于我自己来说，这也是容易搞混的点。
1.三角函数转换
主要需要记住的是下面两个公式，还要熟知上面三个转换，我还见过因为没记住csc和sec而自创出别的字母的同学，高中时不需要特别注意这两点，但这些转换到了大学还是很常见的，比如在计算不定积分、定积分的题目中，后两个公式几乎天天碰到~
2.和差公式
和差公式应该可以算是高中学过的最基本的几个公式了~（因为只有这几个是我上了大学之后还记得比较牢的公式）
如果还有没记住的公式，一定要好好巩固！后面的很多公式都可以用这些基础的和差公式推导出来（tan的和差公式我的印象最深刻，若α和β中间是“+”号，则分子中间也为“+”号）。
3.万能公式
这三个万能公式，刚入大学我就忘得差不多了...第三个可以由tan的和差公式直接推导得出，但前两个我很少会用到。sin与cos万能公式的推导过程也是一样的，同时除以1，再同时除以cos，若是题目有需要，得出结论是很快的，并不需要硬背。
4.积化和差
仔细看看，其实第一个公式和第二个公式是一样的。把第二个公式转换一下，再套入第一个公式中，得出的结论其实是一样的，不过是字母换了罢了：
所以只需要记住第一个公式和第三第三两个公式就可以啦。
我是怎么记的呢？给大家分享一下我的方法，我只考虑了134三个公式：如果左边既有正弦也有余弦，那右边分子上就只有正弦；如果左边只有正弦或余弦，那右边分子上就既要有正弦也要有余弦；左边正正（正弦），右边负负（符号）；左边如果不是正正，右边都是正号；括号里都是一正一负。
5.和差化积
和差化积公式也是第一个公式和第二个公式是一样的：
所以也只需要记住134就好咯，根据134得出的记忆方法：左式中间的符号和右式的符号一致，左正弦，右正余；左（式）余弦，正（+）为余，负（-）为正。
6.求导公式
对于前四个公式只需要把它们转化成sinx和cosx就能由基础的求导公式推导啦，为了计算的方便可以记忆一下；而对于后两个，正方向的求导出现的其实不多（毕竟真的出现了也很简单！），更多的是用于倒过来告诉你右式让你求原函数，所以可以记一下右边求原函数的公式，记得求原函数的话，ln要加绝对值，即：
7.半角公式
前两个公式的推导想必大家高中都学过了，由
得出。
tan的半角公式由sin和cos的半角公式相除得出，cot则由cos半角除以sin半角，也很好得出，就是在做题是很难想到~
然后由sin和cos的半角公式相除得出tan半角公式：
之后，再通过上下同时乘
或
得出前面两个 推导公式~
文章开头的题目，就需要用到tan的半角公式！当时做题的时候如果我已经整理了这篇文章，我一定可以做出来/(ㄒoㄒ)/~~
再举个简单的例子， 
也是用到半角公式。
关于三角函数的几个公式就写这么多啦~主要是常见的一些，然后来看看反三角函数。
反三角函数
不得不说，反三角函数一直是一个重灾区，函数很常见，但高中默认大学会教，大学默认高中学过，所以大学只好重新巩固复习这一块内容：
1.定义域与值域
，定义域[-1，1]，值域[-
，]
，定义域[-1，1]，值域[0，
]
，定义域[-∞，+∞]，值域[-，]
下面是刚入大学时我关于反三角函数做的笔记：
（说到这个，穿插一个反函数的公式，想起来上次做题，标准答案用到了一个我从来没见过的公式，或许是以前学的不够细：
只要函数单调，上述公式就成立，图中公式里的“-1”代表“反函数”，而不是“负一次”，反函数关于y=x对称。）
OK，上面只是题外补充，接着继续讲反三角函数。
2.反三角函数的相互关系
反三角函数的相互关系与三角函数的相互关系之间的区别主要在于arccosx和arccotx上，因为它们不再是偶函数了，所以相互关系变成了：
，
。
3.求导公式
反函数的求导公式只需要记住arcsinx和arctanx即可，arccosx和arccotx只是加了一个负号~还是很好记忆的，只要做几道题就能记住咯
4.求原函数
求原函数其实本质就是求导的反过程嘛~但是由于这种方式在题中使用次数更多，所以就单独把这两个公式单独拿出来啦~
这篇文章就先讲到这里啦，如果有打错的公式麻烦提出来噢~（毕竟那么多公式呢，可以理解！）希望对大家有所帮助！